AP Physics Workbook 3.F Horizontal Circles
TLDRThis script discusses the physics concepts of circular motion and gravitation, particularly in the context of a police car navigating a curve. It explains how the car's speed is influenced by the radius of the curve and the coefficient of static friction between the tires and the road. The video provides a detailed breakdown of the forces acting on the car during a turn, including the centripetal force supplied by friction. It also derives an equation for the maximum safe speed a car can maintain while turning, highlighting how a decrease in friction or an increase in curve radius affects this speed. The explanation is enriched with visual descriptions and mathematical reasoning, aiming to clarify the principles for viewers.
Takeaways
- 🚓 A police car of mass M is moving at a constant speed around a horizontal curve with radius R.
- 🔄 The car is turning left and the maximum safe speed is V_nought without sliding out of control.
- 👟 The coefficient of static friction, μ_s, is the key factor between the car tires and the roadway for maintaining control.
- 📚 The scenario involves drawing a Freebody diagram to illustrate and label the forces acting on the car during the turn.
- 🧲 The force of friction is what pulls the car towards the center of the curve, providing the centripetal force.
- 🌀 The centripetal force required for circular motion is provided solely by the frictional force in this case.
- 🔢 The centripetal acceleration (a_c) is defined as V^2 / R, and the frictional force is μ * N, where N is the normal force (mg).
- 📈 A decrease in the coefficient of friction (μ) results in a lower centripetal force, thus reducing the maximum safe speed (V).
- 📊 An increase in the radius of the curve (R) allows for a higher speed due to the increased circumference that needs to be covered in the turn.
- 🔧 The maximum safe speed can be calculated using the formula V = √(μ * g * R), where g is the acceleration due to gravity.
- 🤔 Understanding the relationship between friction, radius, and speed is crucial for maintaining control and safety during turns.
Q & A
What is the scenario described in the transcript?
-The scenario involves a police car of mass M moving at a constant speed around a horizontal curve with radius R. The car is viewed as coming out of the page and turning towards the left side.
What is the maximum safe speed of the police car?
-The maximum safe speed of the police car, denoted as V_nought, is the fastest it can move without sliding out of control on the flat roadway while responding to an emergency.
What is the role of the coefficient of static friction in this scenario?
-The coefficient of static friction (mu_s) is the factor that prevents the car's tires from slipping on the roadway during the turn. It represents the friction between the tires and the road surface.
How does the force of friction relate to the centripetal force?
-The force of friction provides the centripetal force necessary for the car to follow the curved path. The centripetal force is the force that keeps the car moving in a circular path and is supplied by the friction between the tires and the road.
What happens when the coefficient of friction is less than the car's normal static friction?
-If the coefficient of friction (mu) is less than the normal static friction, the car will experience a decrease in the centripetal force, resulting in a lower maximum safe speed (V) to make the turn without losing control.
How does the radius of the curve affect the car's speed during the turn?
-A larger radius (R) means the car has to travel a longer distance to change direction by the same amount. This allows the car to go faster with the same amount of force, as it covers more distance in the same time period.
What is the mathematical expression for the maximum safe speed of the car?
-The maximum safe speed (V) can be calculated using the formula V = sqrt(mu * g * R), where mu is the coefficient of friction, g is the acceleration due to gravity, and R is the radius of the curve.
How does a decrease in the coefficient of friction (mu) affect the car's maximum safe speed?
-A decrease in the coefficient of friction (mu) results in a smaller centripetal force, which in turn reduces the maximum safe speed (V) of the car. This is because the force of friction, and thus the centripetal force, is directly proportional to mu.
How does an increase in the radius (R) of the curve affect the car's maximum safe speed?
-An increase in the radius (R) of the curve results in an increase in the maximum safe speed (V) of the car. This is because the car can cover a longer distance with the same force, allowing it to travel faster while maintaining the turn.
What is the significance of the centripetal acceleration in this context?
-Centripetal acceleration (a_c) is the acceleration that keeps the car moving in a circular path. It is defined as V^2 / R, where V is the velocity of the car and R is the radius of the curve. The centripetal acceleration is crucial for maintaining the circular motion of the car around the curve.
What is the relationship between the normal force and the force of friction?
-The normal force is the force exerted perpendicular to the surface that supports the weight of the car (mg). The force of friction is the product of the coefficient of friction (mu) and the normal force (mu * N). This frictional force is what provides the necessary centripetal force for the car to turn.
Outlines
🚓 Physics of a Police Car's Circular Motion
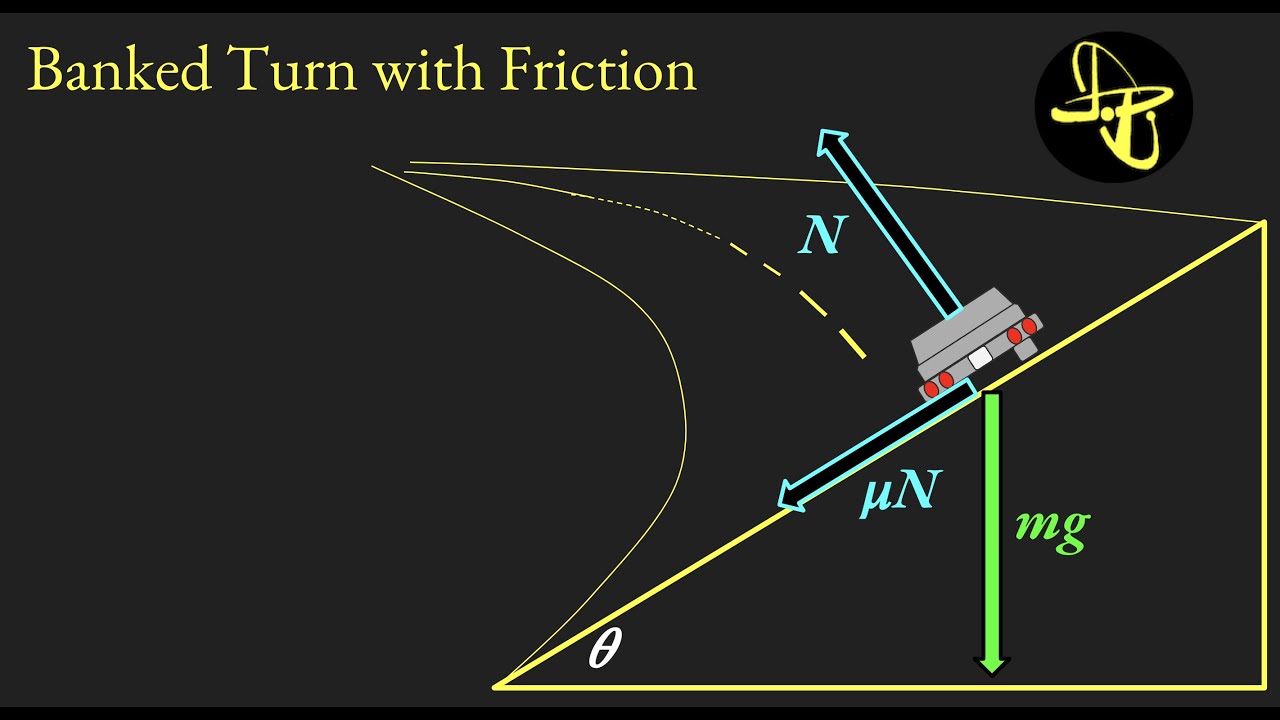
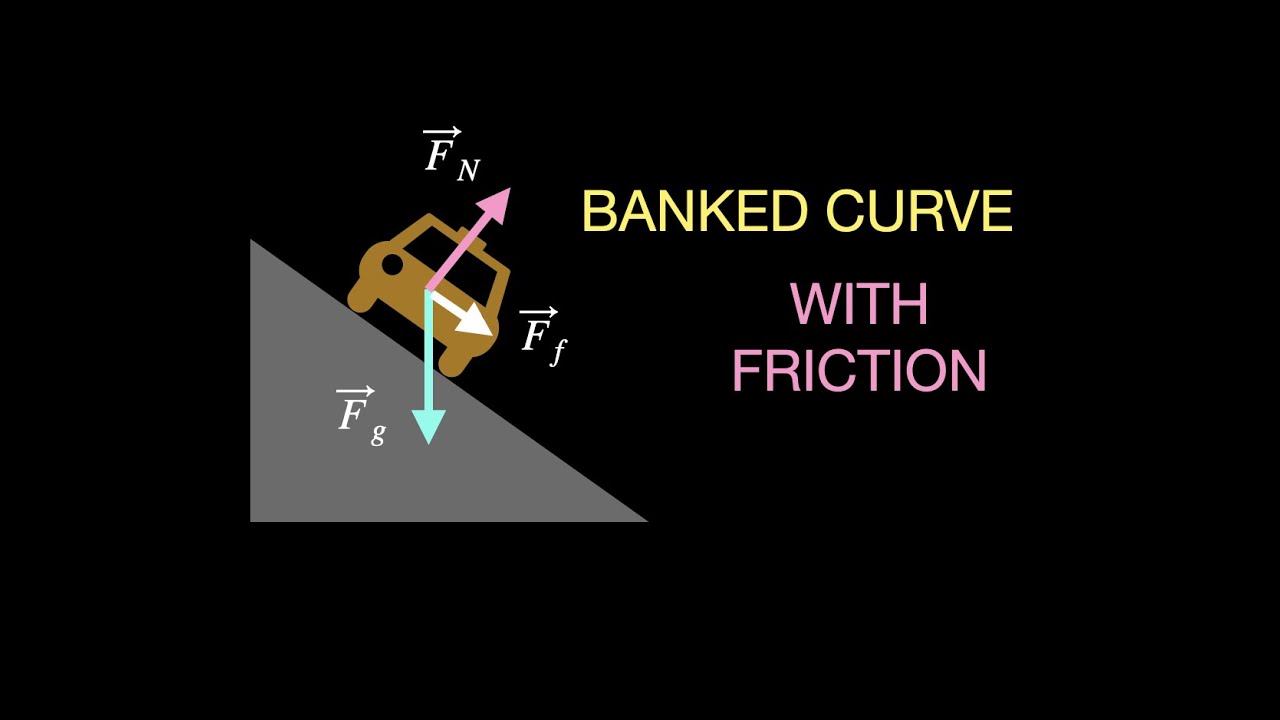
This paragraph introduces the scenario of a police car moving with constant speed around a horizontal circle. The car's mass is M, and it's turning left on a flat roadway at its maximum safe speed, Vnought, without sliding. The coefficient of static friction, mu_s, is given as the friction between the tires and the road. The paragraph describes the need to draw a Freebody diagram to illustrate and label the forces acting on the car during the turn, including the force of friction which is the centripetal force in this case. It also explains that the force exerted on the car towards the center of the curve is provided by friction on a flat road.
🌧️ Impact of Reduced Friction on Safe Speed
The second paragraph discusses a situation where the police car encounters a wet section of the road with a reduced coefficient of friction, mu. It explains how this reduction affects the maximum safe speed of the car, making it necessary to mark the new velocity, which would be less than the original due to the decreased friction force. The paragraph emphasizes understanding how the change in friction affects the car's velocity when making the turn.
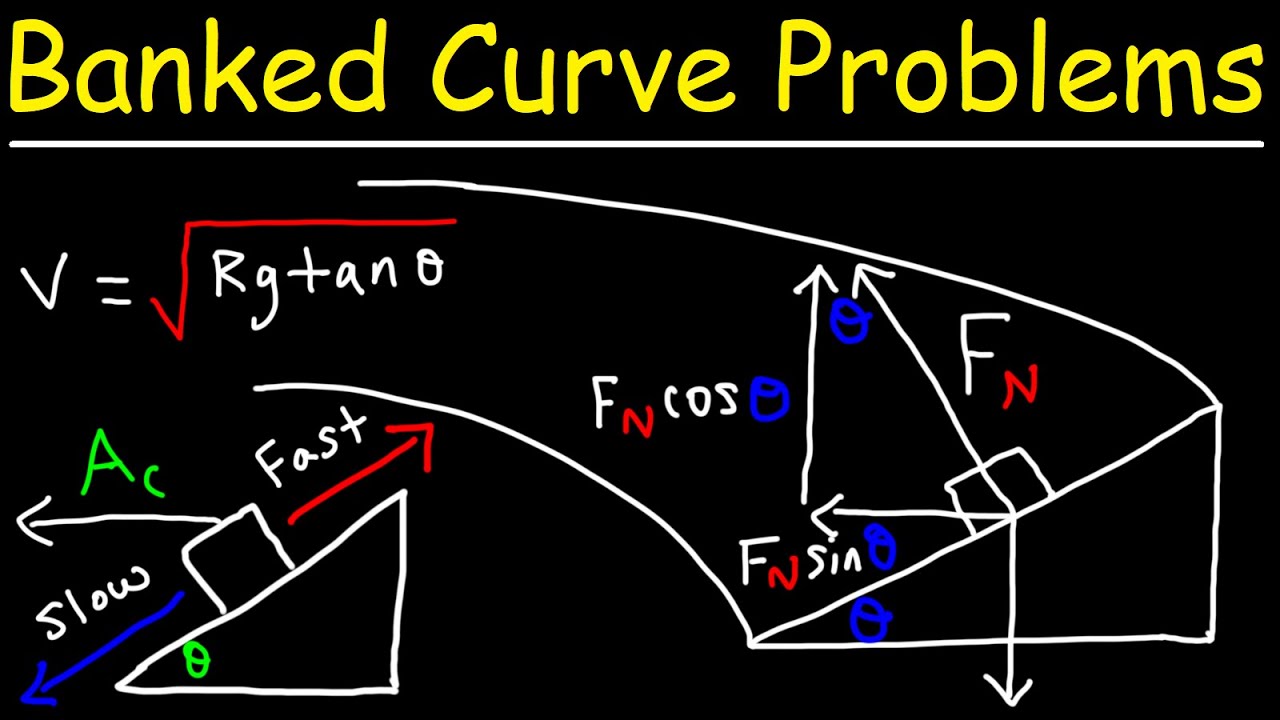
📏 Relationship Between Curve Radius and Car Speed
This paragraph explores how the radius of the curve affects the car's speed during a turn. It explains that with a larger radius, the car must travel a greater distance, and thus can go faster with the same amount of force. The key point is that the car's velocity is directly related to the radius of the curve when taking the turn with the same force. The paragraph also begins to derive an expression for the maximum safe speed of the car when turning, starting with the equation for centripetal acceleration and the force of friction.
📝 Derivation of Maximum Safe Speed Equation
The fourth paragraph details the mathematical derivation of the equation for the maximum safe speed of a car while turning. It starts with the formula for centripetal acceleration (V^2/R) and the force of friction (mu * N), where N is the normal force (mg). The paragraph walks through the algebraic steps to isolate V, resulting in the equation V = sqrt(mu * g * R). This equation shows the direct relationship between velocity, friction coefficient, gravitational force, and radius of the curve.
🔢 Effects of Friction Coefficient and Radius on Velocity
The final paragraph ties together the effects of the friction coefficient (mu) and the radius of the curve (R) on the car's velocity. It explains how a smaller mu results in a smaller velocity due to the reduced centripetal force needed. Conversely, an increase in the radius R allows for a higher velocity because the car has to cover a greater distance with the same force. The paragraph concludes by summarizing the solutions for the section, reinforcing the understanding of the physics involved in a car's circular motion and the factors affecting its safe speed.
Mindmap
Keywords
💡Circular Motion
💡Centripetal Force
💡Coefficient of Static Friction
💡Maximum Safe Speed
💡Freebody Diagram
💡Radius of Curvature
💡Friction
💡Normal Force
💡Acceleration
💡Velocity
Highlights
The scenario involves a police car moving with a constant speed around a horizontal curve.
The police car's maximum safe speed is denoted as V_nought, determined by the coefficient of static friction between the tires and the roadway.
A Freebody diagram is required to represent and label the forces exerted on the car around the corner, ensuring correct proportions.
Three forces act on the car during the turn: the force of friction, the normal force, and the gravitational force.
The force of friction is responsible for pulling the car towards the center of the curve, providing the centripetal force.
The centripetal force is the sum of certain forces, in this case, it is solely the friction force.
A decrease in the coefficient of friction (mu_s) results in a decrease in the centripetal force and thus a lower maximum safe speed (V).
When the car encounters a wet section of the road with a lower coefficient of friction, the maximum safe speed must be adjusted accordingly.
The relationship between the radius of the curve and the car's speed is such that a larger radius allows for a higher speed due to the increased distance traveled.
The equation for the maximum safe speed is derived as V = sqrt(mu * g * R), where mu is the coefficient of friction, g is the acceleration due to gravity, and R is the radius of the curve.
The force exerted on the car towards the center of the curve is provided by the friction between the tires and the pavement.
The friction force depends on the coefficient of static friction (mu) and the normal force (N), which is equal to the mass (M) times the acceleration due to gravity (g).
The car's speed must increase when turning with a larger radius to cover the longer distance in the same amount of time.
The centripetal acceleration (a_c) is defined as V^2 / R, where V is the velocity and R is the radius of the curve.
The maximum safe speed is influenced by the car's ability to maintain traction on the road, which is determined by the friction between the tires and the surface.
The car's velocity will be less than the original when the coefficient of friction is reduced, indicating a need to slow down to maintain safety.
The car's velocity will be greater than the original when the radius of the curve is increased, allowing for a higher speed without losing control.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: