Banked Curve Physics - Uniform Circular Motion
TLDRIn this educational video, Physics Ninja explores the concept of banked curves and their application in uniform circular motion, specifically in the context of cars navigating race tracks. The video simplifies the problem by neglecting friction and focuses on the forces acting on a car, such as gravity and the normal force from the road. By using Newton's second law and trigonometry, the video calculates the safe speed at which cars can take a turn on a banked curve without skidding. An example calculation is provided using the Talladega racetrack's data, revealing that cars can reach speeds of over 100 mph on a 33-degree banked curve, even without friction.
Takeaways
- 🔄 The video discusses a physics problem involving uniform circular motion and banked curves, specifically how cars navigate these without friction.
- 🛣️ A banked curve is a roadway inclined at an angle (theta) to the horizontal, designed to facilitate higher speeds around turns.
- 🚗 The problem simplifies by neglecting friction, showing that a banked angle alone can allow a car to navigate a turn at constant speed.
- 📐 The car's motion is characterized by a constant speed (V), but its velocity vector changes direction as it moves in a circle, indicating a centripetal acceleration towards the center.
- 📚 A free body diagram is used to visualize the forces acting on the car: gravitational force (weight) and the normal force from the road.
- 📏 The choice of coordinate system is crucial, with one axis aligned with the direction of centripetal acceleration for simplicity.
- 🔍 Forces are broken down into components along the chosen axes, with the normal force having both vertical (NY) and horizontal (NX) components.
- ⚖️ Newton's second law is applied to find the relationship between the normal force components, mass, acceleration, and the radius of the circular path.
- 🔢 The equations derived from Newton's laws allow for the calculation of the safe speed a car can take around a banked curve without relying on friction.
- 🏎️ An example calculation is performed using data from Talladega racetrack, illustrating how to compute the speed at which cars can navigate a banked turn.
- 📉 The video concludes with a numerical example that shows cars can reach speeds of over 100 mph on a banked curve without friction, and that actual race speeds are higher due to additional frictional forces.
Q & A
What is the main topic of the video?
-The main topic of the video is the physics of banked curves, specifically how cars navigate banked turns without the need for friction.
What does the term 'banked curve' refer to?
-A 'banked curve' refers to a road or track that is inclined at an angle (theta) with respect to the horizontal, allowing vehicles to navigate turns more efficiently.
Why does the video neglect the forces of friction?
-The video neglects the forces of friction to simplify the problem and demonstrate that cars can navigate banked turns without friction, as long as the road is banked at the correct angle.
What is uniform circular motion?
-Uniform circular motion is a type of motion where an object moves in a circular path at a constant speed, meaning the magnitude of the velocity remains constant, though its direction changes continuously.
What is the significance of the angle theta in the banked curve problem?
-The angle theta is the angle the road makes with the horizontal, which is crucial in determining the forces acting on a car and how it navigates the turn.
What is the role of the normal force in the banked curve scenario?
-The normal force is the force exerted by the road on the car's tires, which can be broken down into components that contribute to the centripetal force needed for circular motion.
How does the video determine the appropriate coordinate system for the banked curve problem?
-The video chooses a coordinate system where one axis aligns with the direction of the centripetal acceleration (toward the center of the circle), making it easier to analyze the forces acting on the car.
What is the formula for centripetal acceleration?
-The formula for centripetal acceleration (AC) is given by AC = V^2 / R, where V is the constant speed of the car and R is the radius of the circular path.
How does the video use Newton's second law to solve the banked curve problem?
-The video applies Newton's second law by setting the net force in the x-direction (toward the center of the circle) equal to the mass of the car times the centripetal acceleration.
What is the significance of the tangent of angle theta in the final speed calculation?
-The tangent of angle theta (tan(theta)) is used to relate the component of the normal force acting towards the center of the circle to the weight of the car, which is crucial in determining the safe speed for navigating the turn.
Can you provide an example calculation from the video for the Talladega racetrack?
-Yes, using the radius of approximately 1,100 feet (converted to 335.28 meters) and a bank angle of 33 degrees, the video calculates a safe speed of approximately 103.1 miles per hour without the need for friction.
Outlines
🚗 Introduction to Banked Curve Physics
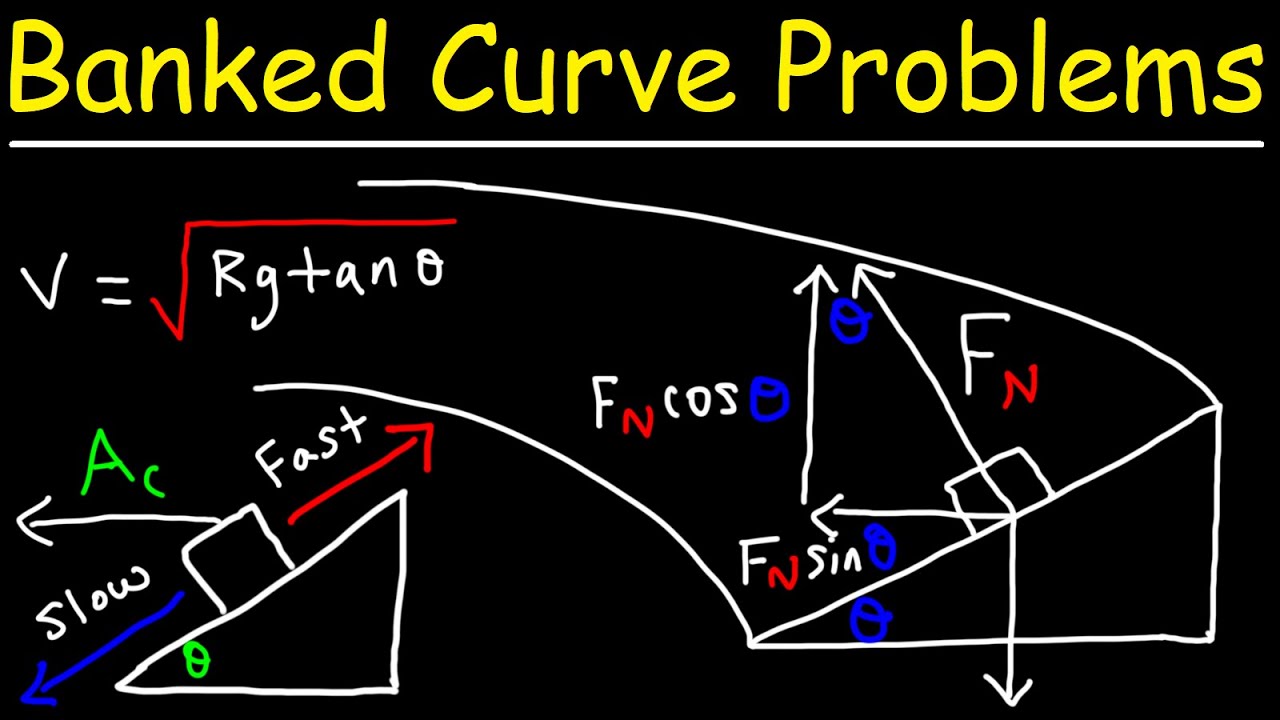
This paragraph introduces the concept of a banked curve in the context of physics, specifically uniform circular motion. The speaker, Physics Ninja, sets up the scenario of a car navigating a banked curve, which is a road inclined at an angle (theta) to the horizontal. The forces acting on the car, such as weight (W) and the normal force from the road, are discussed. The importance of choosing the right coordinate system for analyzing the forces is highlighted, and the speaker decides on a system where one axis aligns with the direction of centripetal acceleration towards the center of the circular path. The paragraph emphasizes that friction is not necessary for a car to navigate a banked turn, as long as the road is banked correctly.
📚 Analyzing Forces on a Banked Curve
In this paragraph, the speaker delves deeper into the forces acting on a car as it travels around a banked curve. The weight of the car is represented by the force W = mg, acting vertically downwards. The normal force from the road is broken down into two components: one vertical (n_y) and one horizontal (n_x), which contributes to the centripetal force required for circular motion. The speaker uses trigonometric relationships to express these components in terms of the angle theta. Newton's second law is then applied to set up equations for the forces in the horizontal and vertical directions, leading to two key equations that relate the normal force, the car's mass, the velocity, and the radius of the curve.
🔍 Calculating Speed on a Banked Curve
The speaker proceeds to calculate the speed at which a car can safely navigate a banked curve without the need for friction. By eliminating the normal force from the equations derived in the previous paragraph, an expression for the speed (V) is derived in terms of the gravitational acceleration (g), the radius of the curve (R), and the tangent of the angle theta. The importance of the angle theta and the radius R in determining the speed is discussed, with examples of how these factors affect the speed at which a car can take a turn. The paragraph concludes with a numerical example using data from the Talladega racetrack, where the radius and angle of a banked curve are used to calculate the safe speed in meters per second.
🏎️ Converting Speed to Miles per Hour
In the final paragraph, the speaker converts the calculated speed from meters per second to miles per hour to provide a more intuitive understanding of how fast the car can safely navigate the banked curve. The conversion factors for meters to miles and seconds to hours are applied to the speed calculated in the previous paragraph. The result is an approximate speed of 103.1 miles per hour, which is noted to be quite fast. The speaker also mentions that in reality, cars can go faster than this due to the additional force of friction between the tires and the road. The paragraph ends with a teaser for the next video, where the effects of friction will be included in the analysis.
Mindmap
Keywords
💡Bank curve
💡Uniform circular motion
💡Friction
💡Free body diagram
💡Normal force
💡Centripetal acceleration
💡Coordinate system
💡Newton's second law
💡Tangential velocity
💡Talladega racetrack
Highlights
Introduction to the banked curve physics problem involving uniform circular motion.
Explanation of the bank curve and its angle theta with respect to the horizontal.
Assumption of no friction in the problem for simplicity.
Description of uniform circular motion with constant speed but changing velocity.
Setting up a free body diagram for the car going around the banked curve.
Identification of forces acting on the car: weight and normal force.
Different views of the car's trajectory and the importance of centripetal acceleration.
Choosing an appropriate coordinate system aligned with the direction of acceleration.
Breaking down forces into x and y components for Newton's laws application.
Equation development for forces in the x-direction toward the center of the circle.
Use of centripetal acceleration formula in Newton's second law.
Derivation of the equation relating normal force, weight, and angle theta.
Combining equations to eliminate normal force and solve for speed.
Calculation of speed using the tangent of the angle theta and track radius.
Example calculation for Talladega racetrack with a 33-degree banked curve.
Conversion of calculated speed from meters per second to miles per hour.
Conclusion on the speed cars can safely navigate a banked curve without friction.
Teaser for the next video on the effect of friction on the banked curve problem.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: