LEPT Math Majorship 2024 | Trigonometry Calculator Techniques
TLDRThis educational video script offers an in-depth exploration of trigonometry, focusing on the fundamental concepts and their practical applications. It introduces the three primary trigonometric functions: sine, cosine, and tangent, along with their reciprocals. The script guides viewers through solving various trigonometry problems using a calculator, emphasizing the importance of understanding angles in degrees and radians. It also covers the application of trigonometric identities and laws, such as the sine law and cosine law, in solving for unknown sides and angles in right-angled triangles. The video is designed to prepare students for exams like the PRC licensure exam, providing step-by-step problem-solving techniques and examples.
Takeaways
- 📚 The video is a lesson on trigonometry, focusing on the relationship between sides and angles in right-angled triangles.
- 🔢 Trigonometry is used to find missing angles or sides of triangles using trigonometric formulas, functions, or identities, with angles measured in degrees or radians.
- 📉 The video does not cover trigonometric identities but instead applies calculator techniques to solve trigonometric problems.
- 📐 The three basic trigonometric functions discussed are sine (sin), cosine (cos), and tangent (tan).
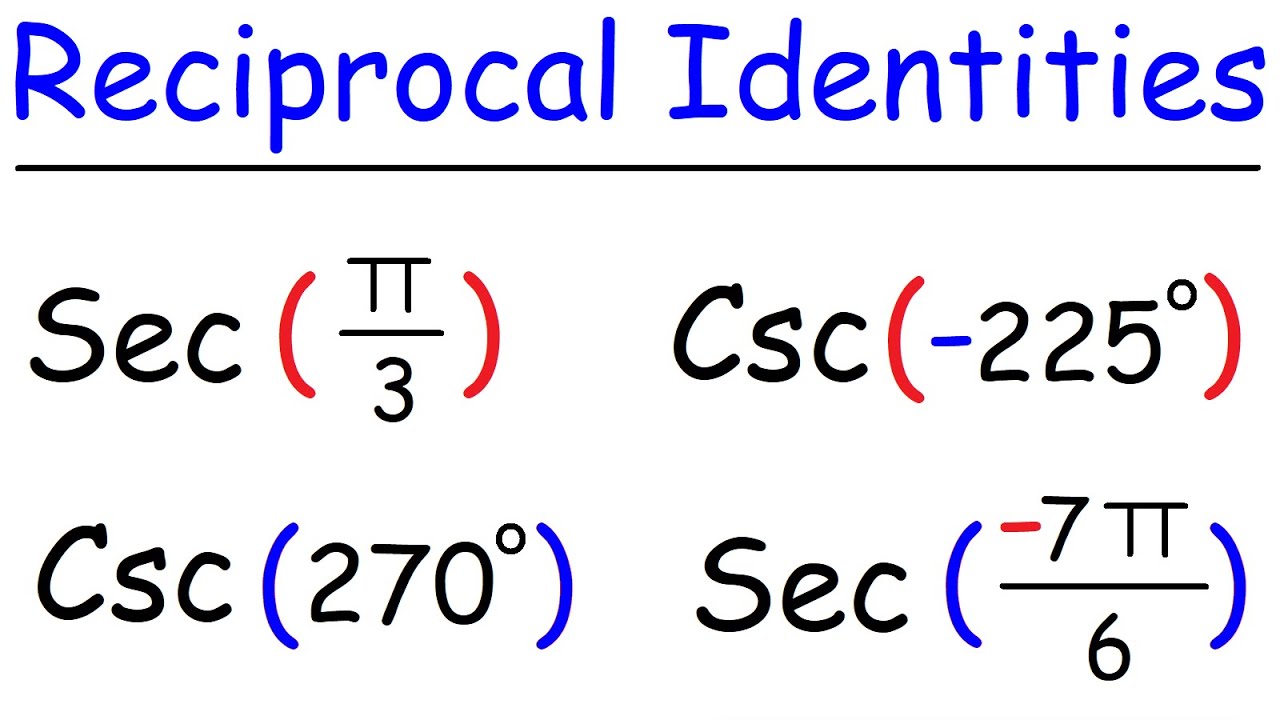
- 🔄 Reciprocals of the basic trigonometric functions are cosecant (csc), secant (sec), and cotangent (cot).
- 👨🏫 The instructor demonstrates how to use a calculator to solve for unknowns in trigonometric equations, including converting between degrees and radians.
- 📝 The video includes a series of problems that the viewers are encouraged to solve using the provided techniques and formulas.
- 🏗️ Practical applications of trigonometry are presented, such as calculating the height of a tree or a tower using angles of elevation.
- 📈 The lesson covers the use of trigonometric laws like Sine Law and Cosine Law to solve for missing sides or angles in triangles.
- 📊 The video emphasizes the importance of understanding the concepts of angles of elevation and depression in problem-solving.
- 🎓 The instructor concludes with a review of the key points covered in the lesson and encourages viewers to practice for their upcoming exams.
Q & A
What is the main topic of the video?
-The main topic of the video is trigonometry, specifically focusing on the use of a calculator to solve trigonometric problems involving right triangles.
What are the three basic trigonometric functions discussed in the video?
-The three basic trigonometric functions discussed in the video are sine (sin), cosine (cos), and tangent (tan).
What are the reciprocal trigonometric functions of sine, cosine, and tangent?
-The reciprocal trigonometric functions are cosecant (csc) for sine, secant (sec) for cosine, and cotangent (cot) for tangent.
How does the video explain the sine function in the context of a right triangle?
-The video explains the sine function as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.
What is the purpose of using a calculator in solving trigonometric problems as demonstrated in the video?
-The calculator is used to perform calculations for finding missing angles or sides of a right triangle using trigonometric formulas, especially when dealing with complex or precise values.
Can you provide an example of a problem solved in the video?
-One example problem from the video is finding the value between 270° and 360° if 2 sin^2(a) equals 1. The solution involves using the calculator to determine that the angle a is 30°, and thus the required value is 330°.
What is the significance of understanding angles in degrees and radians in trigonometry?
-Understanding angles in degrees and radians is significant because it allows for the application of trigonometric functions and formulas in various mathematical and real-world problems, depending on the given context or problem requirements.
How does the video approach the concept of angle of elevation and angle of depression?
-The video explains angle of elevation as the angle measured from the horizontal line of sight upwards towards an elevated object, while angle of depression is the angle measured downwards from the horizontal line of sight towards a lower object.
What is the Sine Law and how is it used in the video?
-The Sine Law states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all three sides of the triangle. In the video, it is used to solve for missing sides when given two angles and one side or two sides and a non-included angle.
Can you explain the Cosine Law as presented in the video?
-The Cosine Law relates the lengths of the sides of a triangle to the cosine of one of its angles. It is used when given three sides or two sides and the included angle to find the remaining side or angle.
How does the video handle word problems involving trigonometry?
-The video approaches word problems by translating the real-world scenario into a trigonometric equation, identifying the given values, and then applying the appropriate trigonometric rules or laws to solve for the unknown quantities.
Outlines
📚 Introduction to Trigonometry
The video begins with an introduction to trigonometry, a mathematical branch that studies the relationships between the sides and angles of right-angled triangles. The speaker mentions the use of a calculator, specifically the 'cash fex 570 es Plus,' for solving trigonometric problems. The focus is on finding missing angles or sides using trigonometric formulas, with angles measured in either degrees or radians. The video promises to cover basic trigonometric functions—sine, cosine, and tangent—but will not delve into trigonometric identities. An overview of these functions is provided, with sine represented as the ratio of the opposite side to the hypotenuse.
🔍 Exploring Basic Trigonometric Functions and Their Reciprocals
This paragraph delves deeper into the basic trigonometric functions: sine (sin), cosine (cos), and tangent (tan). It explains the meaning of each letter in the function names and provides the formulas for each. The reciprocals of these functions are also introduced: cosecant (csc) for sine, secant (sec) for cosine, and cotangent (cot) for tangent. The speaker emphasizes the importance of understanding these reciprocals for solving problems, especially when using a calculator, and provides examples of how to input these functions into the calculator.
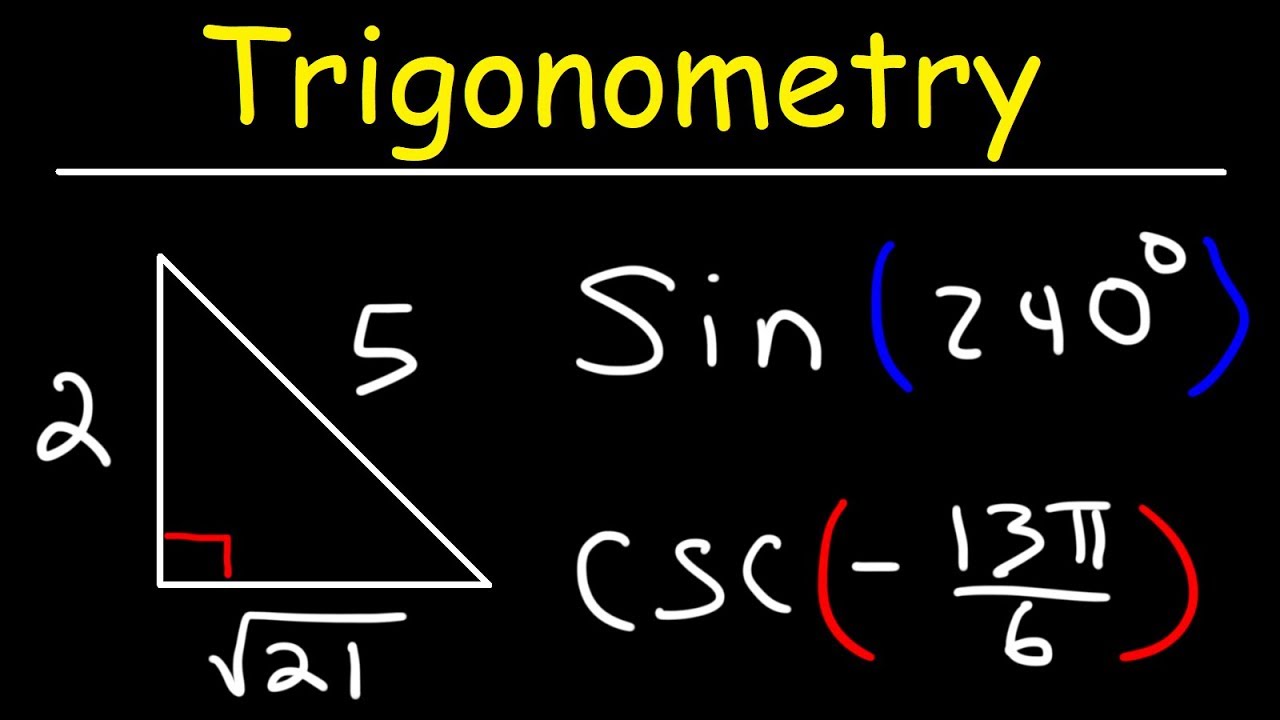
🧩 Solving Trigonometric Problems Using Calculator Techniques
The speaker presents a series of problems to solve using the calculator techniques introduced earlier. The first problem involves finding the value of an angle between 270° and 360° given a trigonometric equation. The solution process is demonstrated step by step, including how to input the equation into the calculator and interpret the results. The correct answer is identified, and the speaker encourages viewers to practice similar problems to improve their skills.
📉 Advanced Trigonometric Problem Solving
The video continues with more complex problems, such as finding the value of an angle when given the sum of cosines of two other angles. The process involves using the calculator to input and solve the equation. The speaker also presents a problem that requires simplifying a trigonometric expression, demonstrating how to use the calculator to find the simplest form of the expression. The correct answers are revealed, and the speaker provides a brief analysis of each problem.
🌳 Real-World Application: Solving for the Height of a Tree
A real-world problem is introduced where a tree breaks due to a storm, and the top touches the ground at a 30° angle with the horizontal. The distance from the base of the tree to the point where it touches the ground is given as 18 meters. The speaker uses trigonometric functions to solve for the height of the tree, demonstrating the practical application of trigonometry. The solution involves calculating the opposite and adjacent sides relative to the given angle and then combining these to find the tree's height.
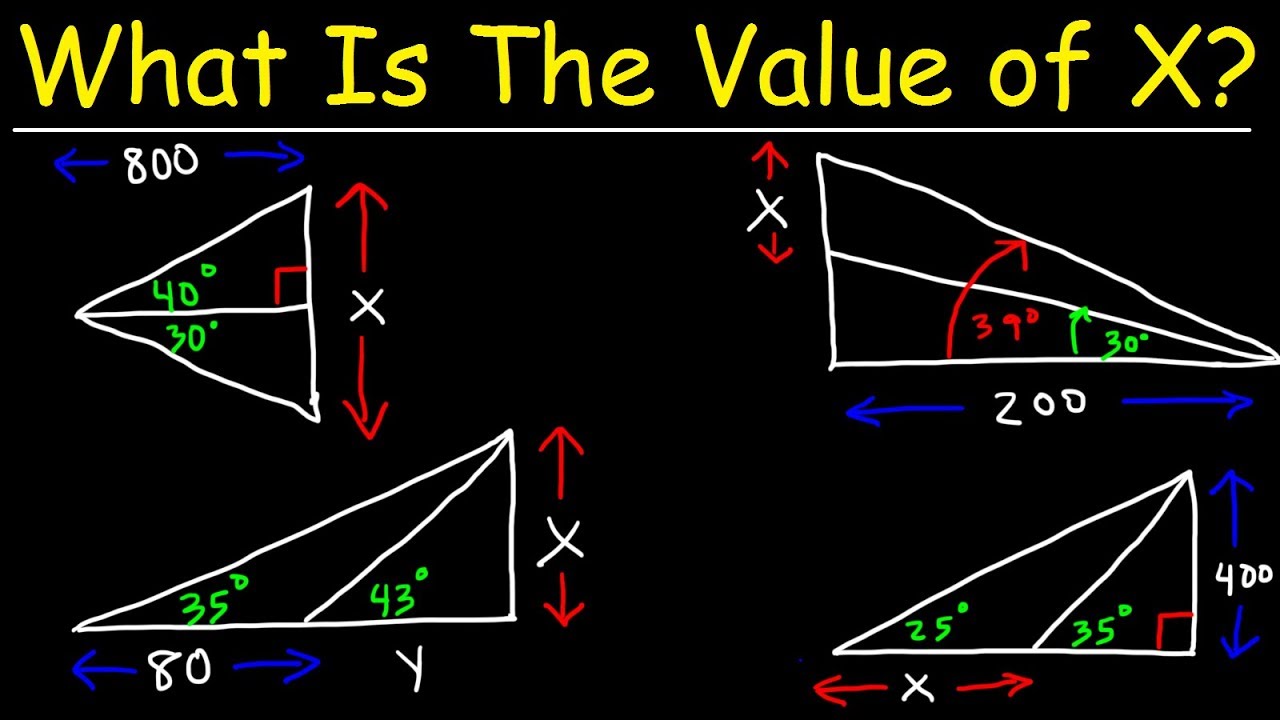
🏗️ Using Trigonometry in Triangle Problems
The video presents a problem involving a triangle with two known sides and an angle opposite one of those sides. The speaker explains how to use the sine law to find the third side of the triangle. The process involves setting up an equation based on the ratio of the sides to the sines of their opposite angles. The solution is found using a calculator, and the correct answer is identified.
📏 Solving for the Height of a Tower Using Angles of Elevation
The speaker introduces a problem where a man finds the angle of elevation of the top of a tower to be 30° and then walks 85 meters closer to the tower, finding the angle of elevation to be 60°. The goal is to find the height of the tower. The solution involves using trigonometric functions to relate the angles of elevation to the height of the tower and the distance the man walked. The correct height is calculated and presented.
📍 Determining the Length of a Pole Using Angles and Shadows
A problem involving a pole casting a 15-meter shadow with the sun at an angle of elevation of 61° is presented. The pole is also inclined 15° from the vertical towards the sun. The speaker uses trigonometric principles to determine the length of the pole. The solution process involves using the sine and cosine laws to relate the given angles and side lengths, leading to the calculation of the pole's length.
🏛️ Calculating the Height of a Monument Using Angles of Depression
The final problem involves calculating the height of a monument when the angles of depression from the top of a 50-meter tall PLT tower are given as 13° and 35°. The speaker explains how to use trigonometric functions to relate these angles to the heights of the tower and the monument. The solution involves setting up equations based on the tangent of the angles and solving for the unknown height of the monument.
📘 Review of Trigonometric Concepts and Laws
The video concludes with a review of the key trigonometric concepts and laws covered, including the three basic trigonometric functions (sine, cosine, tangent), their reciprocals, and the use of calculator techniques for solving problems. The speaker also recaps the sine law and cosine law, explaining when to apply each law based on the given sides and angles of triangles. The importance of understanding angles of elevation and depression is emphasized, as well as the practical applications of these concepts in solving real-world problems.
🙏 Closing Remarks and Future Wishes
In the closing segment, the speaker offers prayers for blessings and success in the upcoming licensure exam in 2024. They encourage viewers to share the video and express gratitude to the teachers involved in the video's creation. The speaker also includes a musical element, adding a positive and hopeful tone to the conclusion of the video.
Mindmap
Keywords
💡Trigonometry
💡Trigonometric Functions
💡Right Angle Triangle
💡Degrees and Radians
💡Reciprocals
💡Calculator Techniques
💡Sine Function (sin)
💡Cosine Function (cos)
💡Tangent Function (tan)
💡Law of Sines
💡Law of Cosines
Highlights
Introduction to the topic of trigonometry and its application in finding missing angles or sides of right triangles.
Explanation of trigonometry's relevance using a calculator, specifically the Cash fex 570 es Plus.
Clarification on the non-inclusion of trigonometric identities in the discussion due to the focus on calculator techniques.
Overview of the three basic trigonometric functions: sine, cosine, and tangent.
Definition and explanation of the sine function (sin) in the context of a right triangle.
Illustration of the cosine function (cos) and its relation to the adjacent side of a right triangle.
Discussion of the tangent function (tan) and its formula involving the opposite and adjacent sides.
Introduction of reciprocal trigonometric functions: cosecant (csc), secant (sec), and cotangent (cot).
Instruction on how to use the calculator to find reciprocal functions using 1/sin, 1/cos, and 1/tan.
Problem-solving approach for finding the value of an angle between 270° and 360° using trigonometric functions.
Method to solve for an unknown angle (Theta) when given the sum of cosines of two known angles.
Technique to simplify trigonometric expressions using reciprocal functions and calculator input methods.
Solution to a word problem involving the height of a tree broken by a storm, using tangent function.
Application of sine law in a triangle problem with given sides and a non-included angle to find the missing side.
Use of cosine law to find the third side of a triangle when two sides and the included angle are known.
Word problem involving the height of a tower, where a man changes position and observes different angles of elevation.
Problem-solving strategy for determining the length of a pole given the angle of elevation and the length of the shadow.
Method to find the height of a monument using angles of depression from a PLT Tower of known height.
Review of trigonometric functions, their reciprocals, and the application of sine and cosine laws in problem-solving.
Explanation of angles of elevation and depression in the context of real-world problem-solving scenarios.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: