Trig Identities

The Organic Chemistry Tutor

5 Apr 202327:56

EducationalLearning

32 Likes 10 Comments

TLDRThis comprehensive video script offers an in-depth exploration of trigonometric identities, essential for students embarking on a trigonometry course or preparing for final exams. It begins with the fundamental trigonometric ratios associated with a right triangle, introducing the SOHCAHTOA mnemonic to remember the sine, cosine, and tangent relationships. The script then delves into reciprocal and quotient identities, exemplified through a 3-4-5 right triangle, and continues with Pythagorean identities, highlighting the interplay between sine and cosine squared summing to one. The discussion encompasses even and odd functions, cofunction identities, and the significance of angles summing to 90 degrees. The video also covers double and half-angle identities, sum and difference formulas, power reducing formulas, and product-to-sum formulas, providing a solid foundation for advanced trigonometric concepts. It concludes with the Law of Sines, Law of Cosines, Heron's formula for calculating triangle areas, and a brief mention of the less common Law of Tangents. The script is a valuable resource for mastering trigonometric principles and solving a variety of trigonometric problems.

Takeaways

📐 **Basic Trigonometric Ratios**: The sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent) of an angle in a right triangle are fundamental to trigonometry.
🔄 **Reciprocal Identities**: The reciprocal of sine is cosecant, of cosine is secant, and of tangent is cotangent, with the reverse also being true.
📈 **Quotient Identities**: Tangent is the quotient of sine and cosine, and cotangent is the quotient of cosine and sine.
📐 **Pythagorean Identities**: The sum of the squares of sine and cosine equals one, leading to other derived identities involving cotangent and cosecant, as well as secant and tangent.
⚖️ **Even and Odd Functions**: Sine and tangent are odd functions, while cosine and secant are even functions, with cosecant and cotangent also being odd.
🔄 **Cofunction Identities**: The cofunction relationships between sine and cosine, secant and cosecant, and tangent and cotangent, especially when angles sum to 90 degrees.
📐 **Double Angle Identities**: Formulas for sine and cosine of double angles, which are essential for simplifying expressions and solving problems.
📊 **Half Angle Identities**: Expressions for sine, cosine, and tangent at half an angle in terms of the original angle, useful for simplifying and finding values.
➕➖ **Sum and Difference Identities**: Formulas for sine, cosine, and tangent when adding or subtracting two angles, with careful attention to the signs involved.
📝 **Power Reducing Formulas**: Techniques to reduce the power of trigonometric functions, such as sine squared and cosine squared, by using double angles.
🔄 **Product to Sum Formulas**: Conversion of product of trigonometric functions into sum or difference of the same functions, which can simplify calculations.
🔢 **Sum to Product Formulas**: Transformation of sum of sines or cosines into products, which is the reverse of the product to sum formulas.
🏗️ **Law of Sines and Cosines**: These laws relate the angles and sides of a triangle and are crucial for solving for missing sides or angles in a triangle.
🔢 **Area Calculation Formulas**: Methods to calculate the area of a triangle using trigonometric functions, such as using base times height times sine of the included angle or Heron's formula.
📐 **Law of Tangents**: A less commonly used formula that relates the sides and half angles of a triangle, offering an alternative method for certain trigonometric problems.

Q & A

What is the first set of trigonometric formulas that one should be familiar with when studying trigonometry?
-The first set of trigonometric formulas to be familiar with are the three main trig ratios associated with the right triangle: sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent).
What are the reciprocal identities in trigonometry?
-The reciprocal identities are: cosecant Theta is 1 over sine Theta, secant Theta is 1 over cosine Theta, and cotangent Theta is 1 over tangent Theta.
How do you calculate the sine of a 45-45-90 right triangle?
-In a 45-45-90 right triangle, the sine of the 45-degree angle is equal to the ratio of the opposite side to the hypotenuse, which simplifies to 1/√2 or √2/2.
What is the Pythagorean identity in trigonometry?
-The Pythagorean identity states that sine squared Theta plus cosine squared Theta equals one (sin²Θ + cos²Θ = 1).
How does the sign of the angle affect the values of the trigonometric functions?
-The sign of the angle affects the trigonometric functions as follows: sine and cosecant are odd functions (change sign with negative angles), while cosine and secant are even functions (remain the same with negative angles). Tangent and cotangent are also odd functions.
What are the double angle formulas for sine and cosine?
-The double angle formulas are: sin(2Θ) = 2sin(Θ)cos(Θ), and cos(2Θ) = cos²(Θ) - sin²(Θ), which can also be written as 2cos²(Θ) - 1 or 1 - 2sin²(Θ).
What is the half angle formula for tangent?
-The half angle formula for tangent is: tan(Θ/2) = √[(1 - cos(Θ)) / (1 + cos(Θ))], which can also be expressed as (1 - cos(Θ)) / sin(Θ) or sin(Θ) / (1 + cos(Θ)).
What are the sum and difference identities for sine and cosine?
-The sum and difference identities are: sin(α ± β) = sin(α)cos(β) ± cos(α)sin(β), and cos(α ± β) = cos(α)cos(β) ∓ sin(α)sin(β).
What is the Law of Sines and how is it used?
-The Law of Sines states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all three sides of the triangle. It is used to solve triangles when given certain side lengths and angles.
How do you calculate the area of a triangle using the sine of an angle?
-The area of a triangle can be calculated using the formula: (1/2)ab * sin(C), where a and b are the lengths of two sides of the triangle, and C is the included angle.
What are the product to sum formulas and how are they used?
-The product to sum formulas convert products of trigonometric functions into sums or differences of trigonometric functions. They are used for simplifying expressions and are particularly useful in solving trigonometric equations. The formulas are: sin(A)sin(B) = (1/2)[cos(A - B) - cos(A + B)], cos(A)cos(B) = (1/2)[cos(A - B) + cos(A + B)], and sin(A)cos(B) = (1/2)[sin(A + B) + sin(A - B)].

Outlines

00:00

📚 Introduction to Trigonometric Identities

This paragraph introduces the video's focus on common trigonometric identities encountered in a typical trigonometry course. It emphasizes the importance of these formulas for both beginners and those studying for exams. The paragraph begins with a right triangle and defines the sine, cosine, and tangent ratios associated with angle Theta using the mnemonic 'sohcahtoa.' It then explains the reciprocal identities for cosecant, secant, and cotangent, and provides an example problem involving a 3-4-5 right triangle to illustrate the application of these identities.

05:00

🔍 Reciprocal and Quotient Identities

The second paragraph delves into reciprocal and quotient identities. It explains that cosecant is the reciprocal of sine, secant of cosine, and tangent is the reciprocal of cotangent. The paragraph also covers quotient identities, where tangent is defined as sine over cosine, and cotangent as cosine over sine. An example is worked through to show how these identities can be used to find the trigonometric ratios for a given triangle.

10:01

🧩 Pythagorean and Even-Odd Identities

This paragraph introduces the Pythagorean identities, which are derived from the Pythagorean theorem and relate the squares of sine and cosine to one. It also discusses the even and odd properties of trigonometric functions, explaining which functions are even (like cosine and secant) and which are odd (like sine and tangent). Cofunction identities are also covered, showing how the values of sine and cosine are related when the angles sum to 90 degrees.

15:03

🔢 Double Angle and Half Angle Identities

The fourth paragraph covers double angle and half angle identities. It provides formulas for sine and cosine of double angles, as well as the tangent of double angles. The paragraph then moves on to half angle identities, explaining how to find the sine, cosine, and tangent of half an angle using square roots and reciprocal trigonometric functions. The derivation of tangent half angle identities from their basic form is also included.

20:04

⚖️ Sum and Difference Identities

This paragraph explores sum and difference identities for sine, cosine, and tangent. It explains how to calculate the sine or cosine of the sum or difference of two angles, with attention to the signs involved. The paragraph also discusses the relationship between the signs in the formulas and how they correspond to the angle sum or difference.

25:04

📐 Power Reducing and Product to Sum Formulas

The sixth paragraph focuses on power reducing formulas, which simplify the square of trigonometric functions into a form involving double angles. It also covers product to sum formulas, which allow the conversion of product of sines and cosines into sums or differences of sines and cosines. The paragraph provides examples of how to use these formulas and directs viewers to additional resources for practice.

🏗️ Law of Sines, Cosines, and Tangents

The final paragraph discusses the Law of Sines, which relates the ratios of the sides of a triangle to the sines of its angles. It also covers the Law of Cosines, which is used when all sides of a triangle are known but the angles are not. The paragraph briefly touches on Heron's formula for calculating the area of a triangle and introduces the less commonly used Law of Tangents. The video concludes with a summary of the trigonometric identities covered and a thank you to the viewers.

Mindmap

Keywords

💡SOHCAHTOA

SOHCAHTOA is a mnemonic device used to remember the basic trigonometric ratios: Sine (opposite/hypotenuse), Cosine (adjacent/hypotenuse), and Tangent (opposite/adjacent). In the video, it's introduced to help learners understand and memorize how these ratios are calculated in relation to a right triangle. It serves as a foundational concept for students starting in trigonometry, highlighting the relationships between angles and sides in right triangles.

💡Reciprocal identities

Reciprocal identities in trigonometry refer to identities that involve the reciprocals of the sine, cosine, and tangent functions. Specifically, cosecant is the reciprocal of sine, secant is the reciprocal of cosine, and cotangent is the reciprocal of tangent. The video discusses these identities to help viewers understand that each trigonometric function has a corresponding reciprocal function, crucial for solving various trigonometric problems.

💡Pythagorean identities

The Pythagorean identities are fundamental in trigonometry, derived from the Pythagorean theorem. They include identities like sine squared plus cosine squared equals one. The video uses these identities to explain how they can simplify and solve trigonometric expressions and equations, illustrating their practical applications in different trigonometric scenarios.

💡Even and odd functions

In the video, even and odd functions are discussed in the context of trigonometric functions. An even function, like cosine, returns the same value for positive and negative inputs of the angle. An odd function, like sine and tangent, returns the negative of the function value when the input angle is negated. This distinction is crucial for understanding symmetry in trigonometric functions and impacts how these functions are manipulated in solving trigonometric equations.

💡Cofunction identities

Cofunction identities relate to functions where the sum of the angles involved equals 90 degrees (or pi/2 radians). For example, the sine of an angle is equal to the cosine of its cofunction (90 degrees minus the angle). These identities are pivotal for converting between trigonometric functions of complementary angles, simplifying expressions, and solving equations, as demonstrated in the video.

💡Double angle identities

Double angle identities provide formulas to calculate the sine, cosine, or tangent of twice an angle from the sine, cosine, or tangent of the original angle. The video explains how these identities are used to expand, simplify, or solve trigonometric expressions and equations, especially in more complex trigonometry problems.

💡Sum and difference identities

These identities allow the expression of the sine and cosine of sums or differences of angles in terms of the sines and cosines of the individual angles. The video discusses how these identities are crucial for simplifying trigonometric expressions involving the addition or subtraction of angles, and are commonly used in waveform analysis and acoustics.

💡Law of Sines

The Law of Sines relates the ratio of the length of a side of a triangle to the sine of its opposite angle. This law is essential for solving for unknown sides and angles in non-right triangles, which the video highlights as a practical tool in fields such as surveying and astronomy.

💡Law of Cosines

The Law of Cosines is used to calculate an unknown side or angle in a triangle where two sides and the included angle, or three sides, are known. The video discusses its application in solving triangles, emphasizing its utility in cases where the Law of Sines cannot be applied directly.

💡Half angle identities

Half angle identities are used to find the sine, cosine, or tangent of half an angle given the sine, cosine, or tangent of the original angle. These are especially useful in integration and in solving trigonometric equations involving powers of sine and cosine, as highlighted in the video for their role in simplifying complex trigonometric problems.

Highlights

Introduction to common trigonometric identities essential for trigonometry courses.

Explanation of SOHCAHTOA for sine, cosine, and tangent calculations.

Detailed breakdown of reciprocal identities like cosecant, secant, and cotangent.

Application of trigonometric ratios to solve for the six trigonometric ratios of a 3-4-5 right triangle.

Introduction and derivation of the Pythagorean identities from the Pythagorean theorem.

Classification of sine, cosine, and tangent as odd functions and their characteristics.

Discussion of even functions in trigonometry with examples using cosine and secant.

Exploration of cofunction identities and their significance in trigonometry.

Detailed examples of how cofunction identities like sine and cosine relate when angles sum to 90 degrees.

Introduction to double angle identities for sine, cosine, and tangent.

Explanation of half-angle identities and their different forms using algebraic manipulation.

Overview of sum and difference identities, with a focus on their practical applications in problem solving.

Details on product-to-sum and sum-to-product formulas with practical examples.

Introduction to the Law of Sines and its use in solving triangles.

Explanation of the Law of Cosines for determining unknown angles or sides in triangles.

Discussion of lesser-known trigonometric laws like the Law of Tangents.

Transcripts

Browse More Related Video

Trig - 0.4 Fundamental Trig Identities

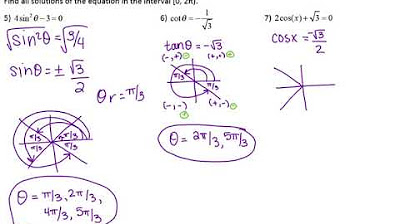
Precalc Chapter 5 Review

LEPT Math Majorship 2024 | Trigonometry Calculator Techniques

5.5 Multiple Angle and Product to Sum Formulas (Part 1)

Inverse Trig Functions With Double Angle Formulas and Half Angle Identities - Trigonometry

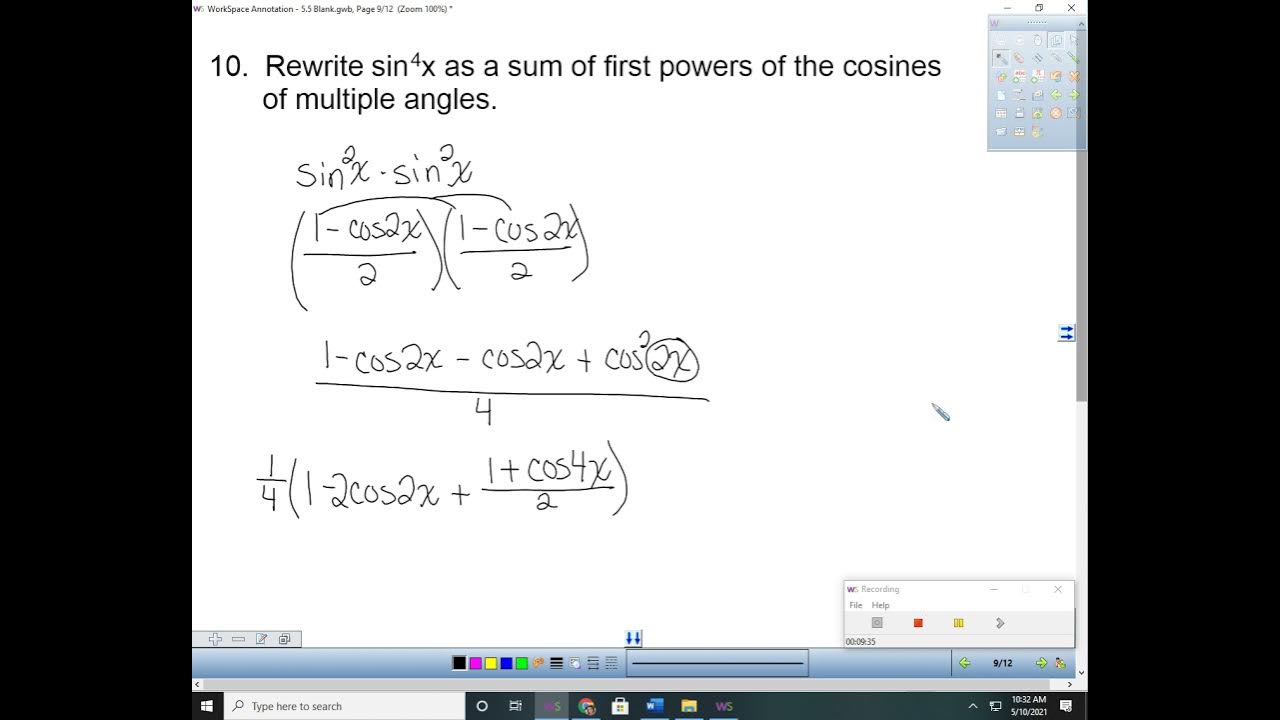
5.5 Multiple Angle and Product to Sum Formulas (Part 2)