CASIO FX 991ES PLUS - Calculator skills - differentiation

HEGARTYMATHS
24 Sept 201304:01
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Hegarty Math demonstrates the importance of using a calculator as a check method for differentiation in GCSE and A-Level mathematics. The instructor shows how to differentiate functions mathematically and then use the calculator's 'D by DX' function to verify the results. By inputting the function and a specific value for 'x', the calculator provides the derivative, which can be compared with the manually calculated result. This method ensures accuracy and builds confidence in students' understanding of differentiation. The video concludes with a reminder that while calculators are useful for checking work, they should not replace a solid grasp of mathematical concepts.

Takeaways
  • 📚 The video is aimed at GCSE and A-Level students and focuses on using a calculator as a check for differentiation.
  • 🧐 Students are reminded that understanding the mathematical process is crucial, and the calculator is only a tool for verification.
  • 🔍 The video demonstrates how to check the differentiation of a function, f(x) = 7 + 3x + 2x^2, by hand and using a calculator.
  • 📝 The differentiation of the function f(x) is shown to be 3 + 4x, which is verified by substituting x = 1/7 into the function and the derivative.
  • 🔢 The calculator is used to check the derivative by setting it to mode one and using the 'D by DX' button to differentiate the function.
  • 📈 The calculator provides a numerical answer when x = 1/7, which is then compared to the manual calculation to ensure accuracy.
  • 📉 Another example is given where the function y = 3x^5 - 4x^(-2) is differentiated to dy/dx = 15x^4 - 8/x^3.
  • ✍️ The differentiation process is explained step by step, emphasizing the importance of understanding the mathematical operations.
  • 🔧 The calculator is used again to check the differentiation of the second function by substituting x = 1/7 and comparing the result with the manual calculation.
  • 📊 The video concludes by emphasizing the calculator as a reliable method to double-check work during exams, providing confidence in the accuracy of differentiation.
  • 👍 The video ends with a thank you note for watching, summarizing the importance of using a calculator as a check for differentiation in mathematical studies.
Q & A

  • What is the main purpose of using a calculator in the context of this math video?

    -The main purpose of using a calculator in this context is to check the correctness of differentiation performed manually. It's not to rely on the calculator for the differentiation itself, but to ensure that the mathematical process and result are accurate.

  • What is the function f(x) given in the script?

    -The function f(x) given in the script is 7 + 3x + x^2.

  • How does the script suggest to check the differentiation of f(x)?

    -The script suggests setting the calculator to mode one and using the D by DX button to differentiate the function. Then, by inputting a specific value for x, such as 1/7, the calculator can provide the derivative at that point.

  • What is the derivative of f(x) if f(x) is 7 + 3x + x^2?

    -The derivative of f(x) = 7 + 3x + x^2 is f'(x) = 3 + 2x.

  • What value of x is used to check the derivative of f(x) in the script?

    -The value of x used to check the derivative of f(x) in the script is 1/7.

  • How does the script verify the manual calculation of the derivative?

    -The script verifies the manual calculation by comparing the result obtained from substituting x = 1/7 into the manually derived function f'(x) = 3 + 2x with the result given by the calculator when differentiating f(x) = 7 + 3x + x^2 at x = 1/7.

  • What is the second function Y given in the script?

    -The second function Y given in the script is 3x^5 + 4/x^2.

  • What is the derivative of Y with respect to x?

    -The derivative of Y with respect to x, if Y = 3x^5 + 4/x^2, is dy/dx = 15x^4 - 8/x^3.

  • How does the script suggest using the calculator to check the derivative of Y?

    -The script suggests inputting the derivative formula into the calculator and then substituting the value of x (1/7 in this case) to check if the result matches the manual calculation.

  • What is the result obtained from the calculator when differentiating Y at x = 1/7?

    -The result obtained from the calculator when differentiating Y at x = 1/7 is approximately -2.743.

  • What is the final message of the video regarding the use of a calculator for differentiation?

    -The final message is that the calculator serves as a useful check method to ensure the correctness of manual differentiation, providing comfort and confidence in exam situations.

Outlines
00:00
📚 Introduction to Calculator Skills in Mathematics

This paragraph introduces the video's focus on using calculators as a check method for differentiation problems in GCSE and A-Level mathematics. The speaker emphasizes the importance of understanding the mathematical process behind differentiation, rather than solely relying on the calculator. The video aims to guide viewers on how to verify their differentiation work using a calculator, ensuring accuracy in mathematical problem-solving.

🔍 Verifying Differentiation with a Calculator

The speaker demonstrates how to use a calculator to check the differentiation of a given function. They provide an example where the function f(x) is differentiated to find F'(x). The process involves manually differentiating the function and then using the calculator's differentiation function to verify the result. The video shows the step-by-step method of entering the function into the calculator, setting the variable x to a specific value, and obtaining the derivative to confirm the manual differentiation was done correctly.

📘 Calculating Derivatives and Checking with a Calculator

The paragraph continues with another example of differentiation, this time with the function Y involving powers of x. The speaker outlines the manual differentiation process and then uses the calculator to check the result. They show how to input the differentiated function into the calculator and substitute a specific value for x to obtain the derivative. The video confirms that the manual and calculator results match, providing a reliable check for the differentiation process.

📝 Conclusion on Using Calculators for Differentiation Checks

In conclusion, the speaker reiterates the importance of using calculators as a verification tool for differentiation, rather than as a primary method for solving problems. They highlight that while calculators can provide quick checks, a solid understanding of the mathematical concepts is essential for success in exams and problem-solving. The video ends with a reminder to viewers to practice both manual differentiation and calculator checks to ensure accuracy and confidence in their mathematical abilities.

Mindmap
Keywords
💡GCSE
GCSE stands for General Certificate of Secondary Education, which is a system of examinations in the United Kingdom that students typically take in their final years of secondary school. In the context of the video, it indicates that the content is tailored to students preparing for this level of education, specifically in mathematics.
💡A-level
A-level refers to Advanced Level qualifications, which are part of the secondary education system in the UK. They are taken by students after completing their GCSEs and are considered a pre-university qualification. The video mentions A-level to indicate that the material is also relevant for students studying at this advanced secondary level.
💡Calculator
In the video, the calculator is presented as a tool for checking mathematical calculations, specifically in the context of differentiation. It is not a substitute for understanding the mathematical process but serves as a useful check to ensure accuracy in calculations.
💡Differentiation
Differentiation in mathematics is the process of finding the derivative of a function, which represents the rate at which the function changes with respect to one of its variables. The video focuses on teaching and checking differentiation skills, which are crucial for students preparing for GCSE and A-level exams.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. The script discusses the differentiation of functions, such as 'f(x)' and 'y', which are represented by algebraic expressions.
💡Differential
The differential 'dF/dx' or 'dy/dx' represents the derivative of a function with respect to the variable 'x'. It is the fundamental concept that the video is exploring, showing how to calculate it both manually and using a calculator.
💡Mode
In the context of the video, 'mode' refers to the setting or function on a calculator that allows for differentiation. The script instructs viewers to set their calculator to 'mode one' to use the differentiation function, demonstrating how to switch to the appropriate mode for the task.
💡D by DX button
The 'D by DX' button on a calculator is used to perform differentiation. The video script explains how to use this button to differentiate a function that the user inputs into the calculator, providing a step-by-step guide on its usage.
💡Polynomial
A polynomial is an algebraic expression made up of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The script uses a polynomial '2x^2' as part of the function to be differentiated.
💡Substitution
Substitution in calculus is the process of replacing a variable in an expression with another value or expression. The video demonstrates how to substitute a value ('1/7') into a differentiated function to check the accuracy of the manual differentiation process.
💡Check method
The check method mentioned in the video refers to using the calculator as a way to verify the manual differentiation process. It is a technique to ensure that the mathematical work done manually is correct, providing a form of validation for the student's calculations.
Highlights

Introduction to a GCSE and A-level math video focusing on calculator skills for checking differentiation.

Emphasis on understanding mathematical processes rather than just using the calculator.

Demonstration of how to check differentiation using a calculator as a verification tool.

Explanation of the differentiation process for a given function f(x).

Step-by-step guide on differentiating a polynomial function and checking the result.

Using the calculator's 'D by DX' button to perform differentiation.

Example of inputting a function into the calculator and setting an x-value for differentiation.

Calculating the derivative at x = 1/7 and comparing it with the manual calculation.

Verification of the manual differentiation result using the calculator's output.

Introduction of a second example involving differentiation of a more complex function.

Differentiation of a function involving powers of x and negative exponents.

Using the calculator to check the differentiation result at a specific x-value.

Comparing manual and calculator results to ensure the correctness of the differentiation.

Highlighting the importance of using the calculator as a check method in exams.

Providing reassurance and confidence through the use of calculator checks.

Conclusion of the video with a summary of the importance of calculator skills in verifying differentiation.

Transcripts

Browse More Related Video

Casio FX-991EX Differentiation Tutorial: How to Find Derivatives on Your Casio Calculator

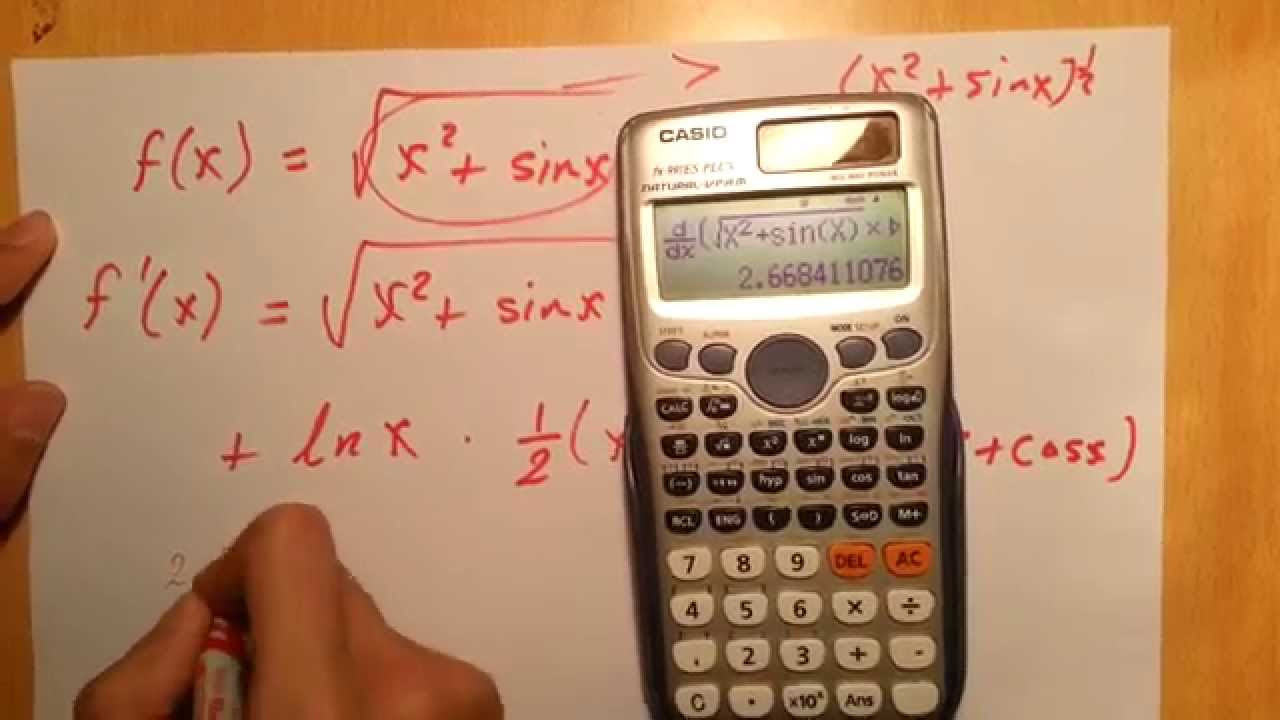
How to Differentiate using calculator

CASIO FX 991ES PLUS: Calculator skills - factorising quadratics

Lesson 3 1B Using the Calculator to find Derivatives and Critical Numbers

Derivative of absolute value function

How to solve differentiation using your calculator(Casio Cs- 991 ES plus)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Maths TutorialDifferentiationCalculator SkillsGCSE MathsA-level MathsEducational ContentExam PreparationCheck MethodMaths PracticeLearning Tools