How to Differentiate using calculator

Solvey
6 Sept 201505:16
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the host guides viewers through the process of checking the differentiation of mathematical functions using a calculator. Starting with a simple example of a quadratic function, the host demonstrates how to input the function and use the calculator's derivative function to verify the derivative at a specific value of x. The video continues with a more complex example involving a combination of square root and trigonometric functions, showing step-by-step how to correctly input and differentiate the function, and then verify the result by plugging in a value for x. The host encourages viewers to ask questions on various topics, emphasizing the video's utility for learning and problem-solving.

Takeaways
  • 🔍 The video is a tutorial on how to use a calculator to check the differentiation of mathematical functions.
  • 📚 The presenter begins with a simple example: differentiating the function f(x) = x^2 + 4x + 5, which yields the derivative 2x + 4.
  • 📱 To check the derivative on a calculator, press the shift button followed by the derivative function key.
  • 🔢 The presenter suggests using a specific value for x (e.g., x = 6) to verify the derivative by plugging it back into the original function.
  • 🧩 The video demonstrates how to check the derivative at x = 6, which should equal 16, confirming the correctness of the differentiation process.
  • 📈 Another example provided involves a more complex function: √(x^2 + sin(x)) * x^2, with a derivative that combines both multiplication and chain rules.
  • 🔍 The derivative of the second example is calculated as (1/2x) * (x^2 + sin(x)) + sin(x) * (2x + cos(x)) and is checked using a calculator.
  • 📝 The presenter emphasizes the importance of correctly inputting the function into the calculator, paying attention to brackets and functions.
  • 🔢 The video shows the process of checking the derivative at x = 5, which results in a value of 2.668, matching the manually calculated derivative.
  • 👨‍🏫 The presenter encourages viewers to ask questions related to various subjects, including mathematics, physics, electronics, and more.
  • 👍 The video concludes with a call to action for viewers to subscribe, like, and comment with any questions they might have.
Q & A

  • What is the purpose of the video?

    -The purpose of the video is to demonstrate how to use a calculator to check the differentiation of mathematical functions.

  • What is the first function given in the video as an example for differentiation?

    -The first function given in the video is f(x) = x^2 + 4x + 5.

  • What is the derivative of the function f(x) = x^2 + 4x + 5?

    -The derivative of the function f(x) = x^2 + 4x + 5 is 2x + 4.

  • How does the video suggest checking the derivative using a calculator?

    -The video suggests checking the derivative by entering the function into the calculator, setting a value for x, and then comparing the calculator's output with the manually calculated derivative at that value.

  • What value of x is used in the video to check the derivative of the first function?

    -The value of x used in the video to check the derivative of the first function is 6.

  • What is the result of the derivative when x equals 6 for the first function?

    -The result of the derivative when x equals 6 for the first function is 16.

  • What is the second function given in the video as an example for differentiation?

    -The second function given in the video is √(x^2 + sin(x)) * ln(x).

  • How does the video explain the process of differentiating the second function?

    -The video explains that the derivative of the second function involves using the product rule, multiplying the derivative of the first part by the second part and vice versa, and being careful with the brackets.

  • What value of x is used in the video to check the derivative of the second function?

    -The value of x used in the video to check the derivative of the second function is 5.

  • What is the result of the derivative when x equals 5 for the second function?

    -The result of the derivative when x equals 5 for the second function is approximately 2.668.

  • What are the additional subjects mentioned in the video that viewers can ask questions about?

    -The additional subjects mentioned in the video for viewers to ask questions about include mathematics, physics, electronics, circuits, speech communication, and puzzles.

Outlines
00:00
📚 Checking Derivatives with a Calculator

This paragraph introduces a tutorial video on how to verify the differentiation of mathematical functions using a calculator. The presenter demonstrates the process by first differentiating a simple quadratic function, f(x) = x^2 + 4x + 5, and showing that the derivative is 2x + 4. To verify the result, the presenter plugs in x = 6 into the derivative and confirms it equals 16, which matches the manual calculation. The video continues with a more complex example involving a function that combines a square root and a sine function, and the presenter explains the derivative step by step, emphasizing the importance of correctly handling brackets and functions within them. The presenter then uses the calculator to check the derivative at x = 5, showing the process of inputting the function and verifying the result, which matches the expected value of 2.668.

05:00
📢 Engaging with the Audience for Future Content

In the concluding paragraph, the presenter invites viewers to engage with the content by subscribing to the channel and leaving comments with any questions they may have. The video covers a range of topics including mathematics, physics, electronics, circuits, speech communication, and even puzzles. The presenter expresses a desire to address these questions in future videos, encouraging a two-way interaction with the audience to tailor the content to their interests and needs.

Mindmap
Keywords
💡Differentiation
Differentiation in the context of the video refers to the mathematical process of finding the derivative of a function with respect to a variable. It is a fundamental concept in calculus and is used to analyze the rate at which a quantity changes. In the video, differentiation is the main theme, as the host demonstrates how to use a calculator to differentiate functions such as 'f(x) = x^2 + 4x + 5' and 'f(x) = sqrt(x^2) + sin(x) * ln(x)'.
💡Calculator
A calculator is an electronic device used for performing arithmetic operations and more complex calculations. In the video, the calculator is used as a tool to check the differentiation of mathematical functions. The host explains the process of using specific calculator functions to find the derivative of given functions, which is essential for verifying the correctness of manual differentiation.
💡Derivative
The derivative is a measure of how a function changes as its input changes. It is the slope of the tangent line to the function's graph at a particular point. In the video, the host uses the term 'derivative' to refer to the result of differentiating a function, such as finding that the derivative of 'x^2 + 4x + 5' is '2x + 4'.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. In the video, functions are represented by expressions like 'f(x) = x^2 + 4x + 5' and 'f(x) = sqrt(x^2) + sin(x) * ln(x)', which the host differentiates to demonstrate the process.
💡Shift Button
The shift button on a calculator is typically used to access additional functions or modes. In the video, the host instructs the viewers to press the shift button to access the derivative function on the calculator, which is necessary for the differentiation process being demonstrated.
💡Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. In the video, the square root function is part of the second example function 'f(x) = sqrt(x^2) + sin(x) * ln(x)', where the host differentiates the function and checks the result using a calculator.
💡Sine Function
The sine function is a trigonometric function of an angle, usually in a right-angled triangle, and is represented as 'sin(x)'. In the video, the sine function is used in the second example function, and its derivative is part of the final differentiated expression.
💡Natural Logarithm
The natural logarithm, denoted as 'ln(x)', is the logarithm of a number to the base 'e', where 'e' is an irrational constant approximately equal to 2.71828. In the video, the natural logarithm is part of the second example function, and its derivative is calculated as part of the differentiation process.
💡Brackets
Brackets in mathematics are used to group terms or expressions together, often to indicate that operations within the brackets should be performed first. In the video, the host emphasizes the importance of being careful with brackets when entering functions into the calculator to ensure the correct differentiation.
💡Radian
A radian is a unit of angular measure used in trigonometry, defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. In the video, the host mentions ensuring that calculations are done in radian form when differentiating functions involving trigonometric functions like sine.
💡Check
In the context of the video, 'check' refers to the process of verifying the correctness of the calculated derivative by substituting a specific value of 'x' into the original function and comparing it with the derivative function. The host demonstrates this by checking the derivative of 'x^2 + 4x + 5' at 'x = 6' and finding it to be 16, which matches the manual calculation.
Highlights

Introduction to a new episode from the 'soggy' series where viewers' questions are answered in videos.

Demonstration of how to check differentiation using calculators.

Example given: Differentiating the function f(x) = x^2 + 4x + 5.

Explanation of the straightforward answer to the example: 2x + 4.

Guide on using the calculator to check the derivative: Press shift and the derivative button.

Process of entering the function into the calculator for differentiation.

Using a specific number (e.g., 6) to evaluate the derivative of the function.

Verification of the calculator's answer by plugging the number back into the original function.

Confirmation of the correct differentiation process through the example.

Introduction of a second example involving a more complex function.

Explanation of the derivative for a complex function involving square root and sine.

Detailed breakdown of the derivative calculation using the product and chain rules.

Instructions on using the calculator for the complex function, emphasizing careful bracketing.

Use of the number 5 to evaluate the derivative of the complex function.

Emphasizing the importance of using radian form when dealing with trigonometric functions.

Verification of the calculator's result by manually calculating the derivative.

Conclusion and invitation for viewers to subscribe, like, and comment with their questions.

Transcripts

Browse More Related Video

CASIO FX 991ES PLUS - Calculator skills - differentiation

Calculus - Finding the derivative at a point using a Ti-83 or 84 calcululator

Casio FX-991EX Differentiation Tutorial: How to Find Derivatives on Your Casio Calculator

Evaluating Functions - Basic Introduction | Algebra

Implicit Differentiation | Basic Calculus

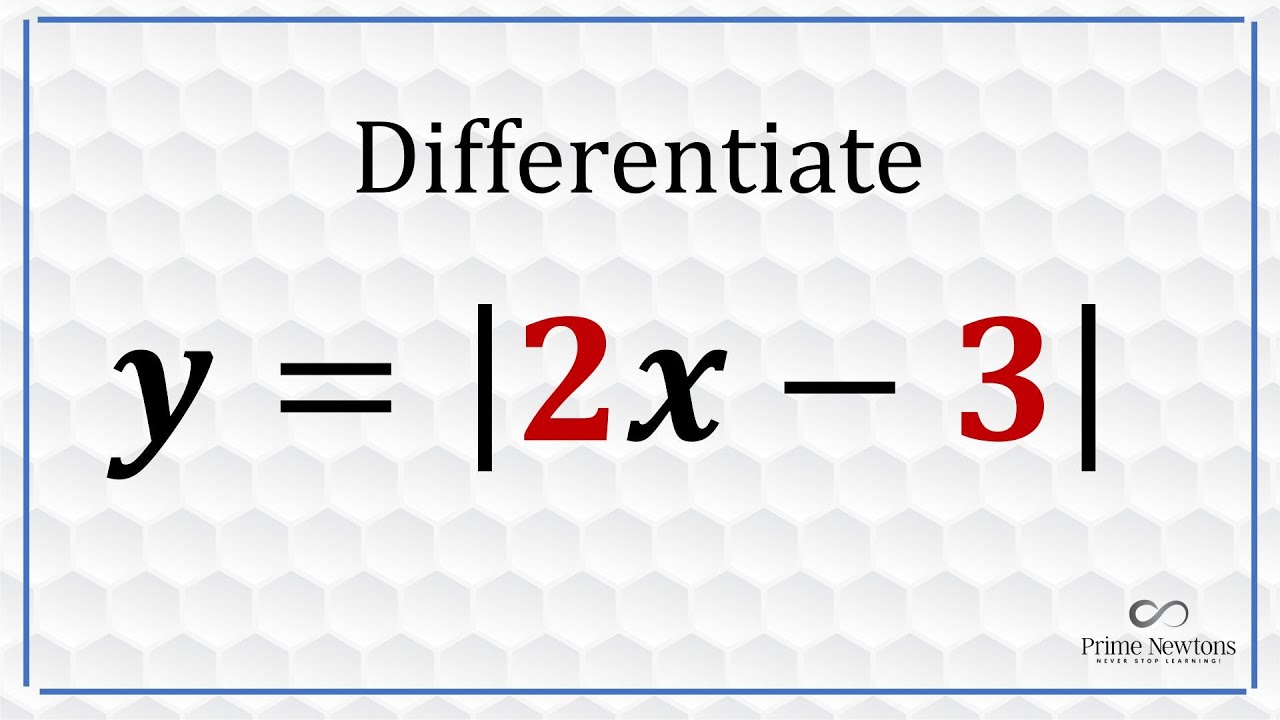
Derivative of absolute value function

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusDifferentiationEducationalMathematicsCalculatorTutorialVerificationDerivativeSolve ProblemsLearning