Casio FX-991EX Differentiation Tutorial: How to Find Derivatives on Your Casio Calculator
TLDRThis instructional video demonstrates how to utilize the differentiation functions of a Casio Classworks calculator to evaluate derivatives numerically. Although it doesn't perform symbolic differentiation, the calculator can find the derivative at a specific point and verify the correctness of manually calculated derivatives. The tutorial covers the process of evaluating the derivative of a function like x squared plus one at x equals one, yielding a result of two. Additionally, it shows how to use the calculator to confirm the accuracy of a derivative for a function such as y equals x cubed plus two x plus four, by comparing the calculator's numerical derivative to a suspected derivative. The video guides through entering functions into the calculator, using table mode for comparison, and ensuring that the values of f(x) and the suspected derivative g(x) match, thereby validating the correctness of the derivative.
Takeaways
- 📚 The video demonstrates how to use a Casio ClassWorks calculator for differentiation tasks.
- 🔍 The calculator does not perform symbolic differentiation; it evaluates derivatives numerically.
- 📈 It can find the derivative of a function at a specific point, which is useful for stationary point analysis.
- 📝 The calculator can also verify the correctness of a manually derived function's derivative.
- 👉 To find a derivative at a point, use the 'shift' function and input 'd/dx' followed by the function.
- 🔢 For example, to find the derivative of x^2 + 1 at x = 1, input the function and evaluate it to get the result.
- 📊 To check a derivative, define 'f(x)' as the original function and 'g(x)' as the suspected derivative.
- 📋 Input both 'f(x)' and 'g(x)' into the calculator and use table mode to compare the values at various points.
- 🔗 If 'f(x)' and 'g(x)' values match across a range, it confirms the correctness of the derivative.
- 👍 The video encourages viewers to like and subscribe for more helpful content.
- 🙏 The presenter expresses gratitude for watching and offers assistance in understanding differentiation with a calculator.
Q & A
What is the main purpose of the Casio Classworks calculator in the context of the video?
-The main purpose of the Casio Classworks calculator, as discussed in the video, is to evaluate the derivative of a function numerically and to check the correctness of a manually derived function.
Can the Casio Classworks calculator perform symbolic differentiation?
-No, the Casio Classworks calculator cannot perform symbolic differentiation. It is only capable of evaluating derivatives numerically.
How does the calculator find the derivative of a function at a specific point?
-To find the derivative at a specific point, you press shift and access 'd by dx', type in the function, and then evaluate it at the desired point by substituting the value of x.
What is an example function given in the video to demonstrate finding the derivative at a point?
-The example function given in the video is 'x squared plus 1', and it demonstrates evaluating the derivative at the point where x equals one.
What is the result of differentiating 'x squared plus 1' at x equals one?
-The result of differentiating 'x squared plus 1' at x equals one is two, as the derivative of the function is '2x' and substituting x with one gives 2.
How can the calculator be used to check if a derived function is correct?
-The calculator can be used to check the correctness of a derived function by defining 'f(x)' as the original function and 'g(x)' as the derived function, then comparing the values of 'f(x)' and 'g(x)' across a range of x values.
What is the process of checking the correctness of a derivative using the calculator?
-To check the correctness of a derivative, you define 'f(x)' with the original function, set 'g(x)' to what you believe the derivative is, input both into the calculator, go into table mode, and compare the values of 'f(x)' and 'g(x)' over a range of x values.
What does the video suggest if the values of 'f(x)' and 'g(x)' are not the same?
-If the values of 'f(x)' and 'g(x)' are not the same, it indicates that the manually derived function is incorrect and needs to be double-checked.
What does it mean if all values of 'f(x)' and 'g(x)' come out exactly the same in the calculator?
-If all values of 'f(x)' and 'g(x)' come out exactly the same, it proves that the manually derived function is correct.
What is the recommended range and step for checking the correctness of a derivative in the calculator?
-The video suggests using a wide range of x values, from negative five up to five, with a step of one for checking the correctness of a derivative.
Outlines
📚 Introduction to Numerical Differentiation on Casio ClassWiz Calculator
This paragraph introduces the video's purpose, which is to demonstrate how to use the differentiation functions on a Casio ClassWiz calculator. It clarifies that the calculator does not perform symbolic differentiation but can evaluate derivatives numerically. The video will cover two main applications: finding the derivative at a specific point and using the calculator to verify the correctness of a manually derived function. The example of finding the derivative of x squared plus 1 at x equals one is given, with a step-by-step guide on how to input and evaluate this on the calculator, resulting in the correct derivative value of two.
🔍 Verifying Derivatives Using the Calculator
The second part of the video focuses on using the calculator to check the accuracy of a derived function. It provides an example with the function y equals x cubed plus two x plus four, and the assumed correct derivative three x squared plus two. The process involves defining f(x) as the original function and g(x) as the assumed derivative, then comparing these at various points by entering them into the calculator's table mode. The table mode is accessed through the menu, and the function and its derivative are inputted for evaluation across a range of x values. If the values of f(x) and g(x) match across the range, it confirms that the derivative is correct, serving as a useful tool for verifying derivatives during exam preparation or study.
Mindmap
Keywords
💡Differentiation
💡Casio ClassWorks Calculator
💡Symbolic Differentiation
💡Numerical Differentiation
💡Derivative at a Given Point
💡Checking Derivatives
💡Stationary Points
💡Function Definition
💡Table Mode
💡Range and Step
Highlights
The video demonstrates how to use the differentiation functions on a Casio Classworks calculator.
The calculator cannot perform symbolic differentiation, so it can't provide the derivative of a function directly.
It can evaluate the derivative numerically.
The calculator can find the derivative at a given point.
It is useful for checking the correctness of a derivative.
Example given: finding the derivative of x squared plus 1 at x equals one.
The process involves pressing shift and accessing d by dx.
The calculator evaluates the derivative at a specific point and gives the value.
The derivative of x squared plus 1 at x=1 is correctly evaluated as 2.
The calculator can be used to investigate stationary points.
It can help prove the correctness of a manually derived function.
An example function y = x cubed plus two x plus four is given for demonstration.
The correct derivative of the example function is three x squared plus two.
The process of proving the derivative involves defining f(x) and g(x) on the calculator.
Entering the function and its derivative into the calculator's table mode for comparison.
If f(x) and g(x) values match, it proves the derivative is correct.
The calculator can be used as a tool to check and confirm the accuracy of derivatives.
A call to action for viewers to like and subscribe if the video was helpful.
Transcripts
Browse More Related Video

TI-84 Calculator - 10 - Calculating Derivatives and Integrals

differentiation in calculator fx-991MS #differentiation

Inflection points (algebraic) | AP Calculus AB | Khan Academy
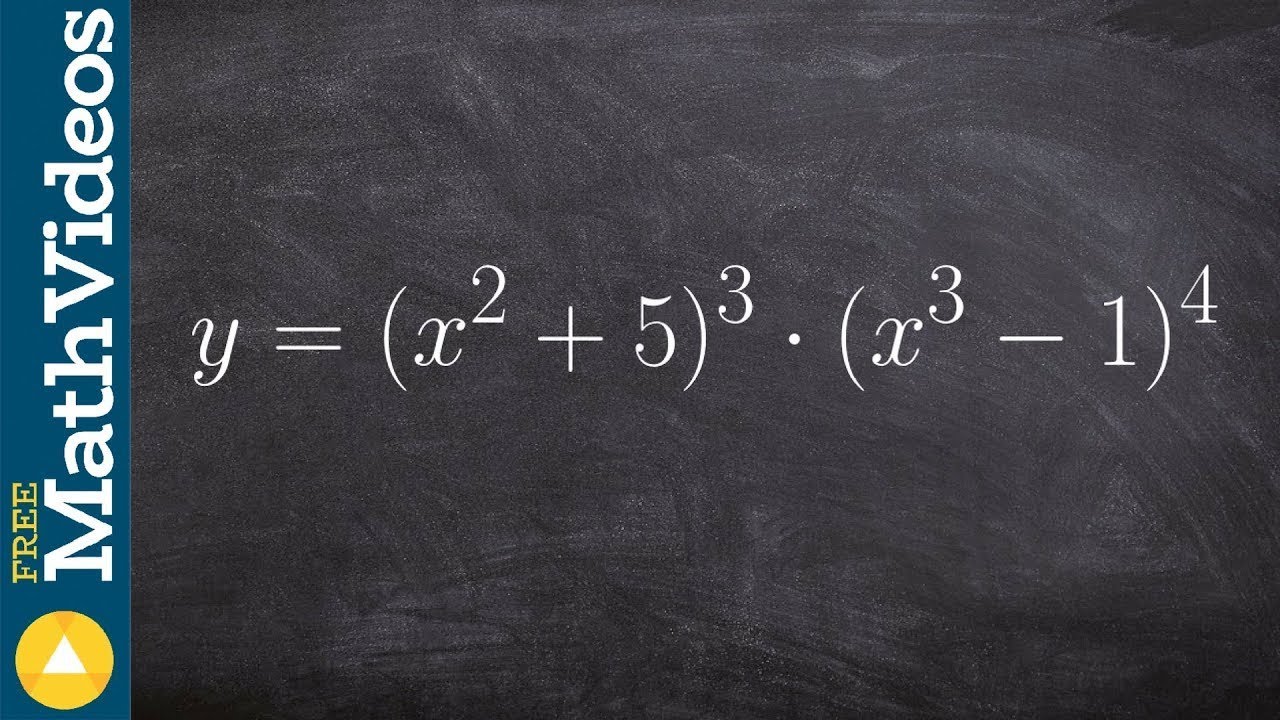
Taking the derivative of two binomials using product and chain rule

CASIO FX 991ES PLUS - Calculator skills - differentiation
Lesson 3 1B Using the Calculator to find Derivatives and Critical Numbers
5.0 / 5 (0 votes)
Thanks for rating: