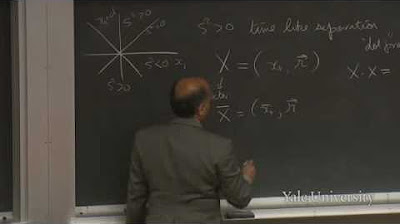15. Four-Vector in Relativity
TLDRThe transcript is a detailed lecture on the concepts of space-time and relativistic dynamics. The lecturer begins by discussing the four-dimensional nature of space-time, represented by coordinates (ct, x, y, z), and introduces the Lorentz transformation for transitioning between different frames of reference. The importance of the space-time interval, invariant under Lorentz transformations, is emphasized. The lecture then delves into the construction of the four-momentum vector, which combines energy and momentum, and its significance in special relativity. The components of the four-momentum vector are derived, highlighting the relationship between energy, momentum, and mass. The lecturer also addresses the unique case of photons, which have energy and momentum but no rest mass, leading to different conservation laws. The discussion concludes with an application of these concepts to collision problems, showcasing how to calculate the minimum energy required to produce proton/anti-proton pairs in a collider, and the strategic use of the center of mass frame for such calculations.
Takeaways
- 📐 **Four-Dimensional Space-Time**: Space-time is described by four coordinates (x_0, x_1, x_2, x_3), often simplified to include only the x direction when y and z remain constant during frame transitions.
- 🧵 **Vector Representation**: The four coordinates are combined into a single vector **r**, emphasizing the four-dimensional nature of space-time.
- 🎭 **Lorentz Transformation**: The transformation between different frames of reference is given by specific formulas involving **β** (the velocity v divided by the speed of light c) and **γ** (the Lorentz factor).
- ⚙️ **Space-Time Interval**: The interval **s^(2)** is invariant under Lorentz transformations, analogous to the constancy of the distance from the origin in a rotated frame.
- 🚀 **Momentum Vector in Relativity**: The momentum vector in relativistic theory is not just mass times velocity but includes additional factors to account for time dilation and length contraction.
- 🌟 **Energy-Momentum Four-Vector**: The energy-momentum four-vector combines energy and momentum into a single object that transforms under Lorentz transformations, with **p_0** representing energy divided by c.
- 🤝 **Conservation Laws**: In relativistic collisions, energy and momentum are conserved, and these conservation laws apply across all frames of reference due to the four-vector nature of energy and momentum.
- 🔄 **Invariance of Four-Vector Dot Product**: The dot product of any four-vector with itself is invariant, meaning it has the same value for all observers, which is crucial for defining quantities like rest mass and energy.
- 💡 **Practical Understanding**: For practical purposes, one should understand the operational definitions of relativistic momentum and energy, as well as how they combine to form the energy-momentum four-vector.
- 📌 **Significance of the Four-Vector**: The importance of the energy and momentum forming a four-vector lies in ensuring that conservation laws hold in all frames of reference, not just in a single observer's frame.
- ⚛️ **Photons in Relativity**: Photons, particles with no rest mass, have energy and momentum that obey the equation E^2 = (c * p)^2, with the energy being equal to the product of momentum and the speed of light.
Q & A
What is the significance of the four coordinates (c, t, x, y, z) in describing space-time?
-The four coordinates (c, t, x, y, z) are used to describe space-time in the context of special relativity. They allow for the labeling of an event or particle with four numbers, which can be combined into a single vector r. These coordinates are essential for understanding how space and time are interconnected and how they transform under different frames of reference.
What does the notation x_0, x_1, x_2, x_3 represent in the context of the transcript?
-The notation x_0, x_1, x_2, x_3 represents the four components of the space-time vector r. Here, x_1 typically represents the x-coordinate, x_2 represents the y-coordinate, x_3 represents the z-coordinate, and x_0 is often used to denote the time coordinate ct, where c is the speed of light.
Why is the term β (beta) introduced in the context of the Lorentz transformation?
-The term β (beta) is introduced as the ratio of the relative velocity (v) of a frame to the speed of light (c), i.e., β = v/c. It is used in the Lorentz transformation equations to describe how space and time coordinates transform when switching between two frames of reference that are moving relative to each other.
What is the role of the Lorentz transformation in special relativity?
-The Lorentz transformation is crucial in special relativity as it provides the mathematical relationship between the space and time coordinates of an event as observed in two different inertial frames of reference. It ensures that the laws of physics remain the same in all inertial frames, which is a fundamental postulate of special relativity.
What is the space-time interval Δs^(2), and why is it considered invariant?
-The space-time interval Δs^(2) is a quantity that represents the 'distance' between two events in space-time, defined as the square of the time-like part minus the square of the space-like part of the space-time separation. It is invariant under Lorentz transformations, meaning it has the same value for all observers, regardless of their relative motion. This invariance is a key feature of the space-time structure in special relativity.
How is the four-momentum p defined in the context of special relativity?
-In special relativity, the four-momentum p is defined as a four-vector that combines the energy and momentum of a particle. It is given by p = (E/c, p_x, p_y, p_z), where E is the energy of the particle, and p_x, p_y, p_z are its spatial momentum components. The four-momentum transforms under Lorentz transformations in a way that maintains the invariance of the space-time interval.
What is the relationship between the energy E and momentum p of a particle as described in the transcript?
-The relationship between the energy E and momentum p of a particle is given by the equation E^(2) = (c * p)^(2) + (m*c^2)^2, which can be rearranged to E = sqrt((c * p)^(2) + (m*c^2)^2). This equation shows that the energy of a particle is not simply its rest mass energy (m*c^2), but also includes the kinetic energy associated with its momentum.
How does the concept of proper time τ relate to the momentum of a particle?
-The concept of proper time τ is used to define the momentum of a particle in a way that is invariant across different frames of reference. The momentum four-vector is defined in terms of the change in the four-position divided by dτ, where dτ is the time elapsed according to the particle itself. This ensures that the definition of momentum is consistent regardless of the observer's frame of reference.
What is the significance of the equation E^2 = c^2p^2 + m^2c^4 in the context of the energy-momentum relationship?
-The equation E^2 = c^2p^2 + m^2c^4 is a relativistic energy-momentum relation that shows the total energy E of a particle is the sum of its rest energy (m*c^2) and its kinetic energy (c^2 times the magnitude of its momentum p). This equation is fundamental to understanding the interplay between energy and momentum in special relativity and is invariant under Lorentz transformations.
How is the rest mass m of a particle related to its energy and momentum in the context of special relativity?
-In special relativity, the rest mass m of a particle is related to its energy and momentum through the invariant equation E^2 = (c * p)^2 + (m*c^2)^2. This equation implies that the mass of a particle, as observed in any frame, is a measure of its energy content, with the rest mass energy being a part of its total energy.
What is the condition for a photon's four-momentum, and how does it differ from that of a massive particle?
-For a photon, which has no rest mass, the condition for its four-momentum is that the square of the four-momentum (K dot K) is zero. This is different from a massive particle, for which the square of the four-momentum is equal to m^2c^2, indicating that the photon's energy and momentum are related by E = pc, with no rest mass term present.
Outlines
📚 Introduction to Space-Time and Four-Dimensional Coordinates
The paragraph begins by recapping the complexity of the last class, emphasizing the four coordinates that describe space-time: x_0 (ct), x_1 (x), x_2 (y), and x_3 (z), combined into a single vector r. The professor discusses the choice to sometimes omit y and z when motion is only in the x direction. The concept of a moving frame is introduced with the transformation equations x'_1 = x_1 - βx_0 and x'_0 = x_0 - βx_1, where β is v/c, and γ is used to simplify the equations. The importance of the space-time interval, denoted as Δs^2, is highlighted as an invariant quantity under Lorentz transformations.
🚀 Derivation of Momentum Vector in Relativistic Context
The paragraph delves into the classical definition of momentum and how it is derived from the change in position over time. The professor then transitions to defining the momentum in the context of special relativity, emphasizing the need to divide by a quantity that is the same for all observers. The concept of proper time τ is introduced as the time elapsed according to the particle itself, which leads to the definition of four-momentum p as m(dx_0/dτ, dx_1/dτ). The components of this four-momentum are discussed, and the student-teacher interaction clarifies the inclusion of c in the momentum components.
🧲 Defining Four-Momentum and its Components
The paragraph explains the construction of the four-momentum vector, which consists of a time component and a spatial component. The time component is the energy divided by c, and the spatial component is the momentum. The professor shows how the four-momentum transforms under Lorentz transformations, similar to the space-time coordinates. The emphasis is on understanding the operational significance of the four-momentum vector in terms of the observer's frame of reference.
🌟 Energy-Momentum Relation and its Significance
The paragraph explores the relationship between energy and momentum, leading to the realization that the zero component of the four-momentum is the energy of the particle divided by c. The professor discusses the expansion of this relationship at low velocities and how it relates to the rest mass and kinetic energy of the particle. The energy-momentum four-vector is defined, and its invariance under Lorentz transformations is highlighted. The paragraph concludes with a discussion on the operational knowledge required for understanding particle dynamics in relativity.
💫 Relativistic Momentum and Energy for Particles and Photons
The paragraph discusses the relativistic momentum and energy for particles with mass and for massless particles like photons. It emphasizes that while particles with mass follow a modified momentum equation, photons have a unique relationship where their energy is equal to their momentum times the speed of light (E = pc). The concept of the four-momentum vector's invariant length square is introduced, and it's shown that for any particle, this length is m^(2)c^(2), which is independent of the particle's velocity.
🚨 Conservation Laws and Four-Vector Properties in Collisions
The paragraph focuses on the conservation of energy and momentum in the context of collisions. It is explained that these quantities, now combined into a four-vector, must be conserved in all frames of reference. The professor illustrates why the conservation laws hold true for all observers by using the properties of four-vectors and their transformation under Lorentz transformations. The importance of using the correct relativistic definition of momentum is emphasized to ensure that conservation laws are universally applicable.
🧙♂️ The Role of Mass in Relativistic Collisions
The paragraph discusses the concept of mass in relativistic collisions. It is clarified that the only universally agreed upon mass is the rest mass, which is the same for all observers regardless of the particle's state of motion. The professor also addresses the process of balancing energy and momentum in a collision using the four-momentum vector before and after the collision. The emphasis is on the practical application of these concepts in solving problems involving relativistic kinematics.
🔋 Minimum Energy Requirement for Particle Production
The paragraph explores the minimum energy required to produce particles in a collider, using the example of a proton-proton collision producing proton-antiproton pairs. The professor explains the importance of considering the center of mass frame, where the total momentum is zero, allowing for the simplest scenario of particle production. The calculation leads to the conclusion that the incoming proton must have an energy of 7 times its rest mass-energy to facilitate the production of the particle-antiparticle pair, highlighting the conversion of energy into mass in particle accelerators.
Mindmap
Keywords
💡Space-time
💡Lorentz transformation
💡Four-vector
💡Momentum
💡Energy-momentum four-vector
💡Invariant
💡Time dilation
💡Mass-energy equivalence
💡Photon
💡Relativistic collision
💡Center of mass frame
Highlights
Space-time is described by four coordinates, forming a single vector r, which includes time and position.
The concept of four-dimensional space-time includes a mix of space and time when switching frames of reference.
Introduces the Lorentz transformation and its relation to the velocity of a particle and the speed of light.
Defines the space-time interval Δs^2, which is invariant under Lorentz transformations, analogous to the length of a vector.
Explains the construction of the momentum vector in classical physics and its extension to special relativity.
Derives the four-momentum vector p, which includes energy and momentum components.
Discusses the relationship between the time elapsed according to an observer and the time elapsed according to a moving particle.
Relates the energy-momentum four-vector to the conservation laws in particle collisions.
Details how the four-momentum transforms under Lorentz transformations, similar to space-time coordinates.
Explains that the invariant length square of the momentum four-vector is m^2c^2, which is independent of the particle's velocity.
Describes the special case of photons, which have energy and momentum but no rest mass, and obey E = pc.
Illustrates the use of four-vectors in calculating relativistic collisions, emphasizing that conservation laws must hold for all observers.
Provides a shortcut for calculating the dot product of four-vectors by using the center of mass frame.
Demonstrates how to calculate the minimum energy required to produce proton/anti-proton pairs in a collider.
Advises on the use of c=1 in calculations for simplicity, reminding that factors of c can be reintroduced later.
Stresses the importance of understanding the conservation of four-momentum in all frames of reference for collision problems.
Encourages students to practice relativistic kinematics problems to gain proficiency in the subject.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: