Extreme value theorem | Existence theorems | AP Calculus AB | Khan Academy
TLDRThe video script discusses the Extreme Value Theorem, which states that a continuous function over a closed interval from a to b will have an absolute maximum and minimum value. The script emphasizes the importance of continuity and the inclusion of endpoints in the interval. It illustrates the theorem with examples and contrasts it with non-continuous functions and open intervals, showing why these conditions are necessary. The presenter also challenges viewers to think about edge cases and construct a non-continuous function over a closed interval to deepen their understanding of why the theorem is stated as it is.
Takeaways
- 📚 The Extreme Value Theorem states that if a function is continuous over a closed interval [a, b], it has both an absolute maximum and minimum value on that interval.
- 🔍 The theorem is intuitive but important to understand why it requires continuity and a closed interval for its validity.
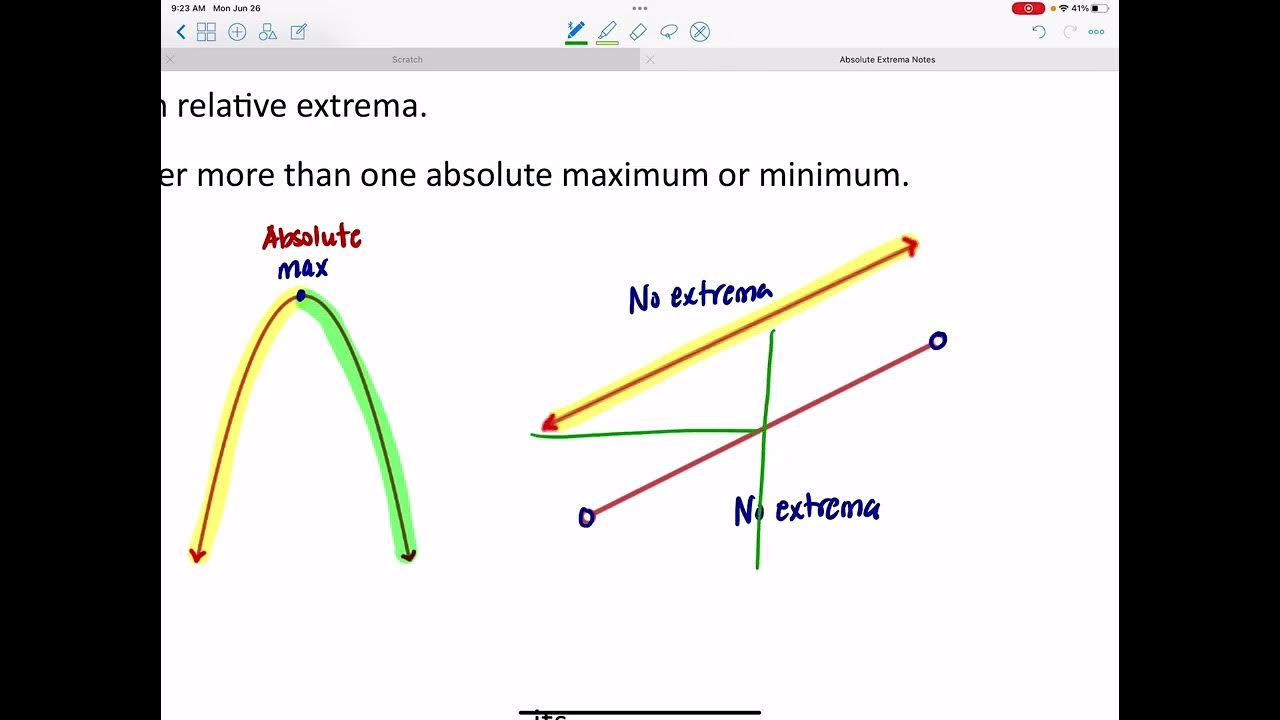
- 📈 The script illustrates the concept by drawing a continuous function over an interval, showing that it's clear where the maximum and minimum points are.
- 🤔 The script invites the viewer to consider why continuity is necessary, hinting that without it, it's difficult to define maximum or minimum values.
- 📉 The importance of a closed interval is highlighted by discussing the difficulty in identifying extreme values on an open interval where endpoints are not included.
- 📌 The script uses logical notation to express that there exist points c and d within the interval where f(c) is the minimum and f(d) is the maximum.
- 📐 It's explained that for any x in the interval, f(x) will be between f(c) and f(d), reinforcing the idea that c and d are the absolute minimum and maximum points, respectively.
- 💡 The script suggests that while the theorem seems obvious, understanding the conditions (continuity and closed interval) is crucial for its application.
- 🚫 The script points out that without continuity, a function might not have a well-defined maximum or minimum, as it could approach but never reach certain values.
- 🔑 The inclusion of endpoints a and b in the interval is essential because they could be the actual maximum or minimum values, which would be missed if the interval were open.
- 📝 The script encourages viewers to pause and consider constructing a non-continuous function over a closed interval to better understand the theorem's conditions.
Q & A
What is the Extreme Value Theorem?
-The Extreme Value Theorem states that if a function is continuous over a closed interval from a to b, including the endpoints, then there exists an absolute maximum and an absolute minimum value for the function over that interval.
Why is it necessary for the function to be continuous in the Extreme Value Theorem?
-Continuity is necessary because without it, a function might not have a well-defined maximum or minimum over an interval. A non-continuous function could have points where it is undefined, making it impossible to determine the extreme values.
What does a closed interval mean in the context of the Extreme Value Theorem?
-A closed interval includes both the endpoints, a and b, which means that the function is defined and continuous at these points as well as between them.
Why do we need to include the endpoints in the closed interval when considering extreme values?
-Including the endpoints is important because the maximum or minimum value could occur exactly at these points. If the interval were open, we might miss the actual maximum or minimum values that occur at the endpoints.
Can the extreme values of a continuous function over a closed interval occur at the endpoints?
-Yes, the extreme values can occur at the endpoints. The theorem ensures that the endpoints are considered as potential locations for the maximum and minimum values.
What happens if we consider an open interval instead of a closed one?
-In an open interval, the endpoints are not included. This means that even if the function approaches a maximum or minimum value as it gets arbitrarily close to an endpoint, that value cannot be considered the extreme value because the function is not defined at that exact point.
Can a function have multiple maximum or minimum points over an interval?
-No, according to the Extreme Value Theorem, there is exactly one absolute maximum and one absolute minimum value for a continuous function over a closed interval.
Is it possible for a function to have the same value at multiple points over an interval?
-Yes, a function can have the same value at multiple points, but the Extreme Value Theorem refers to the absolute maximum and minimum values, which are unique.
How can you determine the extreme values of a function without calculus?
-One can determine the extreme values by evaluating the function at the critical points (where the derivative is zero or undefined) and at the endpoints of the interval, and then comparing these values.
What is an example of a function that is not continuous over an interval?
-An example of a non-continuous function could be a step function or a function with a vertical asymptote, where the function is not defined at certain points within the interval.
Why is it important to understand the conditions under which the Extreme Value Theorem applies?
-Understanding the conditions ensures that you can correctly apply the theorem to find the extreme values of a function. It also helps in identifying when alternative methods or theorems might be needed for functions that do not meet these conditions.
Outlines
📚 Introduction to the Extreme Value Theorem
This paragraph introduces the Extreme Value Theorem, which is a fundamental concept in calculus. It explains that for any continuous function over a closed interval, including the endpoints, there must exist an absolute maximum and minimum value. The paragraph uses a visual representation to illustrate this point, drawing a continuous function over an interval from 'a' to 'b'. It highlights the intuitive nature of the theorem, prompting the viewer to consider why the theorem requires continuity and why it must be applied to a closed interval. The explanation includes the logical notation for 'there exists' and describes how to identify the points 'c' and 'd' where the minimum and maximum values occur, respectively.
🔍 Importance of Continuity and Closed Intervals
The second paragraph delves deeper into the necessity of continuity and the closed nature of the interval in the Extreme Value Theorem. It challenges the viewer to think of a non-continuous function where it's difficult to define a maximum or minimum value over a closed interval. The speaker then provides an example of such a function, where the function is undefined at points where one might expect a maximum or minimum. This illustrates the importance of continuity for the theorem to hold true. Additionally, the paragraph discusses why endpoints must be included in the interval, using the concept of an open interval as a contrasting example. It shows that without the endpoints, one could approach but never reach a maximum or minimum value, thus emphasizing the significance of the closed interval in the theorem.
Mindmap
Keywords
💡Extreme Value Theorem
💡Closed Interval
💡Continuity
💡Absolute Maximum and Minimum
💡Logical Notation
💡Endpoints
💡Open Interval
💡Graph
💡Flat Function
💡Non-Continuous Function
Highlights
The extreme value theorem states that a continuous function over a closed interval will have an absolute maximum and minimum value.
A closed interval includes the endpoints, denoted by brackets [a, b].
The theorem seems intuitive, but the conditions of continuity and a closed interval are crucial.
A continuous function can be visualized without lifting the pen while drawing its graph.
The absolute maximum and minimum points can be identified on the graph of a continuous function.
The logical notation for 'there exists' is used to express the existence of maximum and minimum values.
For a continuous function, there exist points c and d in the interval where f(c) ≤ f(x) ≤ f(d) for all x in the interval.
Different continuous functions can have their maximum and minimum points at various locations within the interval.
A flat function can have any point as a maximum or minimum.
The necessity of continuity is demonstrated by constructing a non-continuous function with no clear maximum or minimum.
A non-continuous function can approach but never reach a limit, thus lacking a maximum or minimum.
The importance of a closed interval is that endpoints are considered as potential maximum and minimum points.
An open interval does not include endpoints, which can lead to missing the actual maximum or minimum values.
The theorem's intuitive nature is contrasted with the importance of its specific conditions.
Understanding why the theorem is stated as it is helps in appreciating the role of continuity and closed intervals.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: