Car on a banked curve

Physics with Professor Matt Anderson

10 Apr 201616:02

EducationalLearning

32 Likes 10 Comments

TLDRThis script delves into the physics of a banked curve, a common feature in road design to allow vehicles to navigate turns without relying on friction. It guides through a step-by-step analysis, starting with a free body diagram of forces acting on a car, then applying Newton's second law to derive the relationship between speed, radius, and the banking angle. The presenter illustrates the concept with an example of a freeway off-ramp, calculating the necessary bank angle to safely navigate at the posted speed without skidding, especially in icy conditions. The script concludes with an intriguing experiment to experience the natural steering effect of a correctly banked curve.

Takeaways

😀 The script starts with a casual greeting and an invitation for the audience to interact with the host.
🔍 The main topic discussed is solving a banked curve problem in physics, involving kinematics and forces acting on a car.
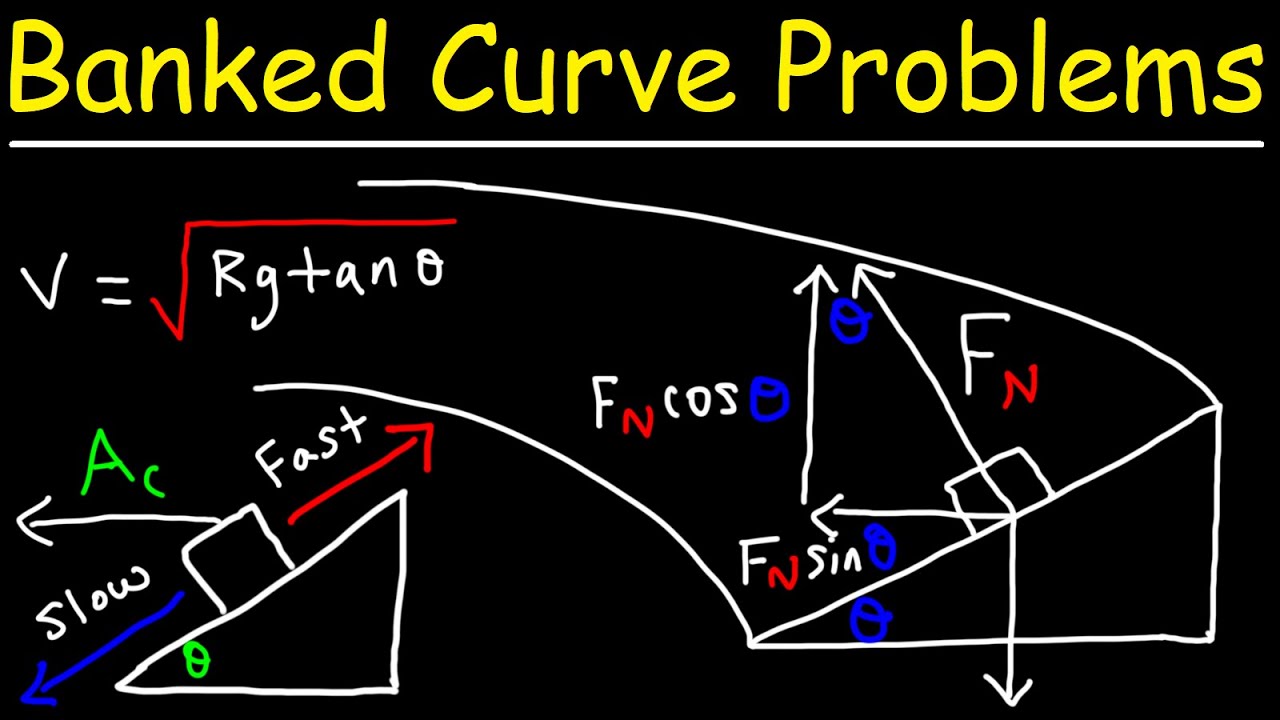
🚗 The script describes a car on a banked curve, emphasizing the importance of understanding the relationship between velocity (V), angle (theta), and radius (R).
📐 A free body diagram is introduced to visualize the forces acting on the car, including gravity and the normal force, with a focus on orthogonal components.
🧩 The script walks through a thought experiment of driving on ice to eliminate friction and simplify the force analysis.
📉 The importance of correctly breaking down the normal force into its components is highlighted, using trigonometric relationships with the angle theta.
🔧 Newton's second law is applied to the radial direction to find the relationship between the normal force and the centripetal force required for circular motion.
📚 The script provides a step-by-step approach to solving for the angle of the banked curve using the equations derived from Newton's laws.
🔢 A practical example is given with hypothetical numbers to demonstrate how to calculate the angle of a banked curve, such as a freeway off-ramp.
🛣️ The significance of the calculated angle is explained in the context of road design, especially for safety in conditions with reduced friction like snow or ice.
🚨 The script concludes with a call to action for the audience to experience the effect of a properly banked curve by driving at the posted speed limit on a freeway off-ramp.

Q & A

What is the main topic discussed in the video script?
-The main topic discussed in the video script is the physics of a banked curve, specifically how to calculate the angle of banking required for a vehicle to navigate a curve without relying on friction.
What is the purpose of a banked curve in road design?
-The purpose of a banked curve in road design is to allow vehicles to navigate turns at higher speeds without the need for friction between the tires and the road, which is particularly useful in conditions like snow or ice.
What forces are considered when analyzing a car on a banked curve?
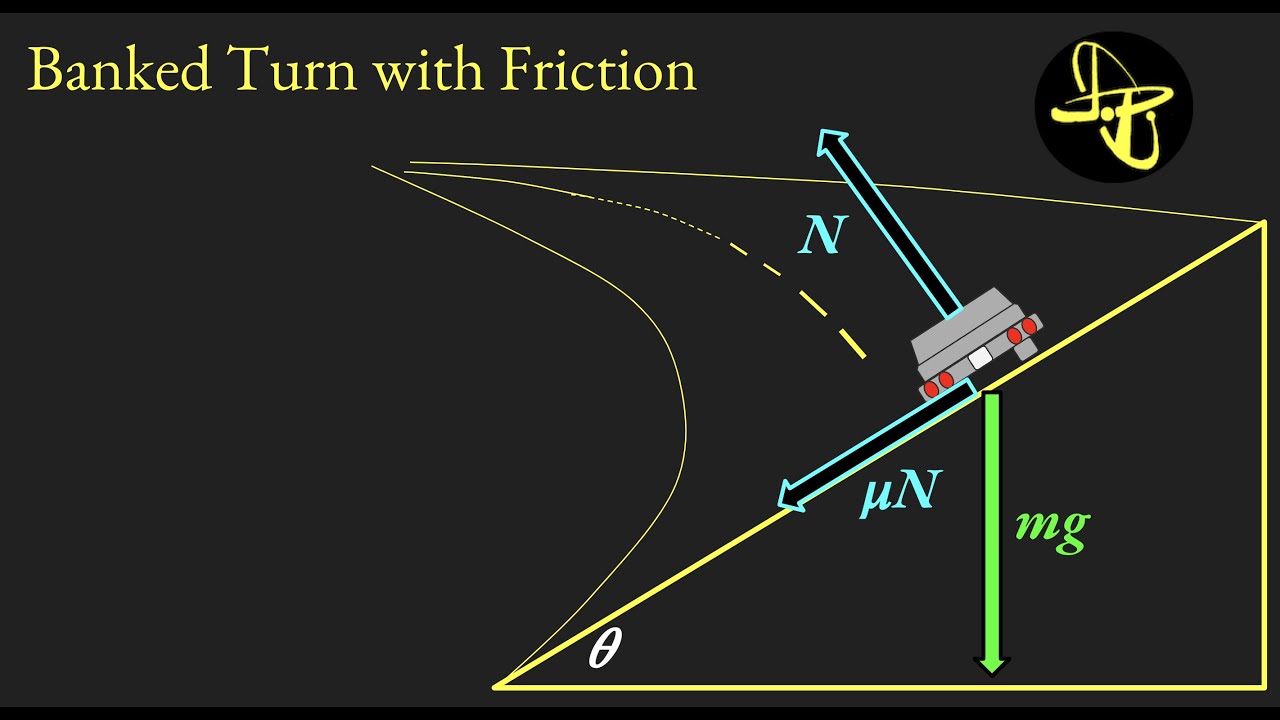
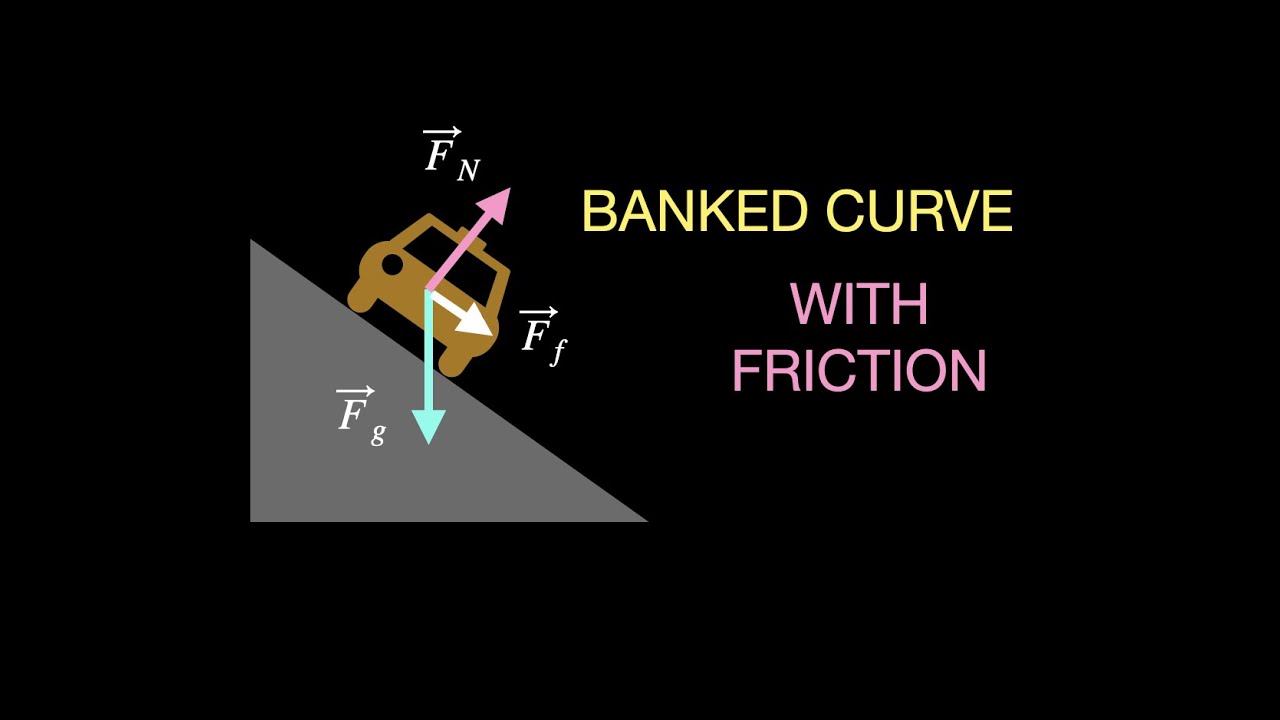
-When analyzing a car on a banked curve, the forces considered are gravity (mg), the normal force, and static friction (though in the ice scenario, friction is neglected).
Why is it important to have orthogonal forces in the free body diagram?
-Orthogonal forces are important in the free body diagram because they simplify the application of Newton's laws, allowing for easier calculation of the components of forces in the x and y directions.
How does the script suggest determining the correct components of the normal force?
-The script suggests using the limits of the angle theta to determine the correct components of the normal force. By setting theta to 0 degrees and understanding the forces acting on the car, one can deduce the correct components.
What is the formula derived from Newton's second law for circular motion in the radial direction?
-The formula derived from Newton's second law for circular motion in the radial direction is n * sine(theta) = MV^2 / R, where n is the normal force, theta is the angle of the bank, V is the velocity, and R is the radius of curvature.
How can the angle of the bank (theta) be calculated?
-The angle of the bank (theta) can be calculated using the formula V^2 / (g * R), where V is the velocity, g is the acceleration due to gravity, and R is the radius of curvature. The arctangent of this ratio gives the required angle theta.
What is a typical speed for a freeway off-ramp, according to the script?
-According to the script, a typical speed for a freeway off-ramp is 45 miles per hour, which is approximately 20 meters per second.
Why is the calculation of the bank angle important for engineers?
-The calculation of the bank angle is important for engineers because it ensures that road designs can accommodate vehicles safely navigating curves at the posted speed, even under adverse conditions like snow or ice.
What is the experiment suggested in the script to understand the effect of banked curves?
-The experiment suggested in the script is to drive on a freeway off-ramp at the posted speed limit to experience how the car naturally navigates the curve without the need for significant steering input.

Outlines

00:00

🚗 Introduction to Banked Curve Kinematics

The script begins with a friendly greeting and an invitation for viewers to engage in a conversation about a banked curve problem. It sets the scene with a visual of a car on a banked curve, aiming to explore the relationship between velocity (V), angle of bank (theta), and radius (R) of the curve. The speaker introduces a Free Body Diagram to analyze the forces acting on the car, such as gravity and the normal force, and discusses the hypothetical scenario of driving on ice to eliminate friction, simplifying the forces to just the normal force and gravity. The goal is to understand how these forces can be resolved into components to solve the problem.

05:00

📐 Resolving Forces and Applying Newton's Second Law

This paragraph delves into the process of resolving the forces acting on the car into orthogonal components, using trigonometric relationships with the angle of bank (theta). The speaker corrects an initial mistake in the force components, leading to the correct Free Body Diagram with gravity acting downward and the normal force resolved into horizontal and vertical components. Newton's second law is then applied to the radial direction, resulting in an equation relating the normal force, velocity, and radius. Another equation is derived from the vertical forces balance, leading to a relationship between the normal force and gravitational force. The speaker then cleverly combines these equations to eliminate variables and derive a formula for the angle of bank in terms of known quantities.

10:05

🔢 Calculating the Angle of Bank for a Freeway Off-Ramp

The script continues with a practical example, estimating the angle of bank needed for a freeway off-ramp where the typical speed is 45 miles per hour, converted to 20 meters per second. The speaker guesses the radius of curvature to be around 50 meters based on everyday experience and uses the derived formula to calculate the angle of bank. The calculation involves taking the arctangent of the ratio of the squared velocity to the product of gravitational acceleration and radius, resulting in an angle of approximately 39 degrees. This angle represents the steepness required for the bank to allow vehicles to navigate the curve without relying on friction, which is crucial during icy or snowy conditions.

15:07

🚦 The Importance of Banked Curves in Road Design

In the final paragraph, the speaker emphasizes the importance of understanding banked curves for engineers, especially in road design. They explain that the calculated angle of bank ensures that drivers can safely navigate curves even without friction, such as on black ice. The speaker also shares a personal anecdote about the dangers of black ice and encourages viewers to experiment with driving at the posted speed on a banked curve to experience how the car naturally follows the curve. The paragraph concludes with a humorous note, suggesting that viewers ignore the honking of other drivers while conducting this experiment.

Mindmap

Keywords

💡Kinematics

Kinematics is the branch of classical mechanics that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that caused the motion. In the video, kinematics is central to understanding how a car moves around a banked curve, analyzing the forces acting on the car and the relationship between velocity, radius, and angle of the curve.

💡Freebody Diagram

A freebody diagram is a simplified illustration that shows all the forces acting on an object in a particular situation, isolated from the rest of the system. In the script, the freebody diagram is used to visualize the forces on the car, such as gravity and normal force, and to understand how these forces decompose into components that affect the car's motion on a banked curve.

💡Normal Force

Normal force is the perpendicular force exerted by a surface that supports the weight of an object resting on it. In the context of the video, the normal force is critical in the analysis of a banked curve because it supports the car's weight and provides a component of force that helps the car navigate the curve without slipping.

💡Static Friction

Static friction is the force that prevents an object at rest from starting to move when a force is applied to it. In the video, the absence of static friction is considered in an experiment to simplify the analysis of forces acting on a car on a banked curve, emphasizing that the normal force alone can provide the necessary centripetal force for circular motion.

💡Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. The script uses trigonometry to decompose the normal force into components (sine and cosine) that are essential for solving the banked curve problem and determining the angle of the bank needed for safe vehicle motion.

💡Newton's Second Law

Newton's second law of motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. In the video, this law is applied to the radial direction of the car's motion on a banked curve, equating the net force (normal force component) to the centripetal force required for circular motion.

💡Centripetal Force

Centripetal force is the inward force that keeps an object moving in a circular path. The video discusses how the component of the normal force provides the centripetal force necessary for a car to turn on a banked curve, especially in the absence of friction.

💡Tangent

In trigonometry, the tangent of an angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side. The script uses the tangent function to relate the velocity, gravitational force, and radius of the curve, ultimately helping to solve for the angle of the banked curve.

💡Arc Tangent

The arc tangent, or inverse tangent, is used to find the angle whose tangent is a given number. In the script, the arc tangent is used to calculate the angle of the banked curve (theta) based on the known values of velocity, gravitational acceleration, and radius of curvature.

💡Banked Curve

A banked curve is a curve in a road or track that is elevated on one side to provide additional centripetal force, allowing vehicles to navigate the curve at higher speeds without relying on friction. The video's main theme revolves around understanding the physics of banked curves and how they are designed to improve safety and efficiency in vehicle motion.

💡Freeway Off-Ramp

A freeway off-ramp is a part of a highway system that allows vehicles to exit the freeway smoothly. The script uses the example of a freeway off-ramp to illustrate the practical application of the physics discussed, highlighting how the angle of banking is calculated to ensure safe and friction-independent turns.

Highlights

Introduction of the concept of banked curves and their importance in vehicle dynamics.

Explanation of the forces acting on a car in a banked curve: gravity and normal force.

The role of static friction in banked curves and its absence in an idealized scenario.

The significance of orthogonal forces in the free body diagram for banked curves.

Determining the correct components of normal force using the limit of theta approaching zero degrees.

The correct free body diagram with gravity and normal force components aligned with sine and cosine of theta.

Application of Newton's second law to the radial direction in circular motion.

Equation derivation for the force in the radial direction as n sine theta equals MV squared over R.

Analysis of vertical forces and the equation n cosine theta equals mg for no vertical acceleration.

Solving for the angle theta using the relationship between the two derived equations.

The practical application of banked curve calculations in designing freeway off-ramps.

The importance of banked curves in preventing vehicles from sliding off roads in icy conditions.

Anecdote about the experience of driving on black ice and the near absence of friction.

The recommendation for engineers to perform calculations to ensure safe bank angles for roads.

The experiment of driving at the posted speed on a freeway off-ramp to experience the natural turn.

The observation that drivers rarely adhere to the posted speed limits on off-ramps.

Encouragement for the audience to conduct the experiment and observe the car's steering behavior.

Transcripts

Browse More Related Video

Banked Turn with Friction - Physics of Speed Limits on Banked Curves

Banked turn Physics Problems

Banked Curve Physics - Uniform Circular Motion

Banked Curve with Friction: Finding Maximum and Minimum Speed

banked curves and circular motion explained

Maximum Speed Around a Banked Curve WITH Friction