Introduction to Simple Harmonic Motion (SHM) | General Equation and Derivation
TLDRThis script delves into the concept of simple harmonic motion, a type of periodic motion where the restoring force is directly proportional to the displacement from equilibrium. It uses a simple pendulum as an illustrative example and explores the mathematical foundations, introducing the proportionality constant 'k' and the angular frequency 'ω'. The script explains how the motion is described by differential equations and derives the equations for position and velocity, ultimately leading to the sinusoidal position function x = A sin(ωt + φ), where A is the amplitude, ω the angular frequency, t the time, and φ the phase constant, highlighting the phase constant's role in defining the initial displacement.
Takeaways
- 📚 Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force is directly proportional to the displacement from the equilibrium position.
- 🌀 The displacement in SHM is towards the equilibrium position, indicating that the restoring force acts in the opposite direction to the displacement.
- 🔍 A classic example of SHM is a simple pendulum, where the bob experiences a restoring force that acts perpendicular to its path of motion.
- ⚖️ The relationship between the restoring force (F) and displacement (x) in SHM is given by F = -kx, where k is the proportionality constant and the negative sign indicates the opposite direction.
- 📉 In the context of a pendulum, the restoring force can be expressed as the product of mass (m) and acceleration (a), leading to the equation ma = -kx.
- 🔢 The acceleration in SHM is the second derivative of the position function with respect to time, which can be expressed as a = (d^2x/dt^2) = -ω^2x, where ω is the angular frequency.
- 🔄 The equation of motion for SHM can be simplified to a second-order differential equation involving velocity and position, dv/dt + ω^2x = 0.
- 🔄 By applying calculus, the relationship between velocity, acceleration, and displacement in SHM can be derived, leading to the equation v = ω√(a^2 - x^2).
- 📈 The position of a particle in SHM over time can be described using the equation x = a sin(ωt + φ), where a is the amplitude, ω is the angular frequency, t is time, and φ is the phase constant.
- 🔑 The phase constant (φ) in SHM represents the initial displacement of the particle from the equilibrium position and is crucial for determining the starting point of the motion.
- 🧭 Understanding the phase constant and its role in SHM is essential for analyzing the complete motion of a particle, including its velocity and position at any given time.
Q & A
What is simple harmonic motion?
-Simple harmonic motion is a type of periodic motion where the restoring force acting on an object is directly proportional to the displacement from its equilibrium position, and the displacement is in the direction of restoring the object to its equilibrium position.
Why is a simple pendulum considered an ideal example of simple harmonic motion?
-A simple pendulum is an ideal example of simple harmonic motion because it exhibits a restoring force that is proportional to its displacement from the equilibrium position, which is a characteristic of simple harmonic systems.
What is the mathematical relationship between the restoring force (F) and displacement (x) in simple harmonic motion?
-In simple harmonic motion, the restoring force (F) is directly proportional to the displacement (x) from the equilibrium position, and since they are in opposite directions, the relationship is given by F = -kx, where k is the proportionality constant.
How is the acceleration (a) of an object in simple harmonic motion related to its displacement (x)?
-The acceleration (a) of an object in simple harmonic motion is related to its displacement (x) through the equation a = -ω²x, where ω is the angular frequency of the motion.
What is the significance of the angular frequency (ω) in the equation of motion for simple harmonic motion?
-The angular frequency (ω) is significant as it represents the rate of change of the phase of the motion. It is defined as the square root of the proportionality constant (k) divided by the mass (m) of the object, and it determines the frequency of oscillation.
How does the velocity (v) of an object in simple harmonic motion relate to its displacement (x)?
-The velocity (v) of an object in simple harmonic motion is related to its displacement (x) through the equation v = ω * sqrt(A² - x²), where A is the amplitude of the motion.
What is the general equation for the position of an object in simple harmonic motion?
-The general equation for the position of an object in simple harmonic motion is x(t) = A * sin(ωt + φ), where A is the amplitude, ω is the angular frequency, t is the time, and φ is the phase constant.
What is the role of the phase constant (φ) in the equation of simple harmonic motion?
-The phase constant (φ) in the equation of simple harmonic motion represents the initial displacement of the particle from the equilibrium position at time t = 0, and it defines the starting phase of the oscillation.
How can the equation for velocity in simple harmonic motion be derived from the position equation?
-The velocity equation in simple harmonic motion can be derived from the position equation by differentiating the position function with respect to time, giving v(t) = dx/dt = Aω * cos(ωt + φ).
What happens to the velocity of a simple pendulum bob at its maximum displacement?
-At the maximum displacement, the velocity of the simple pendulum bob is zero because it momentarily stops before changing direction and starting its return motion towards the equilibrium position.
How can the equation of motion for simple harmonic motion be integrated to find the position as a function of time?
-The equation of motion for simple harmonic motion can be integrated by separating variables and integrating both sides, which leads to the position function x(t) in terms of the inverse sine function and the angular frequency, amplitude, and phase constant.
Outlines
🔍 Introduction to Simple Harmonic Motion
This paragraph introduces the concept of simple harmonic motion (SHM), a type of periodic motion where the restoring force is directly proportional to the displacement from the equilibrium position. The simple pendulum is used as an example to illustrate SHM. The mathematics behind SHM is explained, starting with the proportionality of force (F) to displacement (x), represented as F = -kx, where k is the proportionality constant. The equation is then related to the mass (m) of the pendulum's bob, leading to the acceleration equation a = (d^2x/dt^2) = -(k/m)x, which is key to understanding SHM. The angular frequency (ω) is defined as the square root of k/m, and the general equation for SHM is derived, setting the foundation for further analysis.
📚 Derivation of SHM Equations and Phase Constant
The second paragraph delves deeper into the mathematical derivation of SHM, starting with the equation for acceleration as the second derivative of the position function. By applying calculus, the relationship between acceleration, velocity, and displacement is established, leading to the equation dv/dt + ω^2x = 0. The integration of this equation, considering the conditions at maximum displacement (where velocity is zero), results in the expression for velocity as a function of position, v = ω√(a^2 - x^2). The position as a function of time is then derived by integrating the velocity equation, which introduces the phase constant (φ) and results in the sinusoidal position function x = a sin(ωt + φ). The phase constant is explained as the initial displacement from the equilibrium, completing the mathematical description of SHM.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Restoring Force
💡Displacement
💡Equilibrium Position
💡Proportionality Constant
💡Mass
💡Acceleration
💡Angular Frequency
💡Velocity Function
💡Amplitude
💡Phase Constant
Highlights
Simple harmonic motion is a special type of periodic motion where the restoring force is directly proportional to its displacement towards the equilibrium position.
A simple pendulum serves as a classic example of a system undergoing simple harmonic motion.
The restoring force in simple harmonic motion is proportional to the displacement and acts in the opposite direction, represented by the equation ( f = -kx ).
In the context of a pendulum, the restoring force can be expressed as ( ma = -kx ), where ( m ) is the mass and ( a ) is the acceleration.
Acceleration in simple harmonic motion is the second derivative of the position function with respect to time.
The angular frequency squared ( ω^2 ) is defined as the proportionality constant ( k ) divided by the mass ( m ) of the system.
The general equation for simple harmonic motion is derived by dividing the restoring force equation by the mass ( m ) and is represented as ( d^2x/dt^2 + ω^2 x = 0 ).
The equation of motion can be simplified by expressing acceleration as the first derivative of the velocity function with respect to time.
The chain rule of calculus is applied to rewrite the equation in terms of velocity and position, leading to ( dv/dx ⋅ v + ω^2 x = 0 ).
By integrating the derived equation, we obtain the relationship between velocity, position, and the integrating constant.
At the maximum displacement (amplitude), the velocity of the pendulum bob is zero, which helps determine the integrating constant.
The equation ( 1/2 v^2 = -1/2 ω^2 x^2 + 1/2 ω^2 a^2 ) relates velocity, position, and amplitude in simple harmonic motion.
The velocity of the system in simple harmonic motion can be expressed as ( v = ω √(a^2 - x^2) ).
To find the position as a function of time, the equation is manipulated to isolate ( dx/dt ) and integrated.
The integration of the position equation leads to an expression involving the inverse sine function and the phase constant.
The phase constant ( φ ) defines the initial displacement of the particle from the equilibrium position in simple harmonic motion.
The final position equation for a particle in simple harmonic motion is ( x = a sin(ω t + φ) ), where ( a ) is the amplitude and ( ω ) is the angular frequency.
Transcripts
Browse More Related Video

Wave Equation
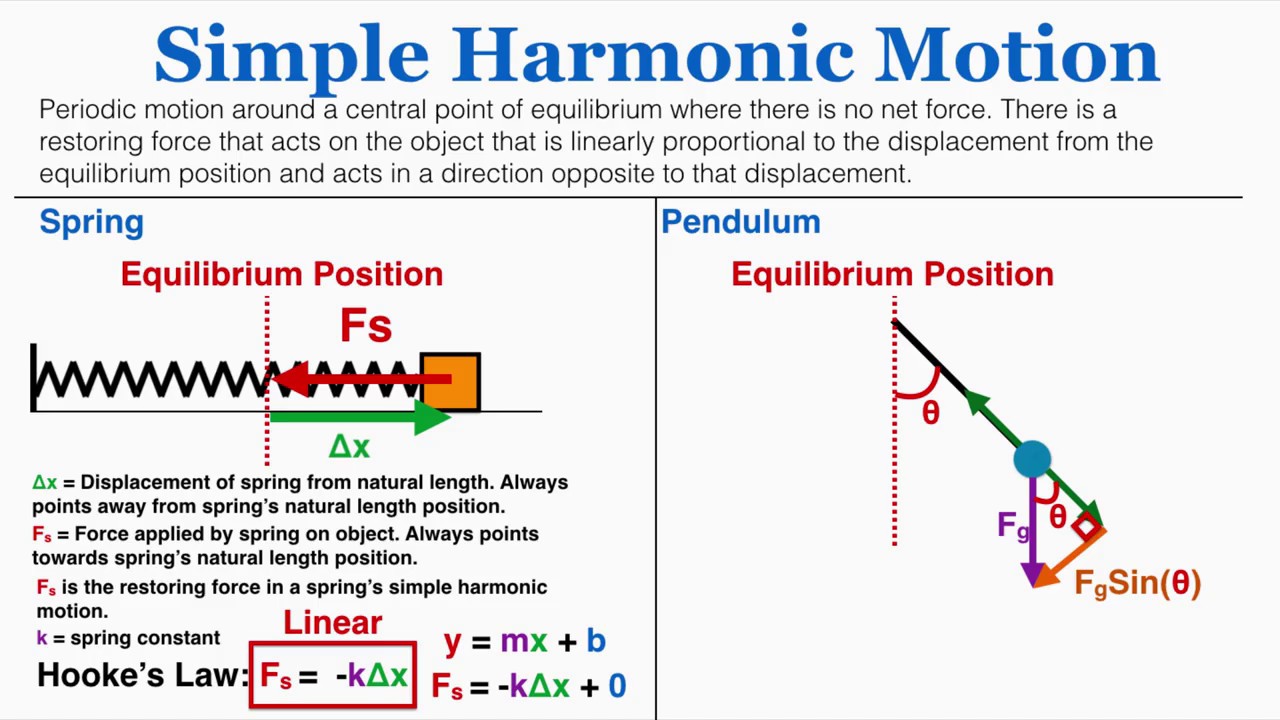
Simple Harmonic Motion - IB Physics

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)

AP Physics 1 - Simple Harmonic Motion
AP Physics Lecture on Simple Harmonic Motion. Watch this before 6.C

Rotational Motion Physics, Basic Introduction, Angular Velocity & Tangential Acceleration
5.0 / 5 (0 votes)
Thanks for rating: