unit 3 review - Circular motion and gravitation
TLDRThis educational script discusses key concepts in physics, focusing on circular motion, gravitation, and their interplay in orbital problems. It explains centripetal acceleration, Newton's second law in the context of circular motion, and clarifies misconceptions about 'centrifugal force.' The script delves into the law of universal gravitation, gravitational fields, and orbital motion, emphasizing the importance of understanding these concepts for exams like the AP. It concludes with the significance of combining equations for circular motion and gravity to solve orbital problems.
Takeaways
- 🔄 Unit 3 focuses on circular motion and gravitation, which are interconnected through orbital problems involving circular motion caused by gravity.
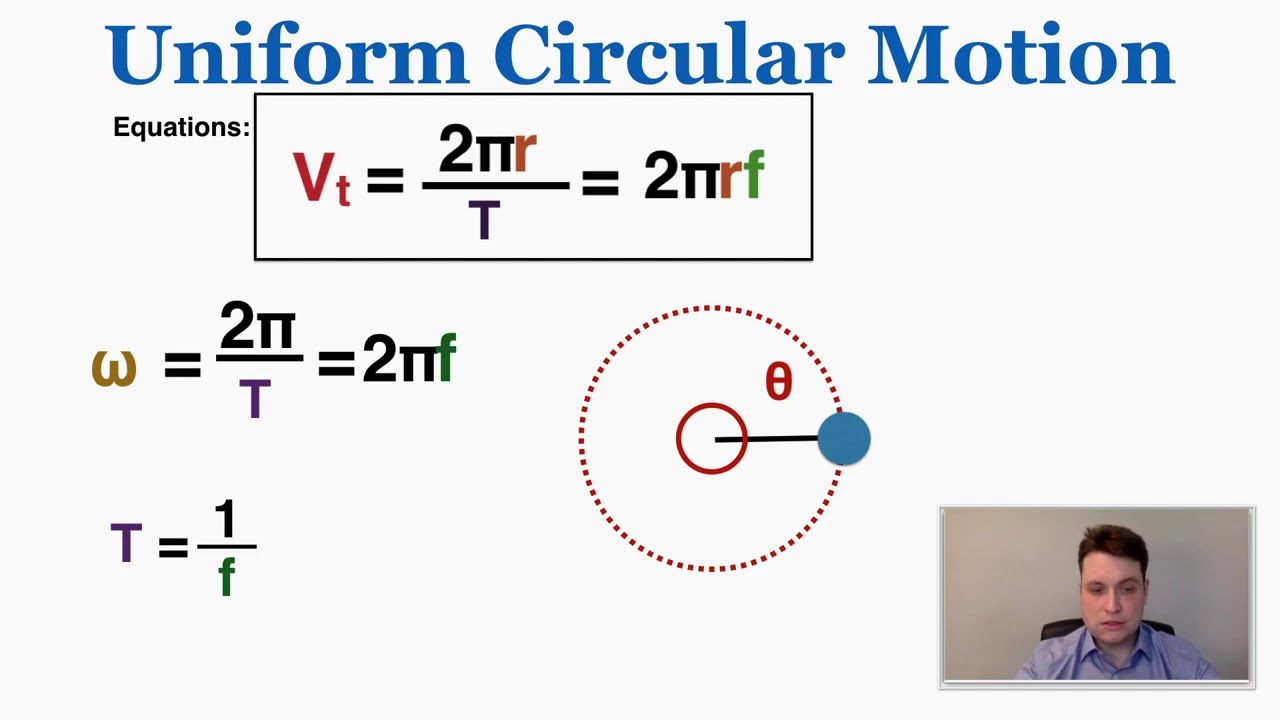
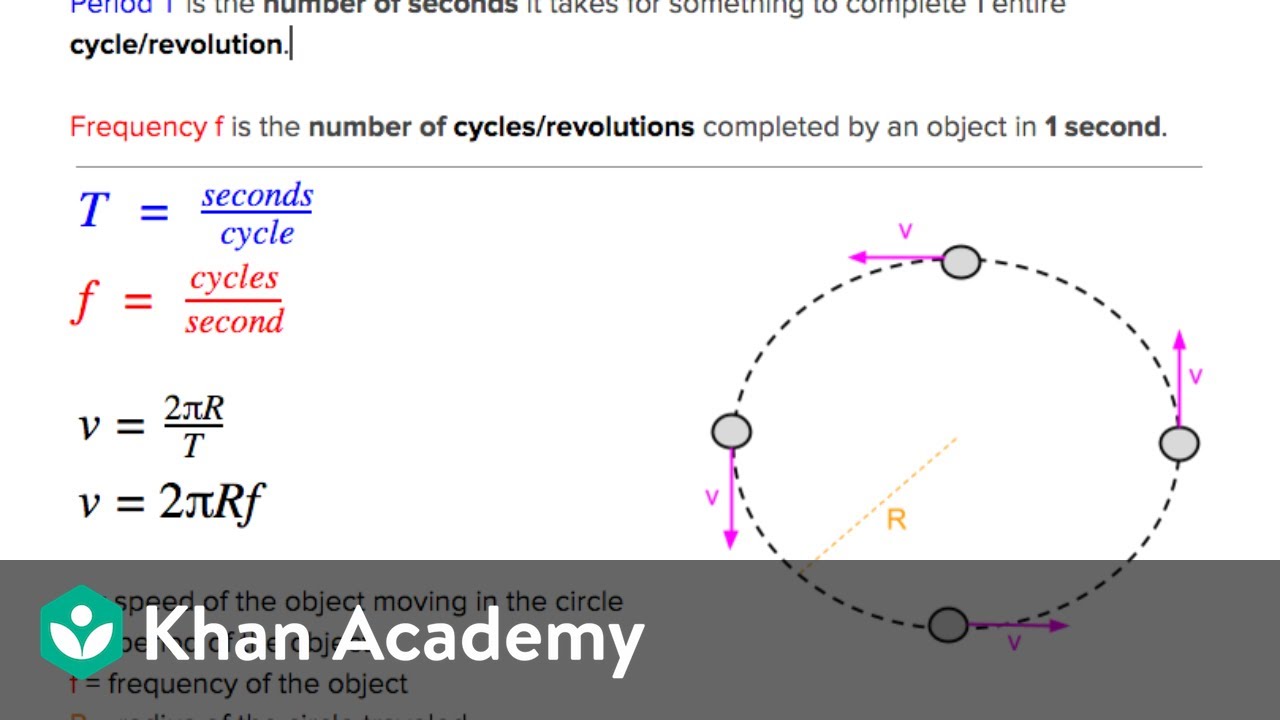
- 📐 In uniform circular motion, the speed is constant, but the direction of velocity changes, resulting in a centripetal acceleration calculated as speed squared divided by the radius.
- 🚀 Tangential acceleration, which affects the speed of an object moving in a circle, is not typically a focus on the AP exam and does not affect the calculation of centripetal acceleration.
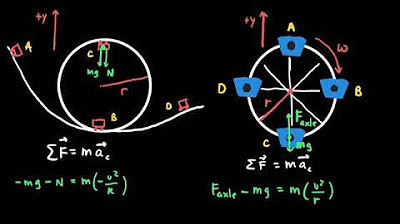
- ⚖️ Newton's second law is applied to centripetal motion, where the net force towards the center of the circle is equal to the mass of the object times the centripetal acceleration.
- 🌐 Centripetal force is always positive as it is directed towards the center of the circle, and the net force in the centripetal direction is calculated by considering forces like tension, gravity, normal force, and friction.
- 🌌 The law of universal gravitation, introduced by Newton, is used to calculate the gravitational force between two masses and involves the gravitational constant G, which is not to be confused with the small g representing acceleration due to gravity.
- 📏 The gravitational force equation uses the center-to-center distance between two objects, which is important for calculating forces when objects are significantly apart, such as the Earth and the Moon.
- 🌍 Gravitational field describes the change in space caused by a mass, affecting the motion of other objects nearby, and is calculated by dividing the gravitational force by the mass of the object at a particular location.
- 🛰 Orbital motion is a type of circular motion where the force toward the center is gravitational, and understanding this relationship is crucial for solving problems on the AP exam.
- 🔁 The orbital period equation relates the distance from the central object, the mass of the central object, and the time it takes an object to complete one orbit.
- 🧠 The AP exam expects students to conceptually understand the combination of circular motion and gravity, and to apply this understanding to derive equations for orbital motion without being explicitly given these equations.
Q & A
What are the key topics covered in Unit 3?
-Unit 3 covers circular motion and gravitation, particularly focusing on orbit problems which involve circular motion caused by gravity.
How is acceleration treated in uniform circular motion?
-In uniform circular motion, speed is constant but acceleration occurs because the direction of velocity changes. The centripetal acceleration is calculated as the speed squared divided by the radius.
What is tangential acceleration and how does it relate to centripetal acceleration?
-Tangential acceleration refers to the change in speed along the circular path, which can be either faster or slower. It does not affect the calculation of centripetal acceleration, which is always directed toward the center of the circle.
How is Newton's Second Law applied in circular motion problems?
-Newton's Second Law in circular motion problems is applied by equating the centripetal acceleration (v^2/r) to the net force toward the center of the circle divided by the mass of the object (F_net/m).
Why is the term 'centrifugal force' considered incorrect?
-The term 'centrifugal force' is considered incorrect because objects do not gain new forces simply by moving in a circle. The correct forces to consider are tension, friction, normal force, and gravity. Centrifugal force is a fictitious force used in a non-inertial frame of reference.
What is the Law of Universal Gravitation?
-The Law of Universal Gravitation states that the gravitational force between two objects is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. The equation is F = G * (m1 * m2) / r^2.
What is the difference between 'big G' and 'little g' in the context of gravitation?
-In the context of gravitation, 'big G' (the gravitational constant) is approximately 6.67 x 10^-11 m^3 kg^-1 s^-2, whereas 'little g' refers to the acceleration due to gravity at the Earth's surface, approximately 9.8 m/s^2.
How is the gravitational field described using the trampoline analogy?
-The gravitational field is described using the trampoline analogy by comparing the effect of a mass on the space around it to a bowling ball on a trampoline. The mass causes a distortion in the space, affecting the motion of other objects, similar to how the bowling ball changes the shape of the trampoline.
How do we calculate the gravitational field strength at a specific location?
-The gravitational field strength at a specific location is calculated by dividing the gravitational force on an object by the mass of that object (g = F/m). If direct measurement is not possible, it can be calculated using the formula g = G * M / r^2, where M is the mass of the object causing the field and r is the distance from its center.
What is the significance of orbital motion in the context of circular motion and gravity?
-Orbital motion is significant because it combines concepts of circular motion and gravity. In orbital problems, the centripetal force is provided by gravity, allowing us to use equations of circular motion (v^2/r) and gravitational force (G * M * m / r^2) together to describe the motion of orbiting objects.
How do we derive the orbital period equation from the concepts of circular motion and gravity?
-The orbital period equation is derived by combining the equations for circular motion and gravitational force. By setting the centripetal force (m * v^2 / r) equal to the gravitational force (G * M * m / r^2) and substituting v with the orbital speed (2 * π * r / T), we can relate the orbital period (T) to the distance from the central object (r) and its mass (M).
Outlines
🔴 Circular Motion and Gravitation
The script begins by discussing the relationship between circular motion and gravitation, particularly in the context of orbits. It explains the concept of centripetal acceleration, which is the acceleration directed towards the center of a circular path, and how it can be calculated using the formula speed squared divided by the radius. The script also touches on tangential acceleration, which is not typically a focus on the AP exam, but is important for understanding changes in speed along the circular path. The discussion then moves to Newton's second law, applying it to centripetal motion and emphasizing that the direction towards the center is always considered positive. The script clarifies misconceptions about centrifugal force, explaining that it is a fictitious force and not a real interaction between objects, and that it arises in non-inertial frames of reference.
🌌 Understanding Gravity and Gravitational Fields
This paragraph delves into the law of universal gravitation, highlighting the importance of distinguishing between the gravitational constant (big G) and the acceleration due to gravity on Earth (little g). It explains the formula for calculating the gravitational force between two objects, emphasizing the significance of using the center-to-center distance rather than surface-to-surface distance. The script also introduces the concept of gravitational field, which describes the change in space caused by a nearby mass, and how it can be measured by dividing the gravitational force by the mass of an object at a specific location. The gravitational field is a property of space, and the script illustrates this with analogies like a bowling ball on a trampoline, indicating how the presence of mass alters the space around it and affects the motion of other objects.
🚀 Orbital Motion and Its Relation to Circular Motion and Gravity
The script discusses orbital motion, often considered as a form of circular motion influenced by gravity. It points out that while orbits may not be perfectly circular, for celestial bodies like planets and moons, they are close enough to be treated as such for most calculations. The script emphasizes the conceptual understanding required to combine equations of circular motion and gravity, as the AP exam does not provide derived equations for orbital motion. By substituting the centripetal force with the gravitational force equation, the script derives an equation for the velocity of an orbiting object in terms of the mass of the central object and the radius of the orbit. It also explains how to relate the velocity to the orbital period by considering the circumference of the orbit and the time it takes to complete one orbit.
Mindmap
Keywords
💡Circular Motion
💡Centripetal Acceleration
💡Tangential Acceleration
💡Newton's Second Law
💡Gravitation
💡Law of Universal Gravitation
💡Gravitational Field
💡Orbital Motion
💡Centrifugal Force
💡Orbital Period
Highlights
Unit 3 combines circular motion and gravitation, illustrating how they work together in orbit problems.
In uniform circular motion, the speed is constant, but the direction of velocity changes, resulting in centripetal acceleration.
The formula for centripetal acceleration is speed squared divided by the radius of the circle.
Tangential acceleration, which can occur when an object is speeding up or slowing down in a circle, does not affect the calculation of centripetal acceleration.
Newton's second law is applied to centripetal motion by equating the net force towards the center of the circle to the mass times the centripetal acceleration.
The concept of centripetal force is always positive and directed towards the center of the circle, regardless of the actual direction of forces involved.
Centrifugal force is not a real force; it is a fictitious force introduced in non-inertial frames of reference to explain motion.
The law of universal gravitation, introduced by Newton, quantifies the gravitational force between two masses.
The gravitational constant, G, is distinct from the acceleration due to gravity, g, and has a value of 6.67 x 10^-11 m^3 kg^-1 s^-2.
The gravitational force equation uses the center-to-center distance between two objects, not the surface-to-surface distance.
Gravitational field describes the change in space caused by a mass, often visualized with analogies like a bowling ball on a trampoline.
The gravitational field strength at a location is calculated by dividing the gravitational force at that location by the mass of an object there.
Orbital motion is a type of circular motion where the centripetal force is provided by gravity.
The orbital period equation relates the distance from the central object, the mass of the central object, and the time it takes for an object to complete one orbit.
On the AP exam, students are expected to understand the conceptual relationship between circular motion and gravity without memorizing derived orbital motion equations.
The mass of the object in orbit is irrelevant to its orbital period; only the mass of the central object and the distance from it matter.
Transcripts
Browse More Related Video

2022 Live Review 3 | AP Physics 1 | Understanding Circular Motion and Gravitation
AP Physics 1 Circular Motion and Gravitation Review
Uniform Circular Motion - IB Physics
AP Physics 1 review of Centripetal Forces | Physics | Khan Academy

AP Physics Workbook 3.M Gravitational Fields

AP Physics Workbook 3.O The Gravitational Force
5.0 / 5 (0 votes)
Thanks for rating: