Higher order derivatives | Chapter 10, Essence of calculus

3Blue1Brown
7 May 201705:38
EducationalLearning
32 Likes 10 Comments

TLDRThis script introduces higher order derivatives, focusing on the second derivative to explain its significance in the context of graphs and motion. The second derivative, denoted as d²f/dx², measures how the slope of a function changes, indicating whether the function is curving upwards (positive) or downwards (negative). It is also related to acceleration in physics, with the third derivative known as 'jerk', which signifies changes in acceleration. The script highlights the utility of higher order derivatives in approximating functions, setting the stage for the upcoming discussion on Taylor series.

Takeaways
  • 📚 The next chapter will focus on Taylor series and frequently reference higher order derivatives.
  • 🚀 If you're already familiar with second, third, and higher order derivatives, you can skip ahead to the main content.
  • 🔍 The script introduces higher order derivatives for those who haven't encountered them yet, aiming for completeness.
  • 📈 The first derivative of a function can be interpreted as the slope of the graph at a point, with steepness indicating the derivative's value.
  • 📉 The second derivative is the derivative of the first derivative, indicating how the slope is changing.
  • 📊 A positive second derivative at a point means the slope is increasing, suggesting upward curvature of the graph.
  • 📈 Conversely, a negative second derivative indicates the slope is decreasing, showing downward curvature.
  • 📝 The notation for the second derivative is typically written as \( \frac{d^2f}{dx^2} \), representing the rate of change of the first derivative.
  • 🔧 The concept of second derivative can be understood through the analogy of a function's change over small increments of \( x \).
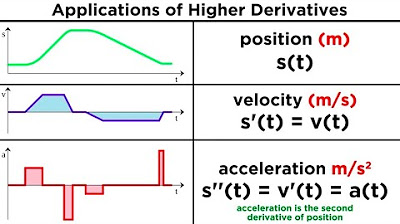
  • 🏎 In the context of motion, the second derivative represents acceleration, showing how the velocity is changing over time.
  • 🤔 The third derivative, humorously called 'jerk', indicates changes in the strength of acceleration.
  • 🛠 Higher order derivatives are useful in approximating functions, which is a key topic in the upcoming discussion on Taylor series.
Q & A

  • What is the primary interpretation of the derivative of a function?

    -The derivative of a function can be interpreted as the slope of the graph of the function at a given point. A steep slope indicates a high value for the derivative, while a downward slope means a negative derivative.

  • What does the second derivative represent?

    -The second derivative represents the derivative of the derivative, which means it tells you how the slope of the function's graph is changing. It indicates whether the slope is increasing or decreasing.

  • How can you visually determine the sign of the second derivative from the graph of a function?

    -At points where the graph curves upwards, the slope is increasing, indicating a positive second derivative. Conversely, at points where it curves downwards, the slope is decreasing, indicating a negative second derivative. If there's no curvature, the second derivative is zero.

  • What is the standard notation for the second derivative?

    -The standard notation for the second derivative is d²f/dx², which is an abbreviation for the derivative of the derivative function with respect to x.

  • Can you explain the concept of 'ddf' in the context of the second derivative?

    -The 'ddf' refers to the difference in the change of the function after taking two small steps to the right, each of size dx. It represents the change in how the function changes and is proportional to the square of the size of dx (dx²).

  • How does the second derivative relate to the concept of acceleration in physics?

    -The second derivative is analogous to acceleration in physics. Given a function that records distance traveled versus time, the second derivative represents the rate at which the velocity (the first derivative) is changing.

  • What is the term used for the third derivative of a function?

    -The third derivative of a function is called 'jerk'. It represents the rate at which the acceleration (the second derivative) is changing.

  • What is the practical application of higher order derivatives in approximating functions?

    -Higher order derivatives are useful in approximating functions because they provide information about the behavior of the function beyond just the slope and curvature. They help in understanding the rate of change of these properties, which is essential in techniques like Taylor series expansion.

  • How does a positive second derivative affect the motion of an object?

    -A positive second derivative indicates that the object is speeding up, as it suggests that the velocity is increasing. This can be felt as a sensation of being pushed back into a car seat or having the car seat push you forward.

  • What does a negative second derivative signify in terms of motion?

    -A negative second derivative signifies that the object is slowing down, which means the velocity is decreasing. This is also referred to as negative acceleration.

  • How does the concept of 'jerk' relate to the physical world?

    -In the physical world, 'jerk' is the third derivative of a function that describes motion. If the jerk is not zero, it means that the strength of the acceleration is changing, which can be felt as a change in the pushing or pulling force acting on an object.

Outlines
00:00
📈 Understanding Higher Order Derivatives

This paragraph introduces the concept of higher order derivatives, specifically focusing on the second derivative. It explains the second derivative as the derivative of the derivative, which indicates how the slope of a function's graph is changing. The text uses visual analogies, such as the curvature of the graph and the direction of the slope, to illustrate when the second derivative would be positive, negative, or zero. Notation for the second derivative is also discussed, with a step-by-step explanation of how to interpret the standard notation \( d^2f/dx^2 \). The concept of acceleration as it relates to the second derivative in the context of motion is introduced, and the third derivative, humorously referred to as 'jerk,' is mentioned as a measure of how the acceleration is changing. The paragraph concludes by highlighting the importance of higher order derivatives in approximating functions, which is a topic that will be further explored in the next chapter on Taylor series.

05:06
🔍 Approximating Functions with Higher Order Derivatives

The second paragraph briefly mentions the utility of higher order derivatives in approximating functions, which is the main subject of the upcoming chapter on Taylor series. It serves as a transition, indicating that the detailed exploration of how higher order derivatives aid in function approximation will be covered in the next chapter. This paragraph acts as a teaser, building anticipation for the material to come and reinforcing the significance of the concepts introduced in the first paragraph.

Mindmap
Keywords
💡Taylor series
The Taylor series is a mathematical representation of a function as an infinite sum of terms calculated from the values of its derivatives at a single point. It is a key concept in the video as it is the main topic of the next chapter, which the video is introducing. The Taylor series is used to approximate functions, which is central to the discussion of higher order derivatives in the context of the video.
💡Higher order derivatives
Higher order derivatives refer to the derivatives of a function beyond the first order. In the video, they are discussed in the context of understanding how the slope of a function's graph changes, which is crucial for comprehending the motion and acceleration of an object. The second derivative, for instance, indicates how the rate of change of the slope is varying.
💡Second derivative
The second derivative of a function is the derivative of the first derivative. It measures how the slope of the graph of the function is changing. In the video, it is used to describe the curvature of the graph and the rate of change of velocity, which is directly related to acceleration. For example, a positive second derivative indicates that the slope is increasing, while a negative one indicates that the slope is decreasing.
💡Derivative
The derivative of a function at a chosen point is the slope of the tangent line to the graph of the function at that point. It is a fundamental concept in calculus and is used in the video to explain the rate of change of a quantity. The derivative is also the basis for understanding higher order derivatives, such as the second and third derivatives, which are discussed in the video.
💡Graph
A graph is a visual representation of a function, showing the relationship between the input and output variables. In the video, graphs are used to illustrate the concepts of derivatives, showing how the slope of the graph changes and how this relates to the function's behavior. The graph's curvature is particularly important for understanding the second derivative.
💡Slope
Slope is a measure of the steepness of a line, or in the context of the video, the steepness of the tangent line to a curve at a particular point. It is defined as the change in the 'y' value divided by the change in the 'x' value. In the video, the slope is used to describe the rate at which a function's graph rises or falls, which is central to understanding the concept of the derivative.
💡Motion
Motion refers to the movement of an object along a path. In the video, motion is discussed in relation to the distance traveled over time, with the function's graph representing this distance. The derivatives of this function are used to describe the velocity and acceleration of the object, making motion a key example for illustrating the practical application of derivatives.
💡Velocity
Velocity is the rate of change of an object's position with respect to time. It is a physical quantity that is derived from the first derivative of the position function. In the video, velocity is used as an example to explain how the first derivative of a function can represent the rate of change of a quantity over time.
💡Acceleration
Acceleration is the rate of change of velocity with respect to time. It is a physical quantity that describes how quickly the velocity of an object is changing. In the video, acceleration is derived from the second derivative of the position function and is used to illustrate how the rate of change of velocity can be represented mathematically.
💡Jerk
Jerk, in physics, is the rate of change of acceleration with respect to time, or the third derivative of the position function. It is used in the video to describe the change in the strength of acceleration. The concept of jerk is introduced humorously to highlight the importance of higher order derivatives in understanding the nuances of motion.
💡Approximation
Approximation in mathematics is the process of finding a value that is close to the actual value but is easier to use or calculate. In the video, approximation is discussed in the context of using higher order derivatives to approximate functions, particularly through the use of Taylor series. This is important for simplifying complex calculations and understanding the behavior of functions over a range of values.
Highlights

Frequent reference to higher order derivatives in the next chapter on Taylor series

If comfortable with second, third derivatives, feel free to skip ahead

Higher order derivatives not discussed yet in the series

Quick overview of higher order derivatives for completeness

Focus on second derivative in context of graphs and motion

Derivative interpreted as slope of graph above a point

Second derivative is derivative of the derivative, tells how slope is changing

Second derivative positive when graph curves upward, negative when curving downward

Second derivative = 0 when no curvature

Notation: d^2f/dx^2 for second derivative

Intuition for second derivative through small steps and changes in function

Second derivative represents acceleration in distance vs time graphs

Third derivative called jerk, measures how acceleration itself is changing

Higher order derivatives useful for approximating functions

Second derivative positive = speeding up, negative = slowing down

Taylor series chapter will explore higher order derivatives further

Transcripts

Browse More Related Video

Calculus - Lesson 11 | Derivative as a Function | Don't Memorise

Higher Derivatives and Their Applications

BusCalc 18 Second Derivatives

Higher Derivatives and Concavity

Calculus 1 Lecture 3.4: The Second Derivative Test for Concavity of Functions

Lesson 6 - Higher Derivatives in Calculus (Calculus 1 Tutor)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DerivativesSecond DerivativeGraph InterpretationMotion AnalysisAccelerationJerkFunction ApproximationTaylor SeriesMathematicsEducational