Calculus - Lesson 11 | Derivative as a Function | Don't Memorise
TLDRThis video script explores the concept of derivatives in calculus, explaining how the derivative of a function yields a new function, the derived function, which represents the slope of the tangent line at any point on the original function's graph. It delves into the domain of derived functions, highlighting that it's limited to where the derivative exists. The script further discusses higher-order derivatives, emphasizing the significance of the second derivative in physics, as it represents acceleration and the force acting on an object. The video also clarifies the notation used for derivatives, illustrating it as the ratio of infinitesimal changes, despite being a limit, not an actual ratio.
Takeaways
- 📚 The derivative of a function is itself a function, which is referred to as the derived function.
- 🔍 The derived function, denoted by y' or f'(x), represents the slope of the tangent line at a particular point on the original function.
- 📉 The domain of the derived function includes all values of x for which the derivative exists within the domain of the original function.
- 🚫 There are instances where the derived function is not defined, such as at points where the derivative does not exist.
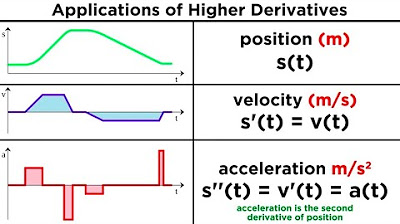
- 🔢 Higher-order derivatives, such as the second, third, and fourth derivatives, can be found by differentiating the derived function multiple times.
- 🏎 The second derivative of a position function in physics represents acceleration, which is the rate of change of speed over time.
- 🔧 The second derivative also indicates the force acting on an object, as per Newton's second law of motion (force equals mass times acceleration).
- 📈 The significance of higher-order derivatives becomes more apparent in advanced calculus topics.
- 📝 The notation dy/dx or df/dx for derivatives is used to represent the limit of the ratio of infinitesimal changes in y and x, not an actual ratio.
- 🤔 The concept of derivatives is not just about finding a ratio but understanding the limit process and the instantaneous rate of change.
- 💬 The script encourages viewers to share their thoughts on derivative notations and to continue learning calculus by subscribing to the channel.
Q & A
What is the derivative of a function?
-The derivative of a function is a measure of the rate at which the function's value changes with respect to changes in its variable. It represents the slope of the tangent line to the function's graph at a particular point.
Is the derivative of a function also a function?
-Yes, the derivative of a function is itself a function. It assigns a new value, which is the slope of the tangent line at each point of the original function.
What is the derived function?
-The derived function is the new function obtained after finding the derivative of the original function. It relates each value of the independent variable x to the derivative of the original function at that point.
What determines the domain of the derived function?
-The domain of the derived function is determined by the set of all values of the independent variable x for which the derivative of the original function exists and is defined.
Can the derived function have points where it is not defined?
-Yes, the derived function can have points where it is not defined, particularly at values of x where the original function's derivative does not exist.
What is the significance of higher-order derivatives?
-Higher-order derivatives, such as the second, third, and fourth derivatives, provide additional information about the function's behavior, such as concavity, inflection points, and higher-order rates of change.
What does the second derivative represent in the context of motion?
-In the context of motion, the second derivative represents acceleration, which is the rate of change of speed with respect to time.
How is the second derivative related to force in physics?
-According to Newton's second law of motion, force is equal to mass times acceleration. Therefore, the second derivative of an object's position function with respect to time gives the force acting on the object.
What does the notation dy/dx signify?
-The notation dy/dx represents the derivative of a function y with respect to x. It is a way to express the rate of change of y for an infinitesimal change in x.
Why is the dy/dx notation useful in calculus?
-The dy/dx notation is useful because it captures the intuitive idea of the derivative as the ratio of infinitesimal changes in y and x, helping to visualize how the value of y changes with a small change in x.
Can the derived function be differentiated further?
-Yes, the derived function can be differentiated further to obtain higher-order derivatives, which can provide deeper insights into the function's behavior.
Outlines
📚 Understanding Derivatives and Derived Functions
This paragraph introduces the concept of derivatives and how they represent the slope of the tangent line at a particular point on a function. It explains that the derivative of a function itself becomes a new function, which is called the derived function. The paragraph uses the example of the function y = x^2 to illustrate how the derivative at any point x is represented by 2x, and that this relationship defines a new function y'. It also discusses the domain of the derived function, which is the set of all x values for which the derivative exists. The example of the function defined at x=0 but without a derivative at that point is used to clarify this concept. Finally, the paragraph raises the question of whether the derived function can be differentiated again, hinting at the possibility of higher-order derivatives.
🔍 Exploring Higher-Order Derivatives and Their Significance
The second paragraph delves into higher-order derivatives, which are obtained by differentiating the derived function multiple times. It explains that these derivatives can provide significant insights, especially in advanced calculus topics, and uses the second derivative as an example to discuss its importance in physics. The paragraph explains how the second derivative of a position function with respect to time gives the acceleration of an object, which is the rate of change of speed. It further connects this concept to Newton's second law of motion, where force is equal to mass times acceleration, thus showing that the second derivative of the position function can reveal the force acting on an object. The paragraph also touches on the various notations used to represent derivatives and their implications in understanding the concept of derivatives as limits rather than ratios.
📘 Derivative Notation and Infinitesimal Changes
The final paragraph focuses on the notation used for derivatives, particularly the dy/dx notation, and its intuitive interpretation. It clarifies that while the notation suggests a ratio, the derivative is actually a limit of such a ratio, not a ratio itself. The paragraph uses the concept of infinitesimal changes (denoted by dx and dy) to explain how the derivative can be thought of as the ratio of these infinitesimals, indicating how y changes with respect to an infinitesimally small change in x. This explanation aims to provide an intuitive understanding of the derivative as it relates to the instantaneous rate of change. The paragraph concludes by inviting viewers to share their thoughts on derivative notation and to continue learning calculus by subscribing to the channel.
Mindmap
Keywords
💡Derivative
💡Tangent Line
💡Function
💡Independent Variable
💡Dependent Variable
💡Domain
💡Second Derivative
💡Higher-Order Derivatives
💡Instantaneous Rate of Change
💡Notation
Highlights
Derivatives provide a new function that represents the slope of the tangent line at any point on the original function.
The derived function, denoted by y' or f'(x), is a function where y' is the derivative of f(x) at a particular point x.
The domain of the derived function is the set of all x values for which the original function's derivative exists.
Even if a function is defined at a certain point, its derivative might not exist there, affecting the domain of the derived function.
The concept of higher-order derivatives, such as the second, third, and fourth derivatives, can be explored beyond the first derivative.
Higher-order derivatives have significance and applications in advanced calculus topics.
The second derivative of a position function in physics represents acceleration, which is the rate of change of speed over time.
Acceleration can be found by differentiating the speed function, which is the first derivative of the position function.
The second derivative is crucial in understanding the motion of objects and the forces acting upon them, according to Newton's second law.
The notation dy/dx or df/dx for derivatives, while not a ratio, is a useful representation to understand the concept of the derivative.
The derivative can be thought of as the ratio of infinitesimal changes in y and x, denoted by dy and dx respectively.
Differentiating the derived function (f'(x)) itself can lead to further insights, such as the second derivative.
The process of finding the derivative involves taking the limit of the ratio of the change in the dependent variable to the change in the independent variable as the latter approaches zero.
The example of the function y = x^2 is used to illustrate the concept of finding the derivative at a particular value x1, which is 2x1.
The domain of the original function does not necessarily encompass all points where the derived function is defined.
The graph of the derived function for y = x^2 shows that x=0 is not in its domain because the derivative at x=0 does not exist.
Differentiation is a fundamental process in calculus that allows us to find rates of change and slopes of tangent lines.
The video aims to explain the concept of derivatives and their implications in understanding the behavior of functions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: