Calculus 1 Lecture 3.4: The Second Derivative Test for Concavity of Functions

Professor Leonard

16 Jan 201436:49

EducationalLearning

32 Likes 10 Comments

TLDRThe transcript is a detailed mathematical lecture focusing on the concepts of derivatives and their applications in calculus. It explains the role of the first derivative in determining the slope of a curve and how it can indicate increasing or decreasing functions. The lecture then delves into the significance of the second derivative, which is pivotal in understanding the concavity of a curve, revealing whether the slope is increasing or decreasing. This concept is crucial for identifying inflection points, which are locations where the curve changes concavity. The speaker introduces the 'second derivative test,' a method for finding potential inflection points by setting the second derivative to zero and solving for x. The lecture also covers how to use the first and second derivative tests together to sketch the graph of a function, providing insights into its behavior without the need for a calculator. The summary concludes with a mention of upcoming topics on limits at infinity, which will further enhance the understanding of function behavior as input values extend towards positive or negative infinity.

Takeaways

📈 The first derivative of a function is related to the slope of the tangent line to the curve and can indicate whether the function is increasing or decreasing.
📉 The second derivative of a function is connected to the concavity of the function, showing whether the slope is increasing or decreasing, which helps determine the shape of the curve, whether it is concave up or concave down.
✍️ When the second derivative is positive, the function is concave up, indicating that the slope is increasing. Conversely, a negative second derivative means the function is concave down, indicating a decreasing slope.
🔍 If the second derivative equals zero, it may indicate a potential inflection point, where the concavity of the function could change.
🔑 The second derivative test involves finding the second derivative, setting it equal to zero to find possible inflection points, and then testing intervals to determine the concavity.
📊 The second derivative test complements the first derivative test by providing information about the concavity of the function, which, along with the first derivative test, can give a complete picture of the function's behavior.
🤔 To find inflection points, plug the possible x-values from the second derivative into the original function to find the corresponding y-values, which gives the coordinates of the inflection points.
📐 The first derivative test identifies where the function could have a relative maximum or minimum by finding where the derivative is zero or undefined.
📈📉 The combination of the first and second derivative tests allows for a detailed analysis of a function's graph, including increasing/decreasing intervals and concavity changes.
🌐 The process of curve sketching involves using the first and second derivative tests to visualize and understand the graph of a function without a calculator.
∞ The concept of limits at infinity is introduced as a way to determine the behavior of a function as the input (x) approaches very large values, which can help understand the end behavior of the function.

Q & A

What does the first derivative of a function represent?
-The first derivative of a function represents the slope of the tangent line to the function at a given point. It indicates the rate of change or the increasing and decreasing behavior of the function.
How is the second derivative related to the shape of a curve?
-The second derivative is related to the curvature or concavity of a curve. It indicates how the slope of the function is changing, which can tell us if the curve is concave up (where the slope is increasing) or concave down (where the slope is decreasing).
What is an inflection point?
-An inflection point is a point on a curve where the concavity changes. It is where the function transitions from being concave up to concave down or vice versa.
How does the second derivative test help in identifying inflection points?
-The second derivative test involves setting the second derivative equal to zero and solving for x to find possible inflection points. By testing intervals around these points with the second derivative, one can determine where the concavity changes, indicating an inflection point.
What does it mean if the second derivative of a function is positive?
-If the second derivative is positive, it means the slope of the function is increasing, and the graph of the function is concave up.
What does it mean if the second derivative of a function is negative?
-If the second derivative is negative, it means the slope of the function is decreasing, and the graph of the function is concave down.
What is the purpose of the first derivative test?
-The first derivative test is used to find critical points where the slope of the tangent to the curve is zero or undefined. These points can be local maxima, local minima, or points of inflection.
What is the relationship between the sign of the first derivative and the increasing/decreasing behavior of a function?
-If the first derivative is positive over an interval, the function is increasing on that interval. If the first derivative is negative, the function is decreasing on that interval.
How does the second derivative test complement the first derivative test?
-The second derivative test provides information about the concavity of the function, which, along with the first derivative test, gives a complete picture of the function's behavior, including increasing/decreasing intervals and concavity changes.
What is the significance of a second derivative equal to zero in the context of the second derivative test?
-A second derivative equal to zero is a potential inflection point. However, it is necessary to check the intervals around this point to confirm a change in concavity, which would indicate an actual inflection point.
How can limits at infinity be used to understand the end behavior of a function?
-Limits at infinity allow us to predict the behavior of a function as the input (x-value) becomes extremely large or small, heading towards positive or negative infinity. This can help determine if a function grows without bound, decays to zero, or approaches a certain value as x increases or decreases without limit.

Outlines

00:00

📈 Understanding the Second Derivative and Curve Shape

The first paragraph introduces the concept of the second derivative in relation to the change in slope, which is pivotal in determining the shape of a curve, whether it is concave up or down. It explains that a positive second derivative indicates an increasing slope and a concave up shape, while a negative second derivative points to a decreasing slope and a concave down shape. The possibility of an inflection point, where concavity changes, is also discussed, which occurs when the second derivative equals zero. The second derivative test is introduced as a method to find inflection points by setting the second derivative to zero and solving for the variable.

05:14

📊 Applying the Second Derivative Test to Identify Inflection Points

The second paragraph delves into the application of the second derivative test. It outlines the process of finding possible inflection points by setting the second derivative to zero and solving for the variable. The importance of testing intervals around the solutions to determine concavity is emphasized. The paragraph also explains how to create a second derivative table and how it complements the first derivative test by providing a comprehensive understanding of a graph's behavior, including increasing/decreasing trends, relative maxima/minima, and inflection points.

10:15

🔍 Identifying Inflection Points with the Second Derivative Test

This paragraph focuses on the practical application of the second derivative test to find inflection points. It guides through taking the second derivative, setting it to zero, and solving for possible inflection points. The process of creating a second derivative table and checking intervals to determine the concavity is detailed. The paragraph emphasizes the significance of the second derivative in assessing concavity changes and how it can indicate inflection points, which are essential for understanding the graph's overall shape.

15:15

🧮 Calculating the Second Derivative and Finding Inflection Points

The fourth paragraph continues the discussion on finding inflection points by taking the second derivative of a given function. It explains the process of solving the second derivative equal to zero to find possible inflection points and emphasizes the need to check intervals to determine the actual points of concavity change. The paragraph also clarifies the use of the original function to find the exact coordinates of the inflection points once the x-values are identified.

20:15

🔢 Analyzing the Second Derivative for Concavity and Inflection Points

In this paragraph, the focus is on analyzing the second derivative to understand concavity and identify inflection points without obtaining a numerical value. It discusses the implications of the numerator and denominator of the second derivative on concavity and how undefined points can indicate a change in concavity. The creation of a table to check intervals and determine concavity is also covered, leading to the identification of an inflection point where the concavity changes from up to down.

25:16

📉 Conducting the First and Second Derivative Tests

The sixth paragraph introduces the concept of combining the first and second derivative tests to analyze a function's behavior comprehensively. It outlines finding critical numbers using the first derivative, creating a table to determine intervals of increasing and decreasing, and using the second derivative to assess concavity. The paragraph emphasizes the importance of interpreting the results to understand the graph's overall shape, including its increasing/decreasing nature and concavity.

30:18

🔍 Finalizing the Derivative Tests to Determine Function Behavior

The seventh paragraph concludes the discussion on derivative tests by emphasizing the need to find the exact points of relative maxima, minima, and inflection points. It guides through plugging critical numbers into the original function to find these points' y-values. The paragraph also touches on the next topic of limits at infinity, which is crucial for understanding a function's behavior as it approaches extreme values.

35:21

🌌 Limits at Infinity and Their Role in Function Analysis

The final paragraph shifts the focus to limits at infinity, which are essential for understanding a function's behavior over an infinite domain. It discusses how to determine if a function tends towards a specific number, keeps increasing, or keeps decreasing as it approaches infinity. This concept is crucial for a complete analysis of a function's graph, especially when considering its long-term behavior.

Mindmap

Keywords

💡Derivative

A derivative in calculus represents the rate at which a quantity is changing at a given point. It is the fundamental concept used to discuss the slope of a curve at any point. In the video, the first derivative is associated with increasing and decreasing functions, while the second derivative is linked to the concept of concavity.

💡Slope

Slope refers to the steepness or gradient of a line. In the context of the video, it is used to describe whether a function is increasing or decreasing. The concept of slope is central to understanding how the first derivative of a function can indicate changes in the function's behavior.

💡Second Derivative

The second derivative of a function is the derivative of the first derivative. It provides information about how the slope of the function is changing. The video explains that a positive second derivative indicates that the slope is increasing, leading to a concave up shape, while a negative second derivative indicates a decreasing slope, resulting in a concave down shape.

💡Concavity

Concavity describes the curvature of a function. A function is said to be concave up on an interval if the graph of the function lies above its tangent lines on that interval. Conversely, it is concave down if the graph lies below the tangent lines. The video uses concavity to discuss the shape of the graph of a function in relation to the sign of the second derivative.

💡Inflection Point

An inflection point is a point on the graph of a function where the concavity changes. The video explains that the second derivative being equal to zero is a potential indicator of an inflection point. If the concavity changes from concave up to concave down or vice versa at a point, that point is an inflection point.

💡Second Derivative Test

The second derivative test is a method used to determine the concavity of a function and to find inflection points. The video describes the process of setting the second derivative equal to zero to find possible inflection points and then testing intervals around these points to determine the change in concavity.

💡Critical Numbers

Critical numbers are the values of the independent variable (often x) at which the derivative of a function changes sign. In the video, critical numbers are found by setting the first derivative equal to zero, which helps identify potential relative maxima, minima, and points of inflection.

💡Relative Extrema

Relative extrema refer to points on a function where the function reaches a local maximum or minimum, also known as relative maximum or minimum. The video discusses how the first derivative test can be used to find these points by identifying where the slope of the tangent to the curve is zero.

💡Limits at Infinity

Limits at infinity involve evaluating the behavior of a function as the input (usually x) approaches very large or very small values. The video mentions that this concept will be explored further in the context of determining the end behavior of a function as x approaches positive or negative infinity.

💡Curve Sketching

Curve sketching is the process of drawing the graph of a function based on its derivatives and other properties. The video outlines how the first and second derivative tests can be used to sketch the curve of a function, indicating not just the function's increasing and decreasing intervals but also its concavity and inflection points.

💡General Power Rule

The general power rule is a basic rule in calculus for finding the derivative of a function. It states that the derivative of x^n, where n is any real number, is n*x^(n-1). The video uses this rule to find the first and second derivatives of functions, which are then used to analyze the functions' behavior.

Highlights

The first derivative is related to slope, which is associated with the increase or decrease of a function.

The second derivative represents how the slope is changing, indicating whether it is increasing or decreasing, and thus the shape of the curve, whether it is concave up or down.

A positive second derivative indicates a slope that is increasing, resulting in a concave up shape.

A negative second derivative signifies a slope that is decreasing, leading to a concave down shape.

If the second derivative equals zero, it could indicate a change in concavity, which might be an inflection point.

An inflection point is where the function switches from concave up to concave down or vice versa.

The second derivative test involves finding the second derivative, setting it to zero, and solving for possible inflection points.

After finding possible inflection points, one must test intervals using the second derivative to determine concavity changes.

The second derivative test provides a comprehensive understanding of a function's behavior, including increasing/decreasing and concavity.

To find inflection points, plug in the x-values of possible inflection points into the original function.

The first derivative test is used to find relative maxima and minima, while the second derivative test identifies inflection points.

The first derivative test and second derivative test can be combined to sketch the graph of a function without a calculator.

The first derivative gives information on increasing/decreasing behavior, and the second derivative provides concavity information.

When performing the second derivative test, it is crucial to check the sign of the second derivative in different intervals to determine concavity.

The second derivative test can handle complex functions and is a fundamental step in curve sketching.

The process of finding inflection points and understanding concavity is essential for comprehensively analyzing a function's graph.

The second derivative test is a powerful tool for understanding the behavior of a function, including its shape and changes in concavity.

Transcripts

Browse More Related Video

3.2 - Using Second Derivatives to Classify Max and Min Values

Business Calculus - Math 1329 - Section 3.2 - Concavity and Points of Inflection

Math 11 - Section 3.2

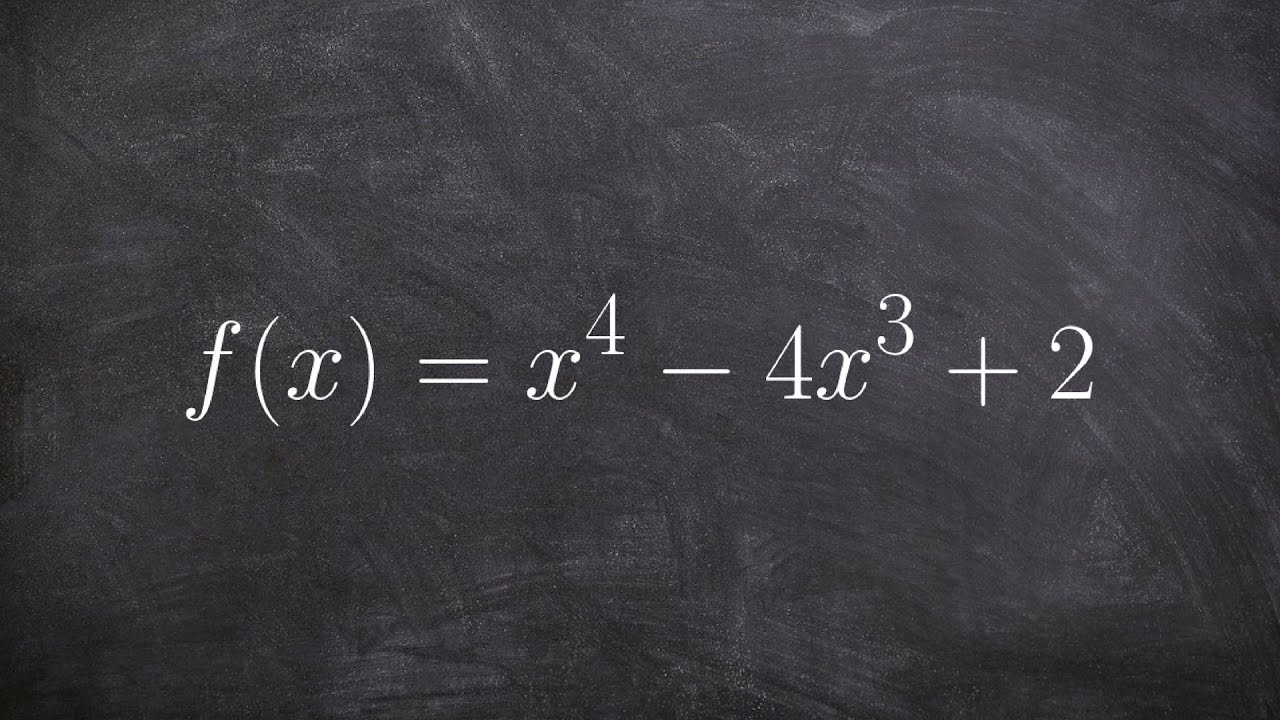
Learn how to determine concavity and point of inflection AP style

What the Second Derivative Tells You about a Graph

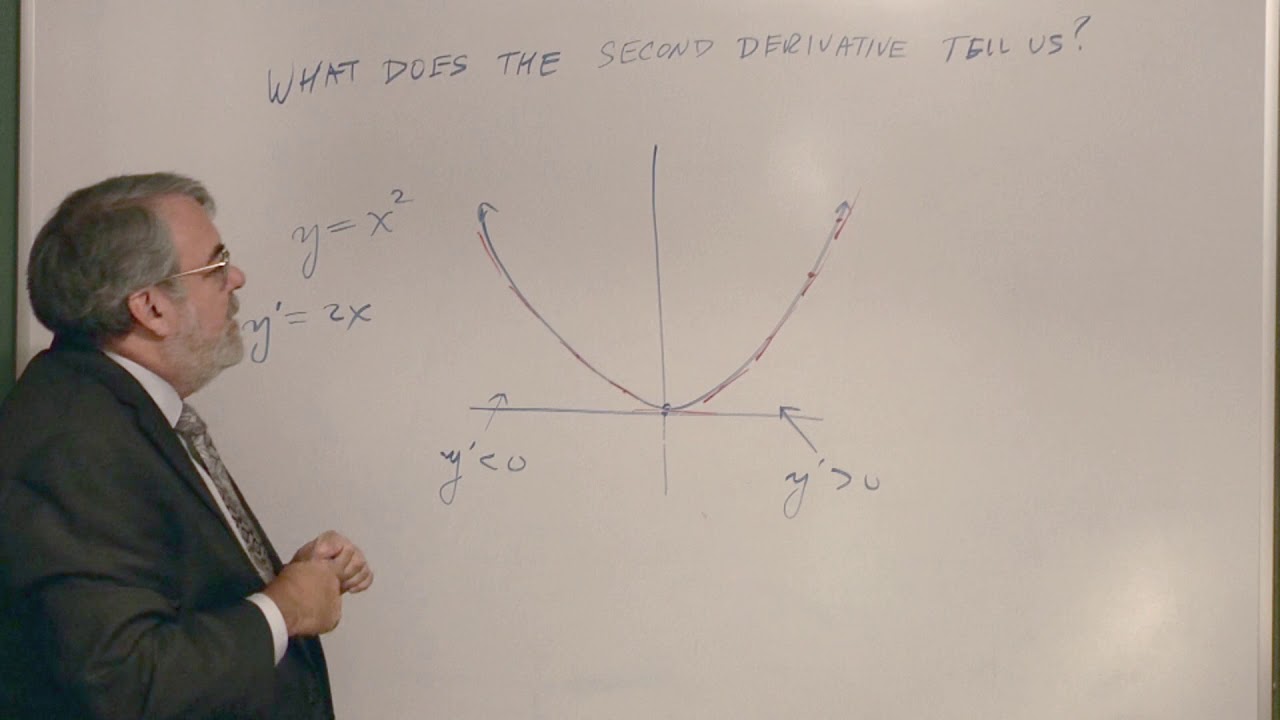
What the Second Derivative Tells Us

Related Tags

Derivatives Slope Analysis Concavity Inflection Points Mathematics Function Graphing Calculus Critical Points Educational Content Learning Materials Math Tutorial