Second derivative test | Application of Derivative | | Class 12
TLDRThe video script delves into the concept of the second derivative test for identifying local maxima, minima, and points of inflection in functions. It builds on the first derivative test, explaining why the second derivative test is essential. The script methodically breaks down the steps to identify critical points and determine their nature using the second derivative. Through examples and problem-solving, it clarifies the conditions under which these points occur, emphasizing the conceptual understanding needed to apply these methods effectively.
Takeaways
- 📚 Derivative tests help in determining local maxima and minima of functions.
- 🧠 The first derivative test identifies critical points where local maxima or minima might occur.
- 🔍 The second derivative test is used to confirm whether a critical point is a local maximum, minimum, or a point of inflection.
- 🔄 Sign changes in the first derivative around critical points indicate whether the function is increasing or decreasing.
- ➕ A positive second derivative at a critical point indicates a local minimum.
- ➖ A negative second derivative at a critical point indicates a local maximum.
- 🔄 If the second derivative changes sign, the point is a point of inflection.
- 📝 To find critical points, set the first derivative equal to zero and solve for the variable.
- 🔎 Checking the second derivative at these points helps determine the nature (maxima, minima, or inflection).
- 💡 The process involves calculating derivatives, evaluating signs, and interpreting results to understand the function's behavior.
Q & A
What is the main topic discussed in the provided transcript?
-The main topic discussed in the transcript is the use of the second derivative test to determine local maxima and minima in a function.
Why is the second derivative test necessary if the first derivative test is already available?
-The second derivative test is necessary because it provides additional insight into the concavity of the function, which helps confirm whether a critical point is a local maximum, local minimum, or a point of inflection.
What is the first step in using the second derivative test to find local maxima or minima?
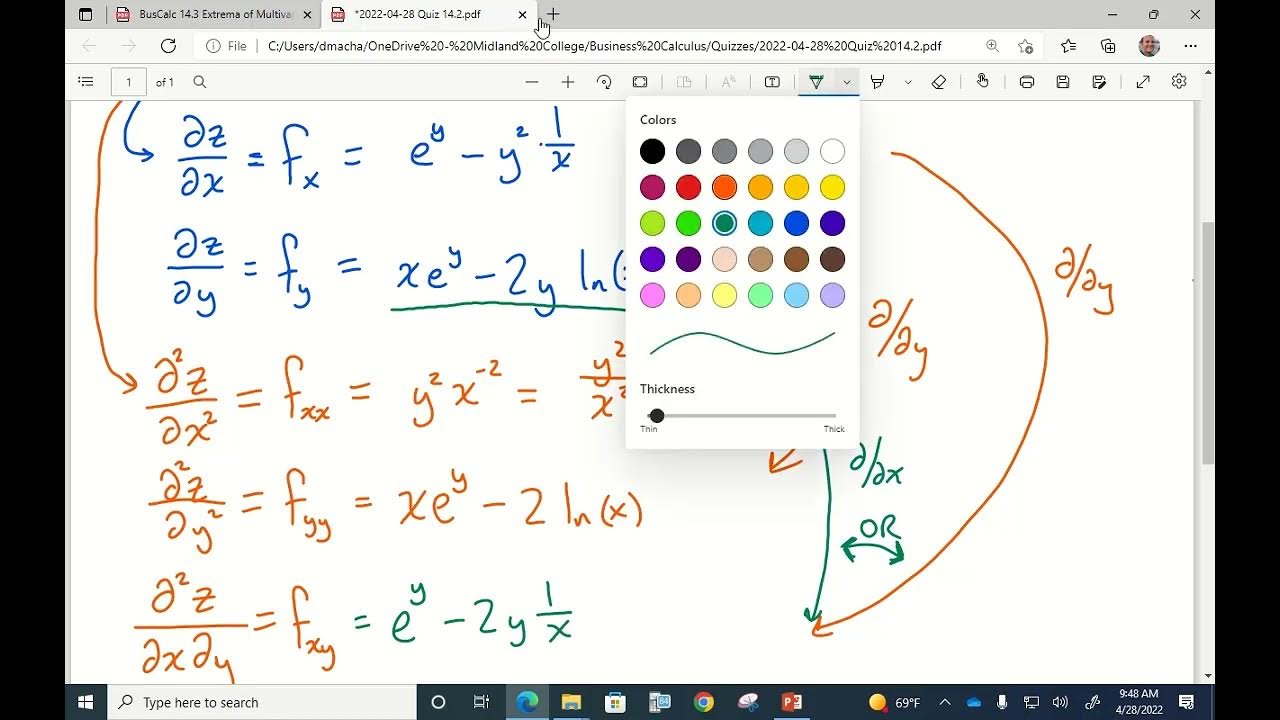
-The first step is to find the first derivative of the function, set it equal to zero, and solve for the critical points.
How do you determine if a critical point is a local maximum, local minimum, or a point of inflection using the second derivative?
-You evaluate the second derivative at each critical point. If the second derivative is positive, the point is a local minimum. If it is negative, the point is a local maximum. If the second derivative is zero, the test is inconclusive, and further analysis is needed.
What does it mean when the second derivative at a critical point is zero?
-When the second derivative at a critical point is zero, it means that the test is inconclusive, and the point could be a point of inflection, local maximum, or local minimum. Additional tests, such as higher-order derivatives, may be required.
Can the second derivative test be used to determine points of inflection?
-Yes, the second derivative test can help identify points of inflection. A point where the second derivative changes sign indicates a point of inflection.
How do you handle a situation where the second derivative test fails to determine the nature of a critical point?
-If the second derivative test fails (i.e., the second derivative is zero), you may need to use the third or higher-order derivatives to determine the nature of the critical point.
What is the significance of the sign of the second derivative in determining local extrema?
-The sign of the second derivative indicates the concavity of the function at a critical point. A positive second derivative indicates concavity upwards (local minimum), while a negative second derivative indicates concavity downwards (local maximum).
What is the relationship between the function's first derivative and its behavior at a critical point?
-At a critical point, the first derivative of the function is zero, which indicates that the function has a horizontal tangent line at that point. This is necessary for a point to be a local maximum, minimum, or point of inflection.
How can you generalize the second derivative test for higher-order derivatives?
-If the second derivative test is inconclusive, you can generalize the approach by examining higher-order derivatives. If the nth derivative is the first non-zero derivative at a critical point, the nature of the point can be determined: if n is even, the point is a local extremum (minimum if positive, maximum if negative); if n is odd, the point is a point of inflection.
Outlines
📚 Introduction to Derivative Tests
The paragraph introduces the concept of derivative tests used in calculus to find local maxima and minima of a function. It discusses the first derivative test and the second derivative test, explaining why the second derivative is helpful in determining the nature of critical points. The speaker uses an example to illustrate the process of finding critical points and mentions the importance of understanding the concepts behind these tests.
🔍 Analyzing the Second Derivative Test
This paragraph delves deeper into the second derivative test, exploring its application in identifying local maxima and minima. It discusses how changes in the sign of the second derivative can indicate the type of critical point—whether it's a maximum, minimum, or point of inflection. The speaker also provides an example function and explains the steps to apply the second derivative test to determine the nature of its critical points.
📉 Understanding the Concept of Function Behavior
The speaker discusses the behavior of functions, particularly focusing on how to interpret the changes in the function's values and slopes. They mention the importance of understanding the concepts of increasing and decreasing functions and how these relate to the derivative tests. The paragraph also touches on the idea of 'subscription' in the context of function analysis, although it's unclear how this relates to the mathematical concepts being discussed.
📈 Advanced Derivative Test Applications
This paragraph presents a more complex application of derivative tests, including the use of higher-order derivatives. It discusses scenarios where the function's behavior is not straightforward and requires a deeper analysis. The speaker provides a detailed example, including calculations and interpretations of the results, to demonstrate how to handle more complicated functions using derivative tests.
🤔 Reflecting on the Learning Process
The speaker reflects on the learning process of derivative tests, emphasizing the importance of understanding the underlying concepts rather than just memorizing formulas. They encourage the audience to engage with the material and practice applying the tests to various functions. The paragraph ends with a reminder to stay engaged and to continue learning in the upcoming classes.
📝 Conclusion and Future Learning
In the concluding paragraph, the speaker summarizes the key points covered in the video script about derivative tests. They mention the importance of recognizing absolute maximum and minimum points within a total range and encourage the audience to continue their studies for the next class. The speaker also hints at the complexity of the subject and the need for ongoing learning and practice.
Mindmap
Keywords
💡Derivative Test
💡Local Maximum
💡Local Minimum
💡First Derivative Test
💡Second Derivative Test
💡Critical Point
💡Inflection Point
💡Concavity
💡Function Behavior
💡Sign Change
Highlights
Understanding the secondary derivative test for finding local maxima and minima in functions.
The importance of sign conventions in determining local maxima and minima.
Using the first derivative test to identify potential critical points.
Explanation of the secondary derivative test to confirm the nature of critical points.
Detailed step-by-step method for applying the secondary derivative test.
Examples of using the second derivative to determine if a critical point is a maximum or minimum.
The significance of positive and negative signs in derivatives.
Explanation of the conditions under which a point can be classified as a point of inflection.
The relationship between increasing and decreasing functions and their derivatives.
Using higher-order derivatives to further analyze the nature of critical points.
Generalizing the method to apply to functions with higher degrees.
Practical examples illustrating the application of the secondary derivative test.
Graphical representation of functions to understand the concepts better.
Detailed problem-solving approach to reinforce the learning.
Summary and review of the concepts covered in the lesson.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: