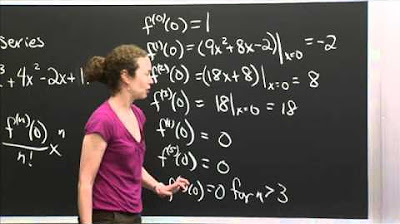Padé Approximants

Dr. Will Wood
14 Aug 202106:48
EducationalLearning
32 Likes 10 Comments

TLDRThis script explores the use of Padé approximants as a method to approximate functions with rational polynomials, offering an alternative to Taylor series. It explains that Padé approximants, represented as a ratio of two polynomials, can provide a more accurate and stable approximation, especially for larger values of x. The video demonstrates the construction of a Padé approximant by matching it to the Taylor series of a function up to a certain order, using sine of x as an example. It shows that Padé approximants can closely follow the original function for a longer range of x due to the division of polynomials, which mitigates the tendency to diverge to infinity, a common issue with Taylor series.

Takeaways
  • 📚 A Padé approximant is a rational polynomial used to approximate functions, consisting of one polynomial divided by another.
  • 🔍 Padé approximants are denoted as P_{m,n} and are formed by an n-th degree polynomial in the numerator and denominator.
  • 📈 Padé approximants can be preferable to Taylor series for certain functions, as they can follow the function more closely for a longer range of values.
  • 🔧 Taylor series use repeated differentiation to produce a polynomial approximation of a function around a specific point, typically x = 0.
  • 📉 One limitation of Taylor series is their tendency to diverge rapidly to infinity for values of x far from the point of expansion.
  • 📝 The construction of a Padé approximant involves matching it to the first m + n terms of the Taylor series of the original function.
  • 📊 A common practice in constructing Padé approximants is to set b_0 = 1 to simplify the algebra involved in finding coefficients.
  • 🧩 By equating the Padé approximant to the Taylor series and solving the resulting system of equations, the coefficients of the approximant can be determined.
  • 📐 The advantage of Padé approximants over Taylor series is their ability to cancel out the tendency to diverge, making them more stable for large x values.
  • 📚 The process of constructing an n over m Padé approximant involves calculating the Taylor series up to order n + m, equating terms, and solving for coefficients.
  • 📘 Padé approximants are particularly useful for functions that oscillate, like sine, where the dominant term in the approximant helps maintain a closer approximation to the actual function as x increases.
Q & A

  • What is a Padé approximant?

    -A Padé approximant is an approximation of a function using rational polynomials, which is one polynomial divided by another. It is formed of an nth degree polynomial in the numerator and an nth degree polynomial in the denominator, and is often written as Pₘₙ.

  • Why might we use Padé approximants instead of Taylor series for function approximation?

    -Padé approximants might be preferred because they often follow the function more closely for a longer range compared to Taylor series, which can diverge rapidly to positive or negative infinity, especially for large values of x.

  • How does a Taylor series provide an approximation of a function?

    -A Taylor series provides an approximation of a function by using repeated differentiation to produce a polynomial approximation about a particular point in x, typically x=0. It sums terms of the form f(n)(0) * x^n / n!, where f(n) denotes the nth derivative of the function.

  • What is the general form of a Taylor series for a function f(x) around x=0?

    -The general form of a Taylor series for a function f(x) around x=0 is f(x) ≈ f(0) + x * f'(0) + x^2 / 2! * f''(0) + ... + x^n / n! * f^(n)(0), where f^(n) denotes the nth derivative of f.

  • Can you provide an example of a Taylor series for a specific function?

    -Sure, for the function f(x) = e^(-x), the Taylor series at x=0 is 1 + x * (-1) + x^2 / 2! * (-1) + higher-order terms, which simplifies to 1 - x + x^2/2 + ... and includes a big O term to represent the error due to omitted terms.

  • What is the main drawback of using Taylor series for function approximation?

    -The main drawback of using Taylor series is that they often cannot extrapolate the function for very long before rapidly diverging to positive or negative infinity, making them less suitable for large values of x.

  • How is a Padé approximant constructed?

    -A Padé approximant is constructed to agree with the first m+n terms of a Taylor series. It involves equating the Padé approximant with the Taylor series and solving a set of linear equations to calculate the coefficients of the polynomials in the numerator and denominator.

  • Why is it common to set b₀ to 1 when constructing a Padé approximant?

    -Setting b₀ to 1 simplifies the algebra involved in constructing the Padé approximant without loss of generality. It helps in solving the linear equations by normalizing the denominator.

  • What is the significance of the x^4 term in the construction of a Padé approximant for sine(x)?

    -In the construction of a Padé approximant for sine(x), the x^4 term is significant because it is part of the Taylor series up to the fourth order, which the Padé approximant must agree with. Even though it is zero, it is included to ensure the correct approximation.

  • How does the Padé approximant compare to the Taylor series in terms of following the original function?

    -The Padé approximant tends to stay closer to the original function for a longer range compared to the Taylor series. This is because the rational polynomial structure of the Padé approximant helps to cancel out the tendency to diverge towards infinity as x increases.

  • What is the general process for constructing an n/m Padé approximant for a given function?

    -To construct an n/m Padé approximant, one first calculates the Taylor series up to order n+m, equates it to the Padé approximant, and then solves a set of simultaneous equations to find the coefficients. It's standard practice to let b₀=1, and the equations are derived by equating terms of like powers of x.

Outlines
00:00
📚 Rational Function Approximations: Pade Approximants

This paragraph introduces Pade approximants as a method of approximating functions using rational polynomials, which are ratios of two polynomials. It contrasts Pade approximants with Taylor series, explaining that while Taylor series can diverge for large values of x, Pade approximants tend to follow the function more closely over a longer range. The construction of a Pade approximant is described, emphasizing the need for it to agree with the first m+n terms of the Taylor series of the function. An example using the sine function is provided, demonstrating how to set up and solve the equations to find the coefficients of the approximant. The summary also notes the inclusion of the 'big O' notation to represent the error term and the significance of the x^4 term being zero in the example.

05:01
🔍 Advantages of Pade Approximants Over Taylor Series

The second paragraph delves into the advantages of Pade approximants over Taylor series, particularly their behavior as x approaches infinity. It explains that while Taylor series can lead to negative infinity due to the dominance of the x^3 term, Pade approximants, with their 1/x^2 dominant term, approach zero, which is preferable for functions like sine that oscillate around zero. The paragraph outlines the steps for constructing an n/m Pade approximant: calculating the Taylor series up to order n+m, equating it to the Pade approximant, and solving the resulting set of simultaneous equations. The process involves multiplying both sides by the denominator, expanding, and ignoring higher-order terms. The paragraph concludes by highlighting that for an n/m Pade approximant, there are n+m equations to solve for n+m unknowns.

Mindmap
Keywords
💡Padé approximant
A Padé approximant is a rational function used to approximate another function, typically constructed as a ratio of two polynomials. In the video, it is described as an 'approximation of a function using rational polynomials,' where one polynomial is divided by another. The script discusses the construction of a Padé approximant and how it can follow a function more closely for a longer range compared to Taylor series.
💡Rational polynomials
Rational polynomials refer to the ratio of two polynomials. In the context of the video, they are the building blocks of a Padé approximant, where one polynomial (numerator) is divided by another (denominator), both of which are of the same degree. The script mentions that a Padé approximant is 'one polynomial divided by another'.
💡Taylor series
The Taylor series is a mathematical representation of a function as an infinite sum of terms calculated from the values of the function's derivatives at a single point. The video script contrasts the Padé approximant with the Taylor series, explaining that while Taylor series uses repeated differentiation, Padé approximants can sometimes offer better approximations over a longer range.
💡Differentiation
Differentiation is a mathematical process to find the derivative of a function, which represents the rate at which the function changes with respect to one of its variables. In the script, differentiation is used in the context of constructing a Taylor series, where the derivatives of a function at a particular point are calculated to form the polynomial approximation.
💡Approximation
Approximation in this context refers to the process of finding a function that closely resembles another function over a certain range. The video discusses the use of Padé approximants and Taylor series as methods for approximating functions, with Padé approximants often providing a more accurate approximation over a longer range.
💡Extrapolation
Extrapolation is the process of estimating values of a function outside the range of known data. The script points out that Taylor series often cannot extrapolate a function for very long before rapidly diverging to infinity, whereas Padé approximants can follow the function more closely for a longer range.
💡Polynomial
A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, and multiplication, and non-negative integer exponents. The video script explains that both the numerator and the denominator of a Padé approximant are polynomials of the same degree.
💡Coefficients
Coefficients are the numerical factors in a term of a polynomial. In the video, the script describes the process of calculating the coefficients of the Padé approximant's polynomials to ensure that the approximant agrees with the Taylor series up to a certain order.
💡Linear equations
Linear equations are algebraic equations in which each term is either a constant or the product of a constant and a single variable. The script explains that after setting up the Padé approximant to match the Taylor series, one ends up with a set of linear equations that can be solved to find the coefficients of the approximant.
💡Simultaneous equations
Simultaneous equations refer to multiple equations that are solved at the same time. In the context of the video, the script describes how equating the terms of the Padé approximant and the Taylor series results in a set of simultaneous equations that must be solved to determine the coefficients of the approximant.
💡Dominant term
The dominant term in a polynomial or a series is the term that has the greatest influence on the behavior of the function, especially as the variable approaches infinity. The script uses the term to explain why the Taylor series diverges to infinity for large values of x, while the Padé approximant approaches zero due to the dominant term being 1/x^2.
Highlights

A Padé approximant is an approximation of a function using rational polynomials.

It consists of one polynomial divided by another, specifically an nth degree polynomial in the numerator and denominator.

Padé approximants are sometimes denoted as P_m^n.

Taylor series uses repeated differentiation to produce a polynomial approximation of a function about a particular point in x.

Taylor series often can't extrapolate the function for very long before rapidly diverging to positive or negative infinity.

Padé approximants often follow the function more closely for a longer range.

The construction of a Padé approximant involves agreeing with the first m+n terms of a Taylor series.

For a 2/2 Padé approximant of sine(x), it must agree with the fourth order Taylor series of sine(x).

It's common practice to let b0 equal one to simplify the algebra involved in constructing a Padé approximant.

By multiplying both sides by the denominator and ignoring terms higher than the degree of the original Taylor series, we can solve for the coefficients.

The resulting Padé approximant for sine(x) is x/(1 + x^2/6).

Padé approximants stay closer to the original function for a longer range compared to Taylor series.

As x tends to infinity, Taylor series tends to minus infinity, while Padé approximants approach 0, which is better for functions like sine(x).

Dividing one polynomial by another in a Padé approximant cancels out the tendency to shoot towards plus or minus infinity.

To construct an n/m Padé approximant, calculate the Taylor series up to order n+m, equate it to the Padé approximant, and solve the resulting equations.

For an n/m Padé approximant, there will be n+m equations and n+m unknowns to solve.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 10.11 Part 1

Taylor Polynomials

Avon High School - AP Calculus BC - Topic 10.11 - Example 2

Finding Taylor Series

Taylor's Series of a Polynomial | MIT 18.01SC Single Variable Calculus, Fall 2010

Taylor Polynomials Day 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Padé ApproximantFunction ApproximationTaylor SeriesRational PolynomialsMathematicsNumerical AnalysisSeries ExpansionAlgebraic TechniquesError AnalysisPolynomial Division