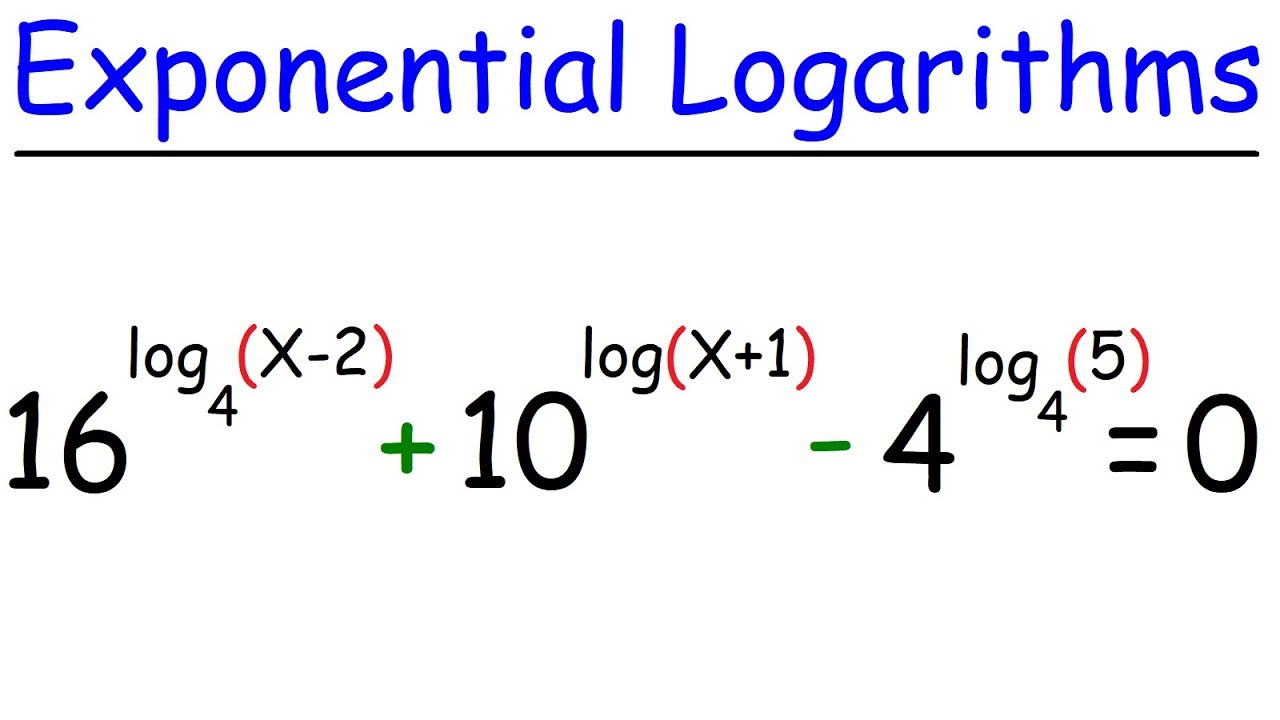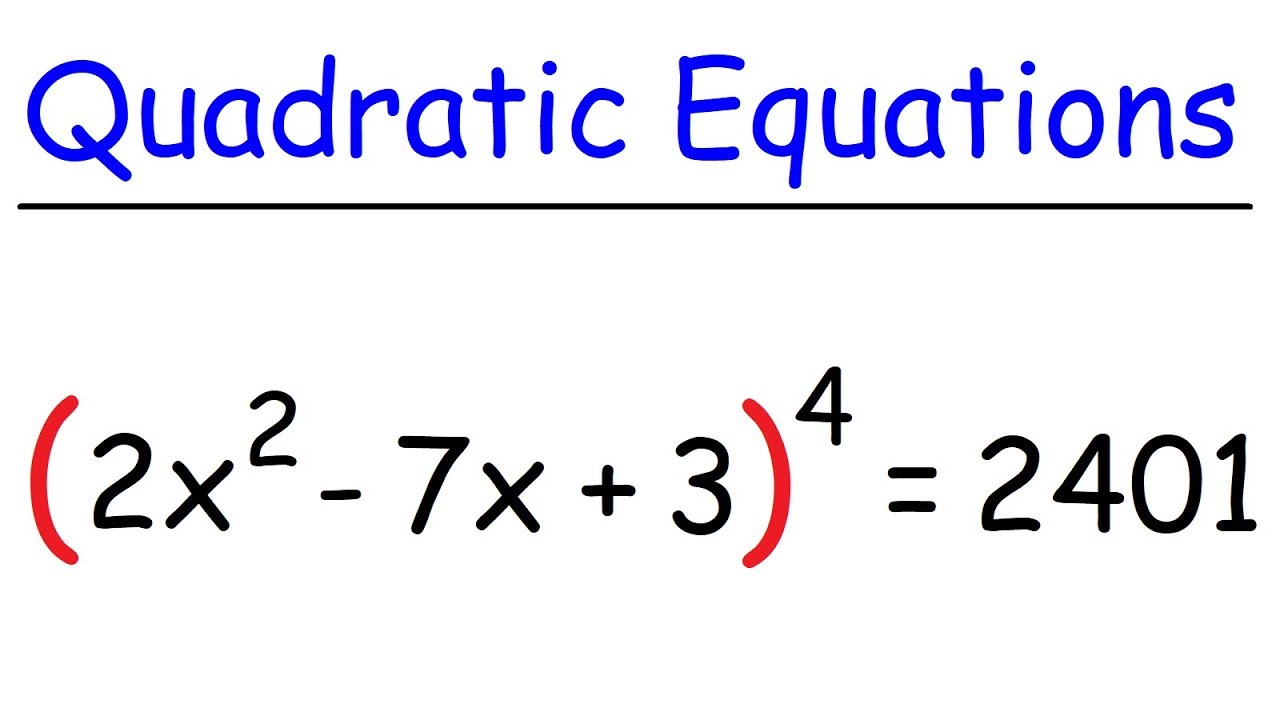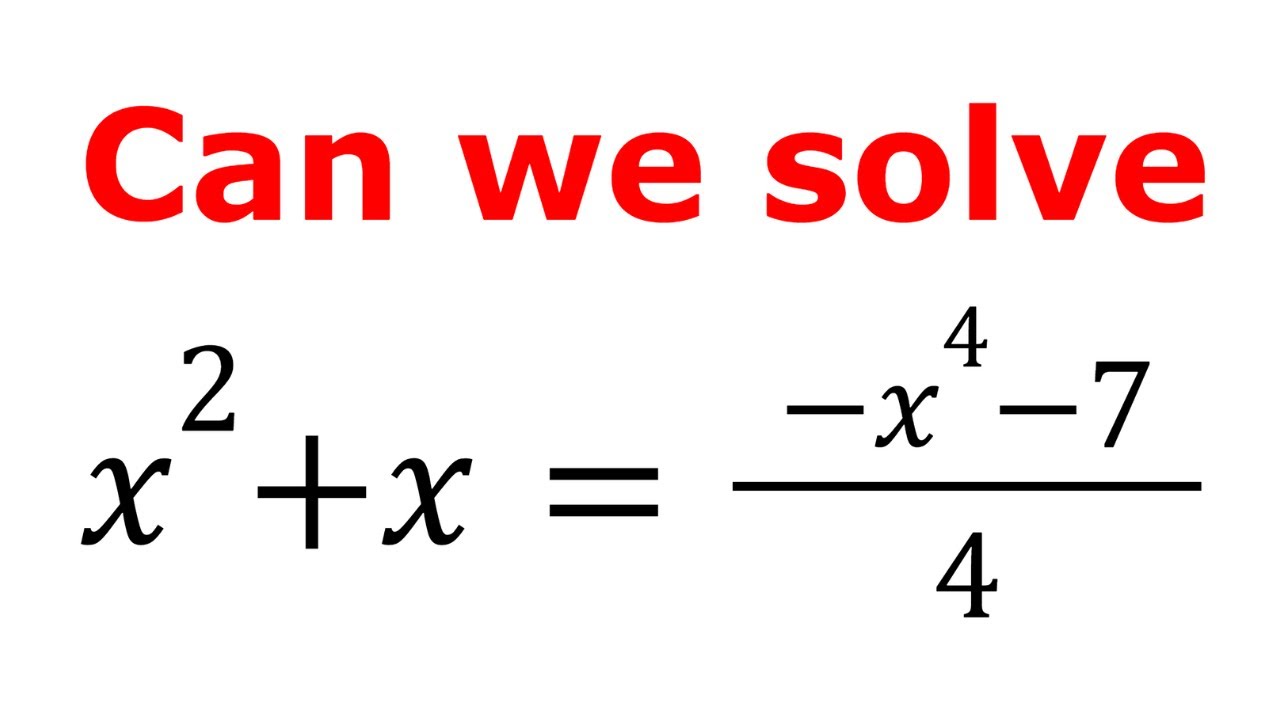Can We Solve A Nice Factorial Equation

SyberMath

1 Mar 202409:31

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, the presenter tackles a unique factorial equation: x factorial equals x cubed minus x. The video begins with a graphical representation of both x factorial and x cubed minus x, highlighting their intersection between one and two. The presenter then systematically solves the equation, excluding non-integer solutions and zero or one as potential solutions. Through factoring, cancellation, and substitution, the presenter narrows down the possible integer solutions. After testing various values, the video concludes that x equals five is the only integer solution that satisfies the original equation, providing a clear demonstration of mathematical problem-solving.

Takeaways

📊 The video aims to solve a factorial equation: X! = X³ - X, focusing on integer solutions.
📉 Graphs of X factorial (a discrete function) and X³ - X are shown to illustrate intersections between the curves.
🔢 X factorial can be extended to real numbers using the gamma function.
🔍 Wolfram Alpha provides two numerical solutions that are not integers, prompting the need to solve for integer solutions.
📝 X factorial is expressed as X * (X - 1)!, and X³ - X is factored as X * (X² - 1).
⚠️ Zero and one are not valid solutions since they lead to inconsistencies in the original equation.
🔄 Substitution is used to simplify the equation, letting Y = X - 2, leading to the equation Y! = Y + 3.
🧮 Solving Y! = Y + 3 by checking potential integer values, leading to possible X values of 3, 1, and 5.
❌ X = 3 and X = 1 do not satisfy the equation upon verification.
✅ X = 5 is the correct integer solution, where 5! equals 5³ - 5, confirming the solution.

Q & A

What is the equation being solved in the video?
-The equation being solved is x factorial = x^3 - x.
What is the significance of the graph in the video?
-The graph is used to visualize the intersection points between x factorial and x^3 - x, which helps in understanding where the solutions might lie.
Why is the gamma function mentioned in the video?
-The gamma function is mentioned because it allows the definition of factorial for all real numbers, not just non-negative integers.
What are the limitations of the equation when considering x = 0?
-The equation is not defined for x = 0 in the context of integers because 0 factorial is not defined, but it can be defined within the real numbers.
Why is x = 1 not a solution to the equation?
-x = 1 is not a solution because 1 factorial equals 1, and 1^3 - 1 equals 0, which does not satisfy the equation.
What is the process of simplifying the equation after canceling out x?
-After canceling out x, the equation is simplified by expanding x factorial as x * (x - 1) factorial and x^3 - x as x * (x^2 - 1), and then using the difference of squares to further simplify.
What substitution is made to simplify the problem?
-The substitution made is to let y = x - 2, which simplifies the equation to y factorial = y + 3.
Why is it stated that factorials grow much faster than linear functions?
-Factorials grow exponentially, meaning they increase much more rapidly than linear functions, which makes it easier to find the turning point where the factorial overtakes the linear function.
How are the potential solutions for y determined?
-The potential solutions for y are determined by the fact that either y or (y - 1) factorial minus one must be a factor of three, leading to possible values of y being 1, 3, or -3.
What is the final integer solution found for x in the video?
-The final integer solution found for x is 5, as 5 factorial equals 120 and 5^3 - 5 equals 120, satisfying the original equation.

Outlines

00:00

🔢 Solving a Factorial Equation: Introduction and Graphs

In this video, we tackle a factorial equation: \(x!\) (factorial) equals \(x^3 - x\). Initially, we visualize the graphs of \(x!\) and \(x^3 - x\), noting that \(x!\) is typically defined for non-negative integers, but can be extended to real numbers using the Gamma function. The graphs suggest intersections between 1 and 2, prompting us to solve for integer solutions. Despite solutions from Wolfram Alpha being non-integer, we aim to find integer solutions through factorization and simplification.

05:03

🧩 Factorizing and Simplifying the Equation

We start by factorizing both sides of the equation: \(x! = x(x - 1)!\) and \(x^3 - x = x(x^2 - 1)\). After ruling out \(x = 0\) and \(x = 1\) as solutions due to undefined or incorrect results, we proceed by canceling out common factors and further factorizing. The goal is to simplify the equation to identify valid integer solutions. This involves breaking down \( (x - 1)! \) further and using the difference of squares method.

🔄 Substitution and Systematic Solution Approach

Introducing a substitution, we let \(y = x - 2\), transforming the equation to \( y! = y + 3 \). This simplification helps in solving the equation more systematically. We explore different values of \(y\) and their corresponding \(x\) values, determining which satisfy the equation. This step involves checking each value to see if it meets the criteria for valid solutions.

✅ Validating Solutions and Conclusion

After substituting and testing various values, we identify \(x = 5\) as a valid solution where \(5! = 120\) and \(5^3 - 5 = 125 - 5 = 120\). We conclude that \(x = 5\) is the only integer solution. The video wraps up with a confirmation of the solution, an invitation to comment, like, and subscribe, and a sign-off message for viewers.

Mindmap

Keywords

💡Factorial

A factorial, denoted by an exclamation mark (!), is a mathematical function that multiplies a sequence of descending natural numbers. For example, 5! equals 5 * 4 * 3 * 2 * 1. In the video, the speaker discusses 'x factorial' as a function that can be extended to real numbers using the gamma function, and it is central to solving the given equation.

💡Graph

A graph in mathematics is a visual representation of data points, showing the relationship between variables. In the context of the video, the speaker mentions the graph of 'x factorial' and 'x cub - x' to illustrate the intersection points, which is crucial for understanding where the solutions might lie.

💡Gamma Function

The gamma function is a mathematical extension of the factorial function to complex numbers, defined for all complex numbers except the negative integers. In the video, it is mentioned as a way to define factorial for all real numbers, which is essential for graphing 'x factorial'.

💡Intersection

In the context of graphs, an intersection refers to the point where two graphs meet. The video script discusses the intersection of 'x factorial' and 'x cub - x' as a key visual clue to finding the solution to the equation.

💡Factor

To factor in mathematics means to express a polynomial as the product of its factors. In the video, the speaker factors 'x cub - x' into 'x * x^2 - 1' and uses this to simplify the equation and find a solution.

💡Difference of Squares

The difference of squares is a factoring technique where a^2 - b^2 equals (a + b)(a - b). The video script uses this technique to factor 'x^2 - 1' into '(x + 1)(x - 1)', which simplifies the equation-solving process.

💡Substitution

Substitution is a method used in algebra where one expression is replaced with another for simplification. The speaker introduces 'y' as a substitution for 'x - 2' to simplify the equation and make it easier to solve.

💡Turning Point

A turning point in the context of graphs refers to a point where the graph changes direction. The video mentions that factorials grow faster than linear functions, implying that the turning point will be reached quickly, which helps in narrowing down the solution.

💡Divide

In mathematics, dividing is the process of partitioning a number into equal parts. The video script discusses dividing both sides of the equation by 'x' after establishing that 'x' cannot be zero, which is a crucial step in solving the equation.

💡Integer Solutions

Integer solutions are solutions that are whole numbers. The video's main goal is to find integer values of 'x' that satisfy the equation 'x factorial = x cub - x', which is the central theme of the video.

💡Solve

To solve in mathematics means to find the answer to a problem or equation. The entire video is focused on solving the given factorial equation for integer values of 'x', which is the main objective of the content.

Highlights

The video aims to solve a factorial equation where x factorial equals x cubed minus x.

A graph is shown comparing x factorial and x cubed minus x, suggesting an intersection between 1 and 2.

The gamma function allows defining factorial for all real numbers, not just non-negative integers.

W|A from Alpha suggests two numerical solutions which are not integers.

The equation is solved for integers, not real numbers, as the factorial is defined for non-negative integers.

Factoring both sides of the equation simplifies the problem.

The video explains why x cannot be 0 or 1 based on the definition of factorial.

The equation simplifies to x - 2 factorial equals x + 1 after canceling out x.

Substitution of y for x - 2 simplifies the equation to y factorial equals y + 3.

A systematic approach is used to find integer solutions for y.

The turning point of the factorial function is discussed in relation to linear functions.

The equation y factorial minus y equals 3 is derived and factored.

The factors of 3 are considered to find possible values for y.

The video tests the possible values of y to find corresponding x values.

Only x equals 5 is found to satisfy the original equation after testing.

The video concludes that x equals 5 is the solution to the equation.

Transcripts

Browse More Related Video

An Interesting Olympiad Problem With Factorials

Let's Solve A Nice Factorial Equation

Exponential Logarithmic Equations

Exponential Equations With Powers of X

Solving Quadratic Equations With Exponents

Solving A Quartic | Two Methods