Solving A Quartic | Two Methods

SyberMath
5 Mar 202412:30
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter tackles a quartic equation, transforming it into a full quartic by cross-multiplying. Recognizing it as a depressed quartic due to the absence of an x^3 term, they introduce two methods for solving it. The first approach involves using the quartic formula, simplifying it to a cubic equation for 'a' and 'b'. The second method cleverly restructures the equation as a difference of squares, leading to a system of equations with integer solutions for 'a', 'b', and 'c'. The presenter solves for these variables, revealing the factored form of the original equation and applying the quadratic formula to find all solutions. The video concludes with an invitation for viewers to engage, like, and subscribe for more content.

Takeaways
  • 📚 The video is about solving a quartic equation, specifically a depressed quartic, which lacks an \( x^3 \) term.
  • 🔍 The presenter starts by transforming the given equation into a full quartic by cross-multiplying and rearranging terms.
  • 📝 The equation is \( x^4 + 4x^2 + 4x + 7 = 0 \), which is then factored in an attempt to solve it using the quartic formula.
  • 🧐 The presenter discusses the possibility of using perfect squares to simplify the equation but opts for a different method.
  • 📈 A system of equations is derived to find the values of \( a \) and \( b \) that will help factor the quartic equation.
  • 🔢 The presenter simplifies the system to a cubic equation in terms of \( b \) and attempts to solve for \( a \) and \( b \).
  • 🎯 The second method involves rewriting the quartic equation as a difference of two squares, aiming to find integer solutions.
  • 🔍 The presenter sets up a system of equations to find integer values for \( a \), \( b \), and \( c \) that satisfy the equation.
  • 📉 The rational root theorem is used to test for possible integer values of \( a \), leading to the discovery that \( a = 3 \) is a solution.
  • 📌 With \( a = 3 \), the presenter finds corresponding values for \( b \) and \( c \), which are \( b = 2 \) and \( c = 1 \) respectively.
  • 📝 The final factored form of the equation is derived, leading to the application of the quadratic formula for the roots.
Q & A

  • What type of equation is being discussed in the video?

    -The video discusses a quartic equation, which is a polynomial of degree four, and it is noted to be a depressed quartic because it lacks an x^3 term.

  • Why is the equation referred to as a 'depressed quartic'?

    -The equation is called a 'depressed quartic' because it does not have an x^3 term, which is typically present in a standard quartic equation.

  • What is the first method presented for solving the quartic equation?

    -The first method presented involves using the quartic formula and rewriting the equation in a factored form to eliminate the x^3 term and solve for the variables a and b.

  • What is the second method for solving the quartic equation mentioned in the video?

    -The second method involves rewriting the equation as a difference of two squares, which introduces three variables (a, b, and c) and aims to find integer solutions for these variables.

  • How does the video suggest simplifying the equation to solve for the variables?

    -The video suggests simplifying by setting up a system of equations based on the coefficients of the terms in the equation and solving for the variables a, b, and c.

  • What is the significance of the constant term '7' in the quartic equation?

    -The constant term '7' is significant as it is formed by the product of b and the constant c, and it is used to set up the equations to solve for the variables.

  • What is the role of the variables a, b, and c in the factored form of the equation?

    -In the factored form, a, b, and c are used to represent the coefficients and constants that, when solved, will help factor the quartic equation into a product of two quadratic equations.

  • How does the video suggest finding the values of a, b, and c?

    -The video suggests using the rational root theorem to test for integer solutions for a, and then using the relationships between a, b, and c to find their respective values.

  • What is the final form of the factored quartic equation according to the video?

    -The final factored form of the equation is (x^2 + 3^2 - 2x - 1^2) = 0, which simplifies to (x + 3 ± √2)(x - 1 ± √2) = 0.

  • What is the conclusion of the video regarding the solutions to the quartic equation?

    -The conclusion is that the solutions to the quartic equation are found using the quadratic formula on the factored quadratic expressions, resulting in four solutions.

Outlines
00:00
📚 Introduction to Solving a Quartic Equation

The video begins with an introduction to solving a quartic equation, which is differentiated from a rational equation due to the absence of variables in the denominator. The presenter outlines the process of transforming the given equation, 4x^2 + 4x = X to 4 - 7, into a full quartic equation by cross-multiplying and moving terms to one side to set the equation to zero. It is noted that the equation is actually a depressed quartic, missing an x^3 term. The presenter then introduces two methods for solving the equation, starting with using the quartic formula and setting up the equation in a factored form to eliminate the x^3 term by manipulating the coefficients a and b.

05:01
🔍 Detailed Analysis Using Quartic Formula

In this paragraph, the presenter delves into the intricacies of using the quartic formula to solve the equation. They set up the equation in a form that allows for the elimination of the x^3 term by introducing variables a and b, which represent the coefficients in the factored form of the equation. The presenter then expands this factored form and compares coefficients to the original equation to derive a system of equations involving a and b. The goal is to isolate these variables and solve for them, which involves algebraic manipulation and potentially solving a cubic equation. The presenter also discusses the possibility of not obtaining integer solutions and the complexity that may arise from that.

10:03
🎯 Alternative Method: Factoring as a Difference of Squares

The presenter introduces an alternative method for solving the quartic equation by rewriting it as a difference of squares. This involves introducing additional variables, a, b, and c, to represent the coefficients in the new form of the equation. The presenter sets up the equation to be factored into (x^2 + ax + a^2) - (bx + c^2) = 0, aiming to simplify the equation into a form that can be solved by finding integer values for a, b, and c. The presenter then solves a system of equations derived from setting the coefficients of like terms equal to each other, eventually finding that a = 3, b = 2, and c = 1. This leads to a factored form of the equation that can be further simplified using the quadratic formula to find the roots of the equation.

🏁 Conclusion and Final Solutions

In the final paragraph, the presenter concludes the video by summarizing the solutions obtained from the alternative method. They rewrite the equation in its factored form using the values of a, b, and c that were determined to be 3, 2, and 1, respectively. The presenter then shows how to factor the equation as a difference of two squares, leading to a quadratic equation that can be solved using the quadratic formula. The presenter provides the roots of the equation and thanks the viewers for watching, encouraging them to comment, like, and subscribe for more content.

Mindmap
Keywords
💡Quartic Equation
A quartic equation is a polynomial equation of degree four, which means the highest power of the variable (x in this case) is four. In the video, the main theme revolves around solving a specific quartic equation, which is initially presented as 4x^2 + 4x = X^4 - 7. The process of solving this equation forms the core of the educational content.
💡Cross Multiplying
Cross multiplying is a mathematical technique used to solve equations, particularly those set as fractions or proportions. In the script, the presenter mentions cross multiplying as a preliminary step to transform the given equation into a 'full quartic' form, which is essential for applying the subsequent solution methods.
💡Depressed Quartic
A depressed quartic is a quartic equation that has been manipulated to lack the x^3 term, making it easier to solve. The script refers to the given equation as a depressed quartic because after the cross multiplication, the x^3 term is missing, which simplifies the solving process.
💡Quartic Formula
While there is no universal 'quartic formula' like the quadratic formula, the term in the script refers to a method or set of methods used to solve quartic equations. The presenter discusses using a quartic formula as one of the methods to approach solving the given equation, indicating a higher-level algebraic technique.
💡Factored Form
Factored form in algebra is when a polynomial is expressed as a product of its factors. The video script mentions rewriting the equation in factored form as a step towards solving it, which is a common strategy for breaking down complex equations into simpler, solvable parts.
💡Perfect Squares
Perfect squares are expressions that can be written as the square of a binomial. In the script, the presenter suggests using perfect squares as a method to transform the equation, which involves manipulating terms to create expressions that are squares of binomials, facilitating the factoring process.
💡Difference of Squares
The difference of squares is a factoring technique where an expression of the form a^2 - b^2 can be factored into (a + b)(a - b). The video script describes using this technique to rewrite the quartic equation as a difference of two squares, which is a key step in the second method presented for solving the equation.
💡Rational Root Theorem
The rational root theorem is a principle in algebra that helps in identifying potential rational roots of a polynomial equation. In the video, the presenter uses the rational root theorem to test for integer solutions for the equation derived from the factoring process, which is a practical approach to finding exact solutions.
💡Quadratic Formula
The quadratic formula is used to solve quadratic equations of the form ax^2 + bx + c = 0. In the script, the presenter mentions using a 'very radical expression' similar to the quadratic formula to find the roots of the equation once it has been reduced to a quadratic form through the factoring process.
💡Coefficient
In algebra, the coefficient is the numerical factor of a term in a polynomial. The video script discusses comparing coefficients of like terms in the equation to those in the factored form, which is a crucial step in matching the original equation to its factored counterpart and solving for the unknowns.
Highlights

The video presents a method to solve a quartic equation without a variable in the denominator.

The equation is transformed into a full quartic by cross-multiplying and then into a depressed quartic.

Two methods are introduced to solve the equation: using the quartic formula and another special method.

The quartic formula method involves factoring the equation and solving for variables a and B.

The video demonstrates how to distribute and simplify the equation to compare coefficients.

A system of equations is formed to solve for the variables, which may result in a cubic equation.

The second method involves writing the equation as a difference of two squares and looking for integer solutions.

Integer values for a, b, and c are sought to simplify the equation into a factored form.

The rational root theorem is used to test for integer solutions, with factors of 12 being tested.

The value of a is found to be 3, which leads to determining the values of b and c.

The final factored form of the equation is derived using the found values of a, b, and c.

The difference of two squares is factored to find the solutions to the quartic equation.

The quadratic formula is applied to find the remaining two solutions of the quartic equation.

The video concludes with the complete solutions to the quartic equation and a thank you message.

The presenter encourages interaction by asking viewers to comment, like, and subscribe.

The video provides a comprehensive guide to solving quartic equations with a focus on practical application.

The method presented avoids complex guessing and checking, offering a structured approach to solving quartic equations.

The use of the rational root theorem is highlighted as a key step in finding integer solutions.

Transcripts

Browse More Related Video

Solving Polynomial Equations By Factoring and Using Synthetic Division

EXTREME quintic equation! (very tiring)

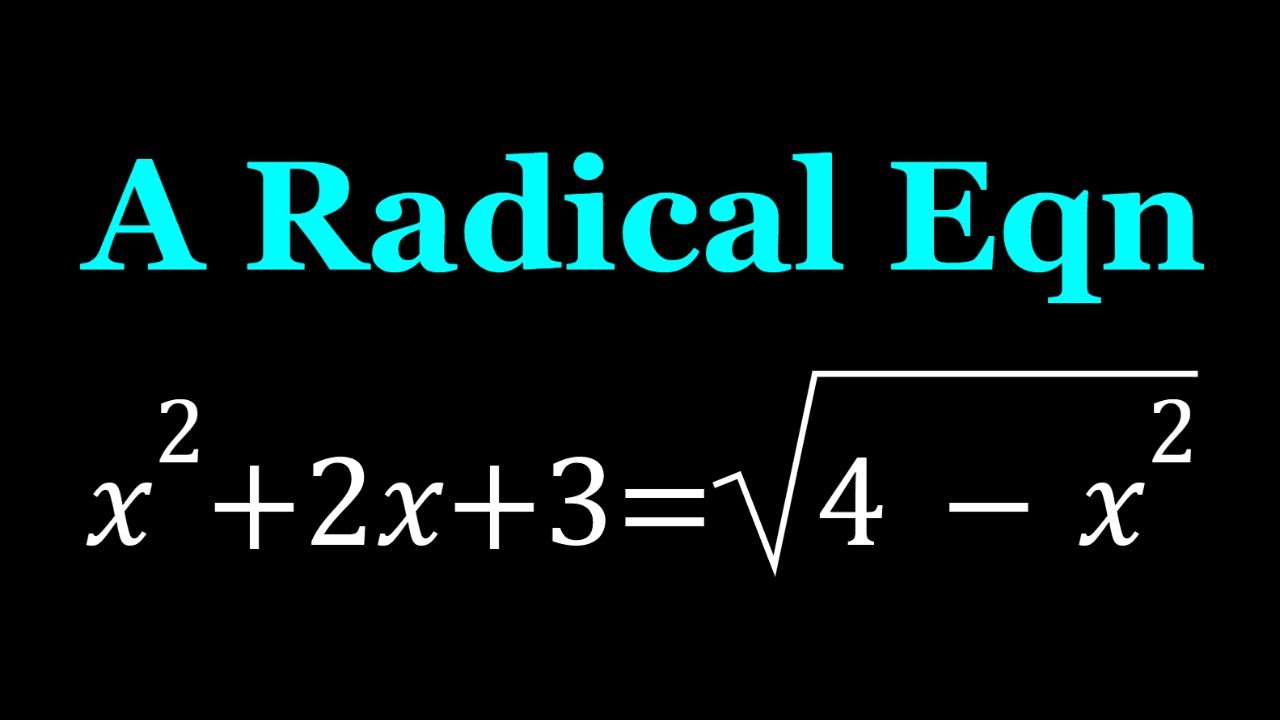
A Cool Radical Equation | Math Olympiads

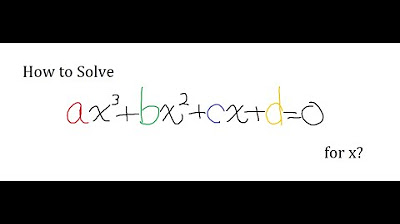
[Algebra] Is there any cubic formula?

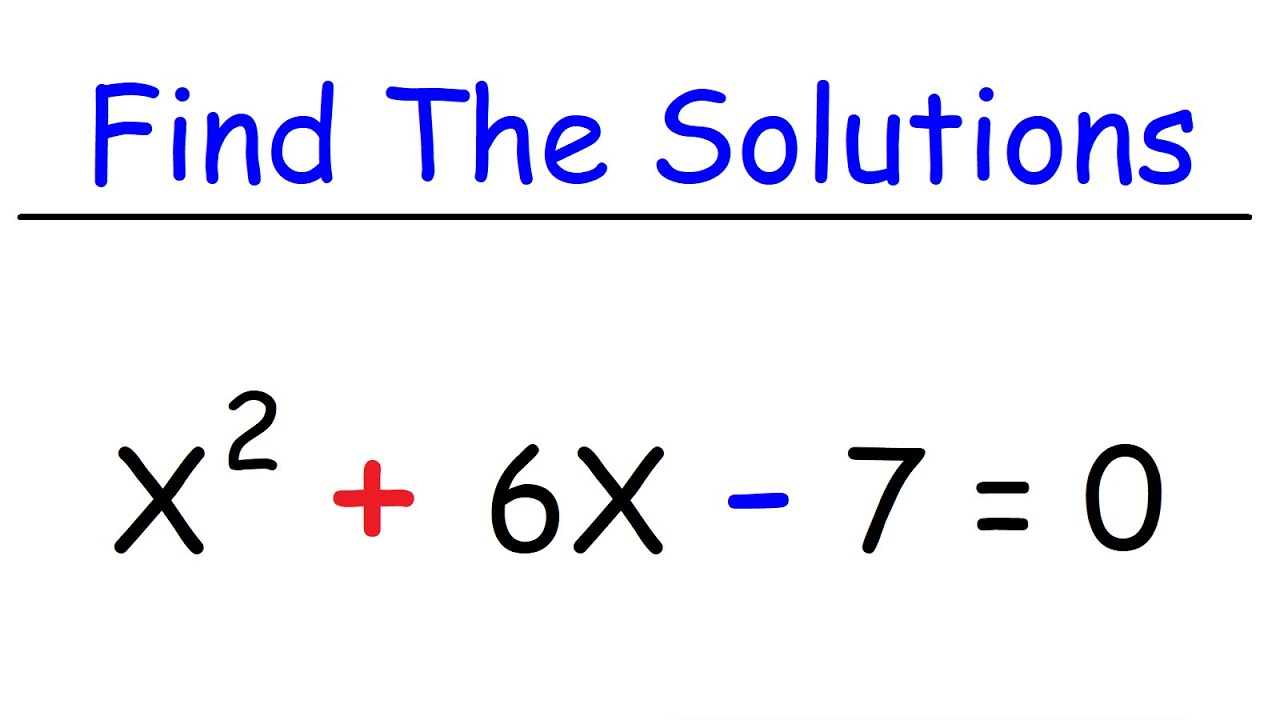
How To Find The Real & Imaginary Solutions of Polynomial Equations

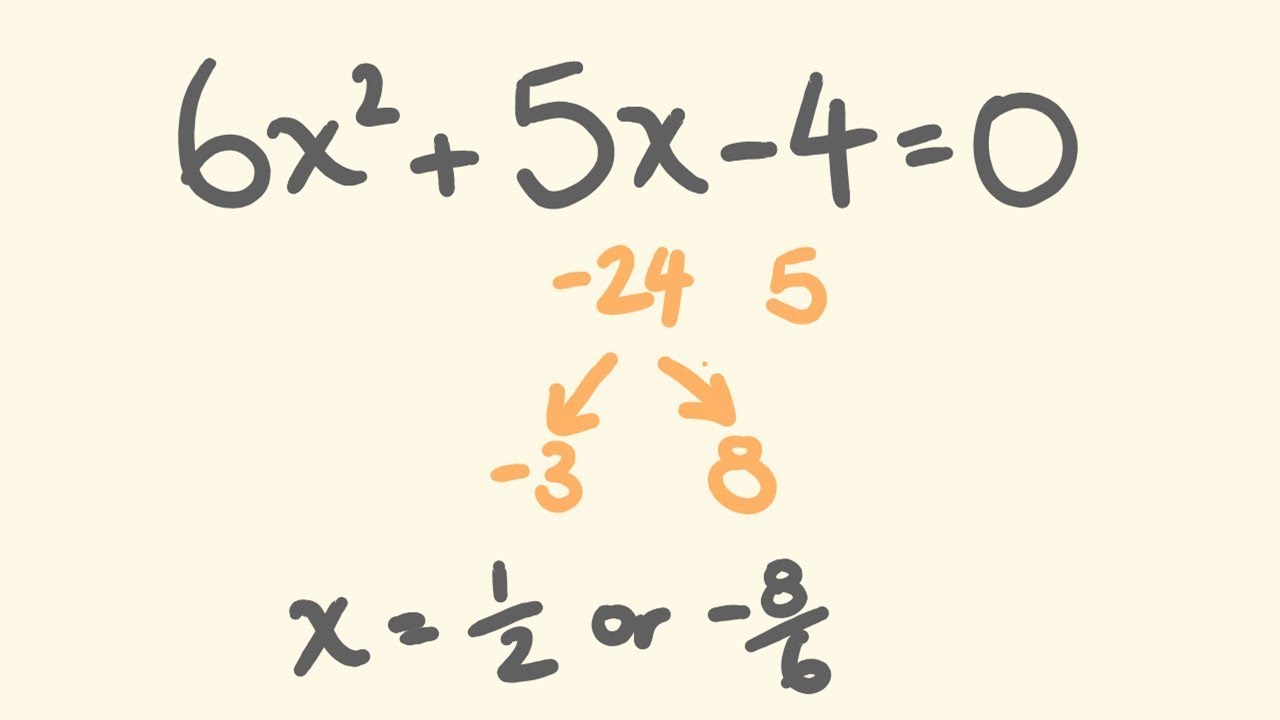
How to Factor any Quadratic Equation Easily - Trick for factorising

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quartic EquationsMathematicsEducationalFactoringQuartic FormulaSolving EquationsAlgebraMath TutorialRootsCoefficients