Let's Solve A Nice Factorial Equation
TLDRIn this video, the presenter tackles a factorial equation, n! + (n - 2)! = n^3 + 1, aiming to find integer solutions for n. Initially, using the gamma function for real numbers, only a non-integer solution is found. However, the focus shifts to integer solutions. By factoring out (n - 2)! from both terms on the left side of the equation, the presenter simplifies the equation and then uses the sum of cubes factorization to further refine the problem. After considering the possibility of the common factor being zero and substituting n - 2 with k, the presenter finds that k = 3 is the only value that works, leading to n = 5 as the sole integer solution. The video concludes with a reminder to engage with the content by commenting, liking, and subscribing.
Takeaways
- 🧩 The video is focused on solving a factorial equation: \( n! + (n-2)! = n^3 + 1 \) for non-negative integer values of \( n \).
- 🔍 The presenter initially suggests plugging in values as a trial-and-error method but acknowledges it may not be efficient or exhaustive.
- 📈 A graph is mentioned, but it does not show integer solutions, and Wolfram Alpha is cited for suggesting a non-integer solution of approximately 1.37.
- 📚 The gamma function is introduced as a way to define factorial for all real numbers, but the focus remains on integer solutions.
- 🔑 Factorials are divisible by smaller factorials, which is a key property used to simplify the equation.
- ✂️ The equation is manipulated by expressing \( n! \) in terms of \( (n-2)! \) and then factoring out common terms.
- 🔄 The presenter simplifies the equation to \( n^2 - n + 1 \) on the left side and factors \( n^3 + 1 \) on the right side using the sum of cubes formula.
- 🎯 The equation simplifies to a form where a common factor \( n^2 - n + 1 \) can be canceled out, leading to a simpler equation.
- 🔄 Substitution is used to replace \( n - 2 \) with \( k \) and \( n + 1 \) with \( k + 3 \) to further simplify the problem.
- 📉 The presenter explores different values of \( k \) to find integer solutions, considering both positive and negative values.
- 🎯 The only value of \( k \) that works is 3, leading to the conclusion that \( n = 5 \) is the only integer solution to the equation.
Q & A
What is the equation being solved in the video?
-The equation being solved is n factorial + (n - 2) factorial = n^3 + 1, where n is a non-negative integer.
What is the smallest value that n can be in the given equation?
-The smallest value that n can be is zero, as n is a non-negative integer.
What did Wolfram Alpha initially suggest regarding the integer solutions for the equation?
-Wolfram Alpha initially suggested that there might not be any integer solutions, only providing a non-integer solution of approximately 1.37.
How is the gamma function mentioned in the video relevant to the problem?
-The gamma function is relevant because it allows the definition of the factorial function for all real numbers, not just integers.
What algebraic identity is used to factor n^3 + 1 in the video?
-The algebraic identity used to factor n^3 + 1 is the sum of cubes formula, which states that a^3 + b^3 = (a + b)(a^2 - ab + b^2).
What is the significance of the common factor n - 2 factorial in simplifying the equation?
-The common factor n - 2 factorial is significant because it allows for the simplification of the equation by factoring out this term and making the equation easier to solve.
What substitution is made to simplify the equation further?
-The substitution made is to let n - 2 = k, which implies n = k + 2 and n + 1 = k + 3.
What is the smallest value that k can be to find a non-negative integer solution?
-The smallest value that k can be is 1, because k = 0 would not work as it would lead to a factorial of zero which is not valid in this context.
What are the possible values for k that lead to integer solutions?
-The possible values for k that lead to integer solutions are 1 and 3, as these are the only values that, when substituted back into the equation, yield a valid factorial expression.
What is the only integer solution found for n in the video?
-The only integer solution found for n is 5, as it is the result of k = 3, which leads to n = k + 2 = 5.
Outlines
🧮 Introduction to the Factorial Equation
The video begins with an introduction to solving a factorial equation involving the expression n factorial + (N - 2) factorial = n^3 + 1, where n is a non-negative integer. The presenter suggests that plugging in values to guess and check may not be efficient for all solutions. They also mention that while Wolfram Alpha suggests there might not be an integer solution, the equation can be analyzed further. The factorial function is noted to be defined for all real numbers using the gamma function, but the focus remains on integer solutions. The presenter then starts to factor the equation and simplify it by expressing factorials in terms of products and divisibility.
🔍 Factoring and Simplifying the Equation
The presenter continues by factoring out n - 2 factorial from both terms on the left side of the equation, which leads to an expression involving n^2 - n + 1. They then factor n^3 + 1 on the right side as (n + 1)(n^2 - n + 1), revealing a common factor. The video discusses the possibility of the common factor being zero, which simplifies the equation further. The presenter uses substitution, setting n - 2 equal to K, to transform the equation and explore potential integer solutions. They also consider the implications of K being 1 or 3, and test these values to find feasible solutions.
🎓 Conclusion and Final Solution
After a detailed exploration and testing of different values for K, the presenter concludes that the only value that works is when K equals 3, which implies n - 2 equals 3, and therefore n equals 5. This finding leads to the only integer solution for the given equation. The video ends with a reminder to the viewers to engage with the content by commenting, liking, and subscribing, and the presenter bids farewell until the next video.
Mindmap
Keywords
💡Factorial
💡Equation
💡Graph
💡Gamma Function
💡Integer Solution
💡Factoring
💡Sum of Cubes
💡Substitution
💡Prime Number
💡Combinatorics
Highlights
The video aims to solve a factorial equation for integer values of n.
The equation is n factorial + (n - 2) factorial = n^3 + 1.
From Alpha suggests there may not be an integer solution, only a non-integer at 1.37.
The gamma function extends the factorial to real numbers but the search is for integer solutions.
Factorials contain smaller factorials and are divisible by them.
n factorial can be expanded and expressed in terms of (n - 2) factorial.
The equation is simplified by factoring out common terms.
n^3 + 1 is factorable using the sum of cubes formula.
The video introduces a substitution method to simplify the equation.
n - 2 is substituted with k, leading to n = k + 2 and n + 1 = k + 3.
Factorials grow faster than polynomials, which can hint at potential solutions.
K factorial is expanded and simplified by factoring out k and k - 1 factorial.
The product simplifies to 3, indicating potential integer solutions for k.
k cannot be 0, 1, or negative as it would not satisfy the equation.
k = 3 is tested and found to be a valid solution, leading to n = 5.
The only integer solution to the equation is n = 5.
The video concludes with the solution and a reminder to engage with the content.
Transcripts
Browse More Related Video
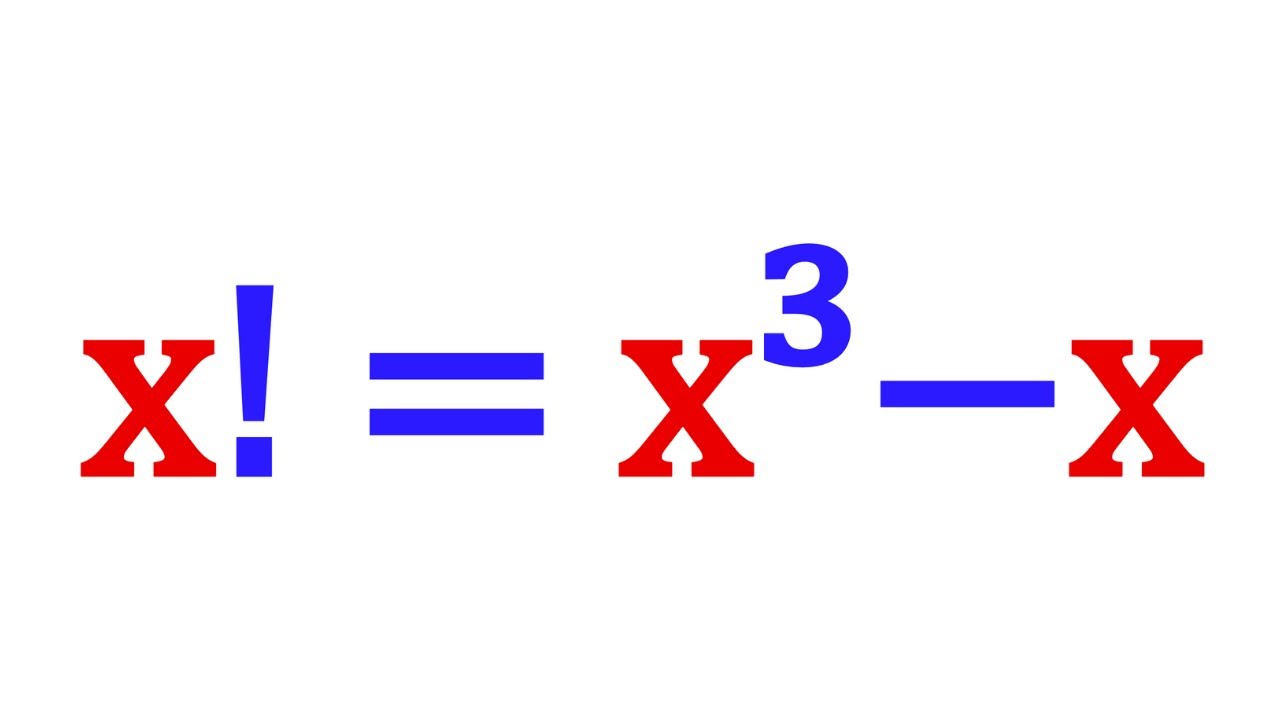
Can We Solve A Nice Factorial Equation

Solving Polynomial and Rational Equations

Solving the logistic differential equation part 2 | Khan Academy

An Interesting Olympiad Problem With Factorials
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (34 of 92) Finite Potential Well Part 3

Proof by Mathematical Induction | Principle of Mathematical Induction | Sample Problems | Part 1
5.0 / 5 (0 votes)
Thanks for rating: