Two-Way ANOVA - Full Course

DATAtab

22 Oct 202316:20

EducationalLearning

32 Likes 10 Comments

TLDRThis video explains the two-way ANOVA, a statistical method used to analyze the effect of two categorical variables on a continuous variable. It compares this with the one-way ANOVA, detailing how the two-way ANOVA tests for interaction effects between the variables. The video covers null and alternative hypotheses, assumptions for valid results, and the calculation process. Examples include testing drug type and gender on blood pressure reduction. It highlights interpreting results using statistical software and explains the importance of variance in the analysis.

Takeaways

📊 A two-way ANOVA is a statistical method used to test the effect of two categorical variables on a continuous variable.
📈 The categorical variables in a two-way ANOVA are called factors, and the continuous variable is the dependent variable.
🔍 A one-way ANOVA tests the effect of a single independent variable on a dependent variable, while a two-way ANOVA tests the effects of two independent variables.
💡 Factors are nominal variables, such as gender (male, female), type of therapy (A, B, C), or field of study (medicine, business, psychology).
🔬 Use ANOVA to test whether the levels of a factor have an influence on the dependent variable, such as the effect of gender on salary or therapy type on blood pressure.
🧪 A two-way ANOVA is used when there are two factors, and it tests whether each factor and their interaction have an effect on the dependent variable.
📉 The two-way ANOVA can answer three questions: the effect of the first factor, the effect of the second factor, and the interaction effect between the two factors on the dependent variable.
📊 In a two-way ANOVA, there are three null hypotheses: no significant difference for the first factor, no significant difference for the second factor, and no interaction effect.
🔍 Assumptions for a valid two-way ANOVA include normality, homogeneity of variances, independence of measurements, and the dependent variable should be on a metric scale.
💻 To calculate a two-way ANOVA, you can use statistical software or perform the calculations by hand, considering the main effects and interaction effects on the dependent variable.

Q & A

What is a two-way ANOVA used for?
-A two-way ANOVA is used to test the effect of two categorical variables on a continuous variable. It is an extension of the one-way ANOVA, which tests the effect of a single independent variable on a dependent variable.
What are the two independent variables in a two-way ANOVA called?
-The two independent variables in a two-way ANOVA are called factors. Examples of factors include gender (with levels male and female), type of therapy (with levels A, B, C), or field of study (with levels medicine, business administration, psychology, mathematics).
What is a factor in the context of ANOVA?
-A factor in ANOVA is a nominal variable that is used to create different levels or groups for testing their influence on the dependent variable. Factors can include things like gender, type of therapy, or field of study.
When would you use a one-way ANOVA instead of a two-way ANOVA?
-You would use a one-way ANOVA when you have only one factor to test its effect on the dependent variable. For example, if you want to test whether gender has an effect on salary, you would use a one-way ANOVA.
What additional information does a two-way ANOVA provide compared to a one-way ANOVA?
-A two-way ANOVA not only tests the main effects of each factor on the dependent variable but also tests for an interaction effect between the two factors. This means it can tell you if the effect of one factor depends on the level of the other factor.
What are the three null hypotheses tested in a two-way ANOVA?
-The three null hypotheses in a two-way ANOVA are: 1) There is no significant difference between the groups of the first factor. 2) There is no significant difference between the groups of the second factor. 3) There is no interaction effect between the two factors.
What assumptions must be met for a two-way ANOVA to be valid?
-For a two-way ANOVA to be valid, several assumptions must be met: 1) Normality - the data within the groups should be normally distributed. 2) Homogeneity of variances - the variance of data in groups should be equal. 3) Independence - the measurements should be independent. 4) Measurement level - the dependent variable should have a metric scale level.
How can you check if the assumption of normality is met in a two-way ANOVA?
-Normality can be checked with a quantile-quantile plot, which helps to determine if the data within the groups are normally distributed or if the residuals are normally distributed.
What is the purpose of calculating sum of squares (SS) in a two-way ANOVA?
-In a two-way ANOVA, the total variance of the dependent variable is divided into variance that can be explained by factor A, factor B, their interaction, and the error variance. The sum of squares (SS) is used to quantify these different components of variance.
How do you interpret the results of a two-way ANOVA in terms of P values?
-If the calculated P value for any of the factors or the interaction is less than the significance level (commonly set at 5%), the null hypothesis is rejected, indicating a significant effect. If the P value is greater than 0.05, the null hypothesis is not rejected, indicating no significant effect.
Can you provide an example of how to calculate a two-way ANOVA by hand?
-Yes, the example given in the script involves calculating the mean values for each group, then calculating the sum of squares for total, between groups, for each factor, the interaction, and the error. The F values are then calculated by dividing the variance of each factor or interaction by the error variance, and P values are determined using these F values and their corresponding degrees of freedom.

Outlines

00:00

📊 Introduction to Two-Way ANOVA

A two-way ANOVA is a statistical method used to examine the effect of two categorical variables (independent variables) on a continuous variable (dependent variable). It extends the one-way ANOVA by testing the impact of two factors, such as drug type and gender on blood pressure reduction. The independent variables are called factors, and each factor can have multiple levels. This analysis helps determine if the factors and their interactions significantly affect the dependent variable.

05:02

📋 Assumptions for Two-Way ANOVA

For the results of a two-way ANOVA to be valid, several assumptions must be met: (1) Normality: data within groups should be normally distributed; (2) Homogeneity of variances: variances in groups should be equal, checked with the Levene test; (3) Independence: measurements should be independent; (4) Measurement level: the dependent variable should be on a metric scale. The process involves collecting data, assigning patients to treatment combinations, and measuring outcomes.

10:05

🧮 Calculating Two-Way ANOVA

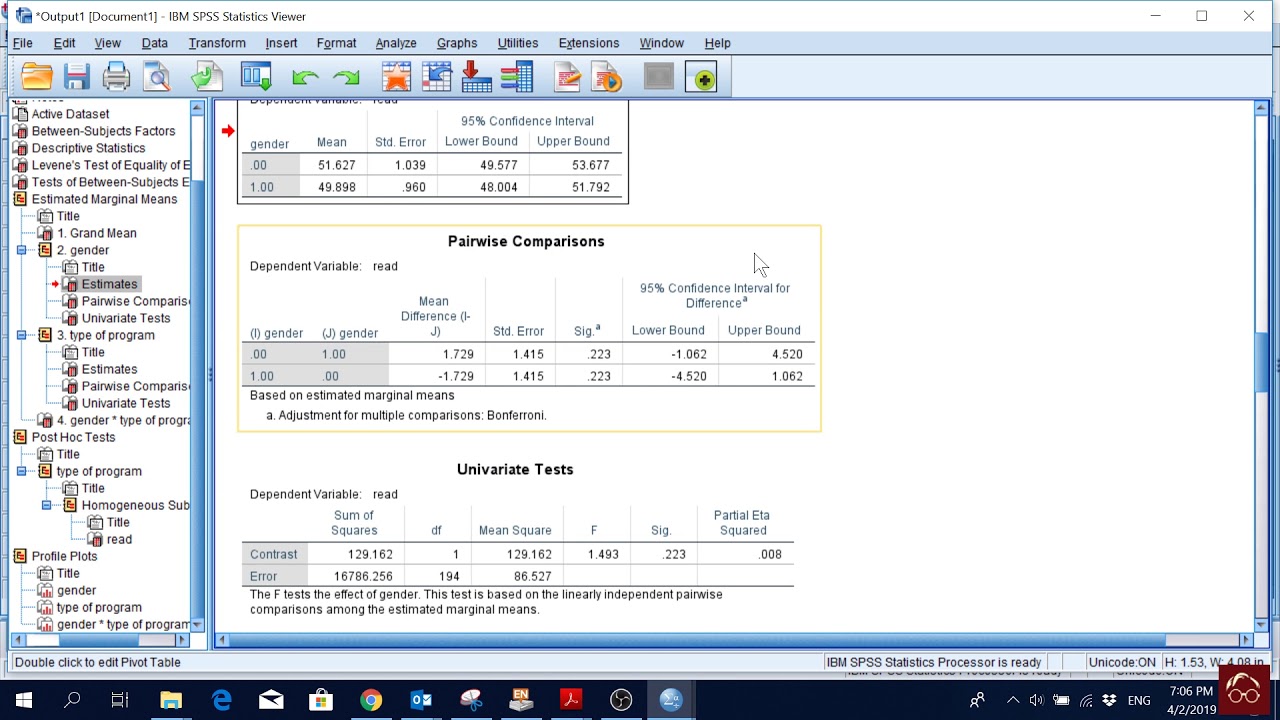
To calculate a two-way ANOVA, collect data, assign patients to treatments, and measure outcomes. Statistical software can be used to perform the calculations, which involve determining the mean values for each group and overall, calculating sums of squares, and evaluating the variances. The analysis helps determine the effects of factors and their interactions on the dependent variable. If the p-value is less than the significance level, the null hypothesis is rejected, indicating a significant effect.

15:07

🔢 Interpreting Two-Way ANOVA Results

The results of a two-way ANOVA are presented in a table that shows the effects of each factor and their interaction on the dependent variable. P-values are used to determine the significance of these effects. If the p-value is greater than the significance level, the null hypothesis is not rejected, indicating no significant effect. The analysis involves dividing the total variance into components attributed to each factor, their interaction, and error variance, helping to explain the variance in the dependent variable.

Mindmap

Keywords

💡Two-way ANOVA

Two-way ANOVA, or Analysis of Variance, is a statistical method used to test the effect of two categorical independent variables on a continuous dependent variable. It extends the one-way ANOVA by analyzing the impact of two factors simultaneously. In the context of the video, it is used to determine if 'drug type' and 'gender' have an effect on 'blood pressure reduction'. The script explains that a two-way ANOVA allows researchers to assess not only the main effects of each factor but also the interaction effect between them.

💡Categorical Variables

Categorical variables are types of data that can be categorized into distinct groups. In the script, 'drug type' with categories 'drug A' and 'drug B' and 'gender' with categories 'male' and 'female' are examples of categorical variables. These are the independent variables in a two-way ANOVA, and the video discusses how they can influence the dependent variable, which in this case is the reduction in blood pressure.

💡Continuous Variable

A continuous variable is a type of data that can take on any value within a range and is measured on a numerical scale. In the video, 'blood pressure reduction' is the continuous variable that the two-way ANOVA is testing against. It is the outcome that researchers are interested in understanding how it is affected by the categorical variables of drug type and gender.

💡Independent Variables

Independent variables are factors that are manipulated or selected by the researcher to observe their effect on the dependent variable. In the video script, 'drug type' and 'gender' are the independent variables. They are the factors that the two-way ANOVA is designed to test for their impact on the dependent variable, which is the reduction in blood pressure.

💡Dependent Variable

The dependent variable is the outcome that is being measured in an experiment and is expected to change as a result of the independent variables. In the context of the video, 'blood pressure reduction' is the dependent variable. The script explains that researchers use two-way ANOVA to test whether changes in the independent variables (drug type and gender) lead to changes in this dependent variable.

💡Factors

In the context of ANOVA, factors refer to the independent variables being tested. The video script mentions 'gender', 'type of therapy', and 'field of study' as examples of factors. These are nominal variables with different levels (e.g., male and female for gender) that researchers use to categorize their experimental groups and analyze their effects on the dependent variable.

💡Interaction Effect

Interaction effect in a two-way ANOVA refers to the situation where the effect of one independent variable depends on the level of the other independent variable. The video script explains that researchers can use two-way ANOVA to determine if there is an interaction effect between 'drug type' and 'gender' on the reduction in blood pressure, meaning that the effect of one factor might be different at different levels of the other factor.

💡Null Hypotheses

Null hypotheses are statements of no effect or no difference that are tested in an ANOVA. The video script outlines three null hypotheses for a two-way ANOVA: no significant difference between the groups of the first factor, no significant difference between the groups of the second factor, and no interaction effect between the two factors. These hypotheses are tested against their alternative hypotheses to determine if there is a significant effect.

💡Assumptions

Assumptions are conditions that must be met for the results of a statistical test to be valid. The video script mentions several assumptions for two-way ANOVA, including normality (data within groups should be normally distributed), homogeneity of variances (variances of data in groups should be equal), independence (measurements should be independent), and measurement level (the dependent variable should have a metric scale level). These assumptions are crucial for the validity of the ANOVA results.

💡Sum of Squares

Sum of Squares (SS) is a measure used in ANOVA that represents the total variability in the data. In the video script, it is explained that the total sum of squares is the sum of the squared differences between each individual value and the total mean. The script further details how to calculate the sum of squares for each factor, the interaction, and the error, which are all components of the total sum of squares.

💡Degrees of Freedom

Degrees of freedom (df) in the context of ANOVA refer to the number of independent values in a data set that can vary without restriction. The video script explains how to calculate degrees of freedom for the total variance, sum of squares between groups, and sum of squares for each factor and interaction. Degrees of freedom are used to calculate the variance and the F-value, which are critical for hypothesis testing in ANOVA.

💡F-value

The F-value is a statistical measure used in ANOVA to test the null hypotheses. It is calculated by dividing the variance of a factor or interaction by the error variance. The video script describes how to calculate the F-value for each factor and interaction effect and how these values are used to determine if the null hypotheses can be rejected based on the significance level.

💡P-value

The P-value is the probability of observing the data, or something more extreme, assuming that the null hypothesis is true. In the context of the video, the P-value is used to determine whether the results of the two-way ANOVA are statistically significant. The script explains that if the calculated P-value is less than the significance level (e.g., 0.05), the null hypothesis is rejected, indicating a significant effect.

Highlights

Two-way ANOVA is a statistical method used to test the effect of two categorical variables on a continuous variable.

Categorical variables are the independent variables, and the continuous variable is the dependent variable.

One-way ANOVA tests the effect of a single independent variable, while two-way ANOVA tests the effects of two independent variables.

Independent variables in ANOVA are referred to as factors, which are nominal variables.

A two-way ANOVA is used when there is a second factor and its effect on the dependent variable is also of interest.

The groups in a two-way ANOVA result from the combination of the levels of the two factors.

A two-way ANOVA can answer whether the first factor, the second factor, or their interaction effect has an impact on the dependent variable.

There are three null hypotheses and three alternative hypotheses in a two-way ANOVA.

Assumptions for a valid two-way ANOVA include normality, homogeneity of variances, independence, and a metric scale level for the dependent variable.

Examples of using a two-way ANOVA include testing the effect of drug type and gender on blood pressure reduction.

Statistical software like DataTab can be used to calculate and interpret two-way ANOVA results.

Descriptive statistics and the Levene test can be used to check the equality of variances within groups.

The results of the ANOVA provide P values to determine if the null hypotheses can be rejected.

The analysis of variance divides the total variance into variance explained by each factor, their interaction, and error variance.

Sum of squares, F values, and P values are calculated to determine the statistical significance of factors and their interaction.

The calculation of sum of squares, variance, and F values involves specific formulas and steps.

Critical F values can be found in tables or calculated using software to determine the P values.

Transcripts

Browse More Related Video

SPSS (11): Two-Way ANOVA (Interaction Effect of Two Categorical Variables)

Two-Way ANOVA - all Equations - calculated by Hand

Two factor ANOVA with repeated measures

One Factor vs. Two Factor ANOVA [One Way vs Two Way]

ANOVA (Analysis of variance) simply explained

Two Factor ANOVA [without repeated measures]