SPSS (11): Two-Way ANOVA (Interaction Effect of Two Categorical Variables)
TLDRThis instructional video demonstrates how to conduct a two-way ANOVA to explore the interaction effect between two categorical variables, gender and program type, on a continuous dependent variable such as reading scores. The tutorial guides viewers through the process in a statistical software, from selecting variables and plotting to interpreting the results, including post hoc tests and profile plots. The analysis reveals no significant interaction effect, with program type explaining the most variance in reading scores, while gender does not significantly impact the outcome.
Takeaways
- 🔍 The video demonstrates how to perform a two-way ANOVA to analyze the interaction effect between two categorical variables on a continuous dependent variable.
- 📊 The example used in the video involves examining the interaction effect between gender and program type on reading scores.
- 💡 To conduct the two-way ANOVA, one must navigate to the 'General Linear Model' and select 'Univariate' in the statistical software.
- 📝 The dependent variable in this case is the reading score, with gender and program type as the two categorical independent variables.
- 📈 Plots are used to visualize the means of the dependent variable across different categories of the independent variables and their interaction.
- 🔑 Post hoc tests are relevant for the variable with more than two categories, in this case, the program type, to determine which categories differ significantly from each other.
- 📉 The assumption of equal variances across groups is tested using Levene's test, and the results indicate that the assumption holds for this dataset.
- 🚫 The main results show that gender does not have a significant effect on reading scores, but program type does, and the interaction effect is not significant.
- 📊 The partial eta squared values indicate the proportion of variance in the dependent variable explained by each independent variable and their interaction.
- 📋 Descriptive statistics, such as means, standard deviations, and confidence intervals, are provided for each category of the independent variables.
- 📊 Profile plots are used to visually assess the interaction effect, and in this case, they suggest no significant interaction between gender and program type on reading scores.
Q & A
What is a two-way ANOVA used for?
-A two-way ANOVA is used to analyze the interaction effect between two categorical variables on a continuous dependent variable.
What are the categorical variables considered in the script for the two-way ANOVA example?
-The categorical variables considered are gender (with categories male and female) and program type (with categories vocational, academic, and general).
What is the dependent variable in the example provided in the script?
-The dependent variable in the example is the reading score.
What is meant by 'interaction effect' in the context of two-way ANOVA?
-An interaction effect refers to the situation where the effect of one independent variable on the dependent variable depends on the level of another independent variable.
What is the purpose of the Levene's test in the context of ANOVA?
-Levene's test is used to check the assumption of homogeneity of variances across groups. It tests the null hypothesis that the variances of the groups are equal.
What does it mean if the p-value in Levene's test is higher than 0.05?
-If the p-value is higher than 0.05, it means that we fail to reject the null hypothesis, indicating that the variances across groups are considered equal.
What is the significance of partial eta squared in the context of ANOVA?
-Partial eta squared is a measure of effect size that represents the proportion of variance in the dependent variable that is explained by each independent variable, adjusted for other variables in the model.
What does it mean if the p-value for the interaction term in ANOVA is higher than 0.05?
-If the p-value for the interaction term is higher than 0.05, it suggests that there is no significant interaction effect between the two independent variables on the dependent variable.
What is the purpose of post hoc tests in ANOVA?
-Post hoc tests are used to determine which specific groups differ from each other after finding a significant effect in ANOVA, especially when there are more than two categories in an independent variable.
What can be inferred from the profile plots in the script?
-Profile plots help visualize the estimated means of the dependent variable across different levels of the independent variables. If lines in the plot do not intersect, it suggests no significant interaction effect between the variables.
What is the conclusion about the interaction effect between gender and program type on reading scores based on the script?
-Based on the script, there is no significant interaction effect between gender and program type on reading scores, as both genders show similar patterns of performance across the different program types.
Outlines
📊 Two-Way ANOVA Setup and Assumptions
This paragraph introduces the process of conducting a two-way ANOVA to analyze the interaction effect between two categorical variables, gender and program type, on a continuous dependent variable, reading score. The speaker explains navigating the 'Analyze' menu to select 'General Linear Model' and 'Univariate', choosing the dependent variable, and setting up categorical variables with their respective categories. The importance of plotting mean scores and considering interaction effects is highlighted. The paragraph also discusses post hoc tests for program types, the assumption of equal variances, and the selection of confidence interval adjustments. The descriptive statistics, including frequencies and means, are presented, suggesting a pattern that might not indicate a significant interaction effect.
🔍 Analyzing Results and Interpreting Two-Way ANOVA Outcomes
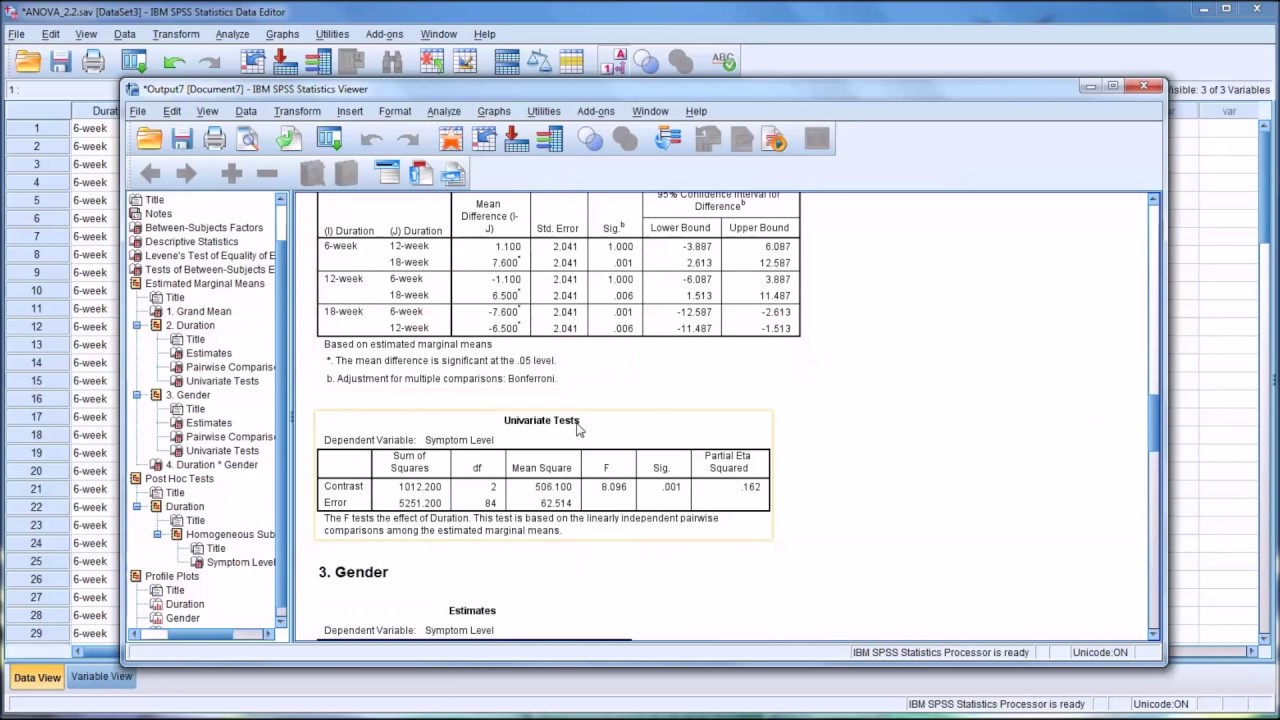
The second paragraph delves into the results of the two-way ANOVA, discussing the significance levels and the effects of gender and program type on reading scores. It is revealed that gender does not significantly affect reading scores, while program type does. The interaction effect between gender and program type is not significant, as indicated by the p-values and partial ETA squared values. The paragraph also covers the stimulated marginal means, pairwise comparisons, and univariate tests, which further confirm the lack of a significant interaction effect. Post hoc tests and profile plots are used to illustrate the differences between program types, with academic programs scoring the highest and vocational the lowest, regardless of gender.
📈 Visualizing Data and Concluding the Two-Way ANOVA Analysis
The final paragraph focuses on visualizing the data through profile plots and discussing the implications of the findings. It emphasizes the lack of intersection in the lines of the plot, which suggests no significant interaction effect between gender and program type on reading scores. The academic program consistently scores higher, while the vocational program scores lower, with no differences observed between genders across program types. The speaker concludes by summarizing the findings and inviting viewers to engage with the content by liking, commenting, sharing, and subscribing to the channel.
Mindmap
Keywords
💡Two-way ANOVA
💡Categorical Variables
💡Continuous Dependent Variable
💡Interaction Effect
💡Univariate
💡Descriptive Statistics
💡Post Hoc Test
💡Partial Eta Squared
💡Homogeneity of Variance
💡Profile Plots
Highlights
Introduction to running a two-way ANOVA to examine the interaction effect between two categorical variables on a continuous dependent variable.
Demonstration of selecting the 'General Linear Model' and 'Univariate' options in statistical software to perform a two-way ANOVA.
Selection of 'Reading Score' as the dependent variable and 'Gender' and 'Program Type' as categorical independent variables.
Explanation of choosing plots to visualize the mean of reading scores for gender and program types, including interaction terms.
Discussion on the relevance of post hoc tests for 'Program Type' due to its three categories, unlike the binary 'Gender'.
Assumption of equality variance for the analysis and choice of the Games-Howell post hoc test.
Inclusion of descriptive statistics, effect size estimates, and homogeneity tests in the analysis options.
Presentation of subject frequencies and descriptive statistics for gender and program types, including mean scores and standard deviations.
Observation of similar patterns in reading scores across gender and program types, suggesting a potential lack of significant interaction effect.
Conducting Levene's test for equality of variance and its significance in the context of two-way ANOVA assumptions.
Acceptance of the null hypothesis in Levene's test, indicating equal variance across groups.
Results of the two-way ANOVA test, showing no significant effect of 'Gender' but a significant effect of 'Program Type' on reading scores.
Interpretation of partial eta squared values to understand the percentage of variation explained by each variable and their interaction.
Analysis of stimulated marginal means to compare the main effects of gender and program type on reading scores.
Pairwise comparisons revealing significant differences between 'General' and 'Academic' programs, but not between 'General' and 'Vocational'.
Univariate tests confirming the significant effect of 'Program Type' on reading scores and its contribution to the variation.
Descriptive statistics of the interaction terms between 'Gender' and 'Program Type', showing similar patterns for both genders.
Post hoc test results using homogeneous subsets, indicating no significant difference between 'General' and 'Vocational' program types.
Profile plots visualizing the estimated means of reading scores, showing no interaction effect between gender and program type.
Conclusion that there is no significant interaction effect between gender and type of program on reading scores.
Call to action for viewers to like, comment, share, and subscribe for more informative content.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: