Using a table to estimate P-value from t statistic | AP Statistics | Khan Academy

Khan Academy

20 Feb 201804:52

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses a statistical hypothesis testing scenario where Caterina is testing a null hypothesis that the population mean is equal to zero against an alternative hypothesis that it is not. With a sample size of six, she calculates a T statistic of 2.75. The script explains the process of finding the P-value by considering the T distribution, degrees of freedom (sample size minus one), and looking up critical values in a T table. It emphasizes that the P-value is the sum of the probabilities of getting a T value at least 2.75 above or below the mean, which is approximately 0.04 in this case. The final step is to compare this P-value to the significance level set by Caterina to decide whether to reject or not reject the null hypothesis.

Takeaways

🔍 Caterina's null hypothesis is that the true population mean of a dataset is equal to zero, while her alternative hypothesis is that it's not equal to zero.
📐 She takes a sample of six observations to test her null hypothesis and calculates a test statistic (T value) of 2.75.
✅ The conditions for statistical inference are assumed to be met, allowing for the calculation of the P-value.
🧮 The T value is calculated by dividing the difference between the sample mean and the assumed population mean (from the null hypothesis) by the estimated standard deviation of the sampling distribution.
📊 The estimated standard deviation is the sample standard deviation divided by the square root of the sample size (N).
📉 To find the P-value, Caterina considers the probability of getting a T value that is 2.75 or more above or below the mean, due to a two-tailed test.
📚 A T-table is used to find the critical values and corresponding tail probabilities, which are based on degrees of freedom (sample size minus one).
🔢 For a sample size of six, the degrees of freedom are five, and the T-table is used to find the probability associated with a T value of 2.75.
🔑 The tail probability from the T-table for the T value of 2.75 is between 0.025 and 0.02, with a closer approximation to 0.02.
🧮 The P-value for Caterina's test is approximately the sum of the two tail probabilities, which is about 0.04.
✅ Caterina compares the P-value to her predetermined significance level to decide whether to reject the null hypothesis in favor of the alternative.

Q & A

What is Caterina's null hypothesis in the test?
-Caterina's null hypothesis is that the true population mean of the data set is equal to zero.
What is the alternative hypothesis to Caterina's null hypothesis?
-The alternative hypothesis is that the true population mean is not equal to zero.
What sample size did Caterina use for her test?
-Caterina used a sample size of six observations for her test.
What is the test statistic (T value) that Caterina obtained from her sample?
-The test statistic (T value) obtained from Caterina's sample is 2.75.
What is the formula for calculating the T value in Caterina's test?
-The T value is calculated as the difference between the sample mean and the assumed population mean (from the null hypothesis), divided by the estimated standard deviation of the sampling distribution, which is the sample standard deviation divided by the square root of the sample size (N).
What are the degrees of freedom in Caterina's test?
-The degrees of freedom in Caterina's test are the sample size minus one, which in this case is 6 - 1 = 5.
How does the T distribution differ from the Z distribution?
-The T distribution differs from the Z distribution in that it accounts for smaller sample sizes and is used when the population standard deviation is unknown. It also has different critical values and is more spread out than the Z distribution.
What does Caterina need to look up in the T table to find the P-value?
-Caterina needs to look up the T value of 2.75 in the T table corresponding to the degrees of freedom, which is 5 in this case.
What is the approximate P-value for Caterina's test, according to the T table?
-The approximate P-value for Caterina's test is the sum of the probabilities in the two tails of the T distribution that are at least 2.75 units away from the mean, which is approximately 0.04.
What does Caterina do with the P-value in relation to her significance level?
-Caterina compares the P-value to her predetermined significance level. If the P-value is lower than the significance level, she rejects the null hypothesis and accepts the alternative hypothesis. If the P-value is not lower, she does not reject the null hypothesis.
What does it mean if Caterina rejects the null hypothesis?
-If Caterina rejects the null hypothesis, it suggests that there is sufficient evidence to support the alternative hypothesis, meaning that the true population mean is not equal to zero.
What does it imply if Caterina does not reject the null hypothesis?
-If Caterina does not reject the null hypothesis, it implies that there is not enough evidence to suggest that the true population mean is different from zero, and the results could be due to chance.

Outlines

00:00

🔍 Hypothesis Testing with Sample Data

In this paragraph, the instructor introduces Caterina's hypothesis testing scenario. Caterina's null hypothesis posits that the population mean of a certain dataset is zero, while her alternative hypothesis suggests it is not. She takes a sample of six observations and calculates a T statistic of 2.75, assuming the conditions for statistical inference are met. The task at hand is to determine the approximate P-value for Caterina's test. The concept of the T statistic is explained, which is the difference between the sample mean and the assumed population mean from the null hypothesis, divided by the estimated standard error of the sampling distribution. The instructor emphasizes the need to consider both tails of the T distribution when calculating the P-value, which is the probability of observing a T statistic as extreme as 2.75 or more in either direction from the mean. A T table is used to find the critical values and corresponding tail probabilities, which are then summed to estimate the P-value.

Mindmap

Keywords

💡Null Hypothesis

The null hypothesis is a fundamental concept in statistical testing. It is a statement of no effect or no difference that is used as a starting point for statistical analysis. In the video, Caterina's null hypothesis is that the true population mean of her data set is equal to zero. This serves as the basis for her statistical test, and if the evidence from her sample is strong enough, she may reject this hypothesis in favor of her alternative hypothesis.

💡Alternative Hypothesis

The alternative hypothesis is the statement that is considered when the null hypothesis is rejected. It proposes an effect or a difference that contrasts with the null hypothesis. In the context of the video, Caterina's alternative hypothesis is that the population mean is not equal to zero, which she wants to prove if the statistical evidence from her sample supports it.

💡Sample Size

Sample size refers to the number of observations or elements in a sample. It plays a critical role in determining the power of a statistical test and the reliability of its results. In the video, Caterina takes a sample of six observations, which is the basis for her calculation of the sample mean and standard deviation.

💡Test Statistic

A test statistic is a numerical value computed from a sample of data that is used to make inferences about a population. In the video, the test statistic Caterina uses is denoted as 'T', which is equal to 2.75. This value is crucial for determining the P-value and making a decision about the null hypothesis.

💡P-value

The P-value is the probability of obtaining results as extreme as, or more extreme than, the observed results under the assumption that the null hypothesis is true. A low P-value indicates strong evidence against the null hypothesis. In the video, Caterina is trying to find the P-value for her test statistic T, which is approximately 0.04, suggesting significant evidence against her null hypothesis.

💡Degrees of Freedom

Degrees of freedom in statistics refer to the number of values in the data that are free to vary independently. It is a key concept in hypothesis testing and is used in the calculation of various statistics, including the T-value. In the video, the degrees of freedom for Caterina's sample is six minus one, which equals five.

💡T Distribution

The T distribution, also known as the Student's t-distribution, is a type of probability distribution that is used in statistical inference when the sample size is small and population standard deviation is unknown. It is symmetric and bell-shaped. In the video, Caterina uses the T distribution to find the critical value corresponding to her T statistic and to calculate the P-value.

💡Sample Mean

The sample mean is the average of the values in a sample, calculated by adding all the values together and dividing by the number of values. It is used to estimate the population mean. In the video, Caterina calculates the sample mean from her six observations to estimate the population mean, which is central to her hypothesis test.

💡Sample Standard Deviation

The sample standard deviation is a measure of the amount of variation or dispersion in a set of values. It is an estimate of the standard deviation of the population from which the sample is drawn. In the video, Caterina calculates the sample standard deviation to help determine her T statistic.

💡Significance Level

The significance level is a threshold probability used in hypothesis testing to decide whether to reject the null hypothesis. It is often denoted by the Greek letter alpha (α). If the P-value is less than the significance level, the null hypothesis is rejected. In the video, Caterina would compare her calculated P-value to her predetermined significance level to make her decision.

💡Rejection of Null Hypothesis

The rejection of the null hypothesis occurs when the statistical evidence is strong enough to suggest that the alternative hypothesis is more likely to be true. If the P-value is less than the significance level, the null hypothesis is typically rejected. In the context of the video, if Caterina's P-value of approximately 0.04 is lower than her significance level, she would reject the null hypothesis.

Highlights

Caterina is testing a null hypothesis that the true population mean of a data set is equal to zero.

The alternative hypothesis is that the population mean is not equal to zero.

A sample of six observations is taken to test the null hypothesis.

The test statistic T is calculated to be 2.75 based on the sample.

The conditions for statistical inference are assumed to be met.

The T value is calculated as the difference between the sample mean and the null hypothesis mean (0), divided by the estimated standard error.

The estimated standard error is the sample standard deviation divided by the square root of the sample size (N).

The T distribution is used instead of the Z distribution because we are estimating the population standard deviation.

The degrees of freedom for the T distribution is the sample size minus one (N-1).

For this example, the degrees of freedom is 5 (sample size of 6 minus 1).

The T value of 2.75 is looked up in the T distribution table for the corresponding tail probabilities.

The tail probability for a T value of 2.75 with 5 degrees of freedom is between 0.025 and 0.02.

The T distribution is symmetric, so the tail probabilities on both sides are approximately equal.

The P-value for the test is the sum of the tail probabilities, which is approximately 0.04.

If the P-value is less than the significance level, the null hypothesis is rejected in favor of the alternative hypothesis.

If the P-value is not less than the significance level, the null hypothesis cannot be rejected.

The significance level is predetermined before conducting the hypothesis test.

This example demonstrates the process of hypothesis testing using a T-test for a sample mean.

Transcripts

Browse More Related Video

Explaining The One-Sample t-Test

Test Statistic For Means and Population Proportions

P-values and significance tests | AP Statistics | Khan Academy

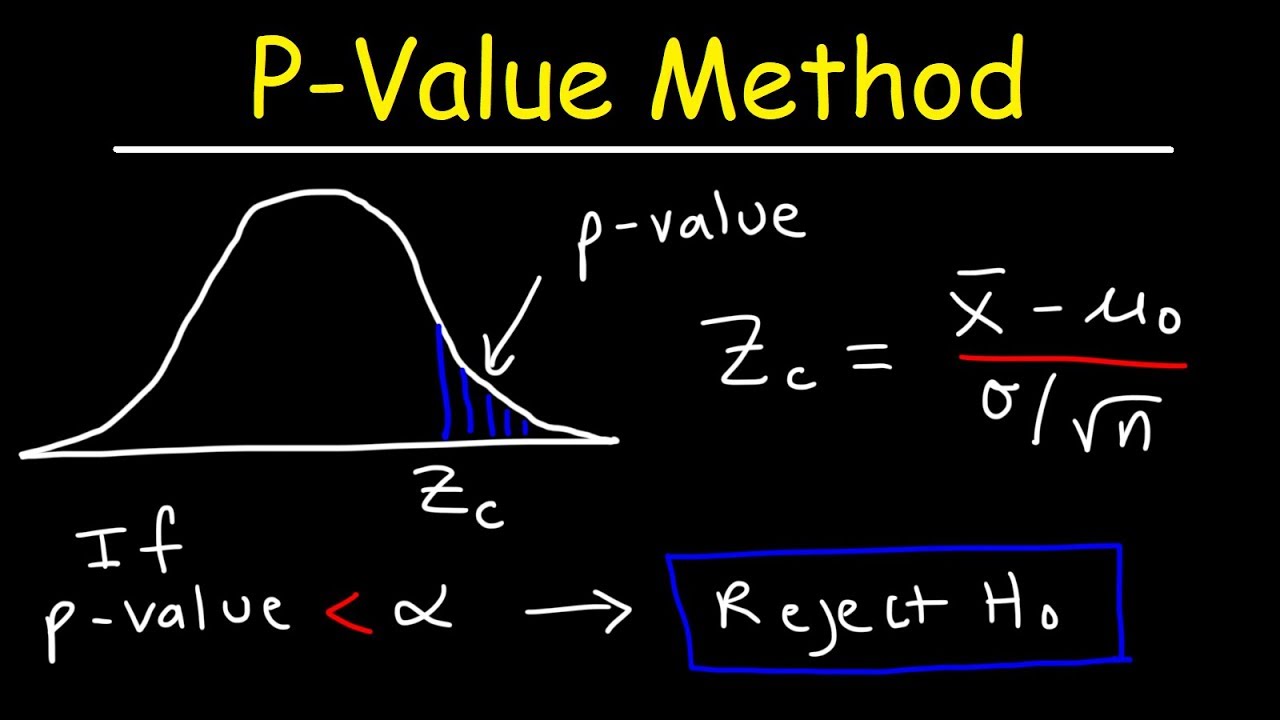
P-Value Method For Hypothesis Testing

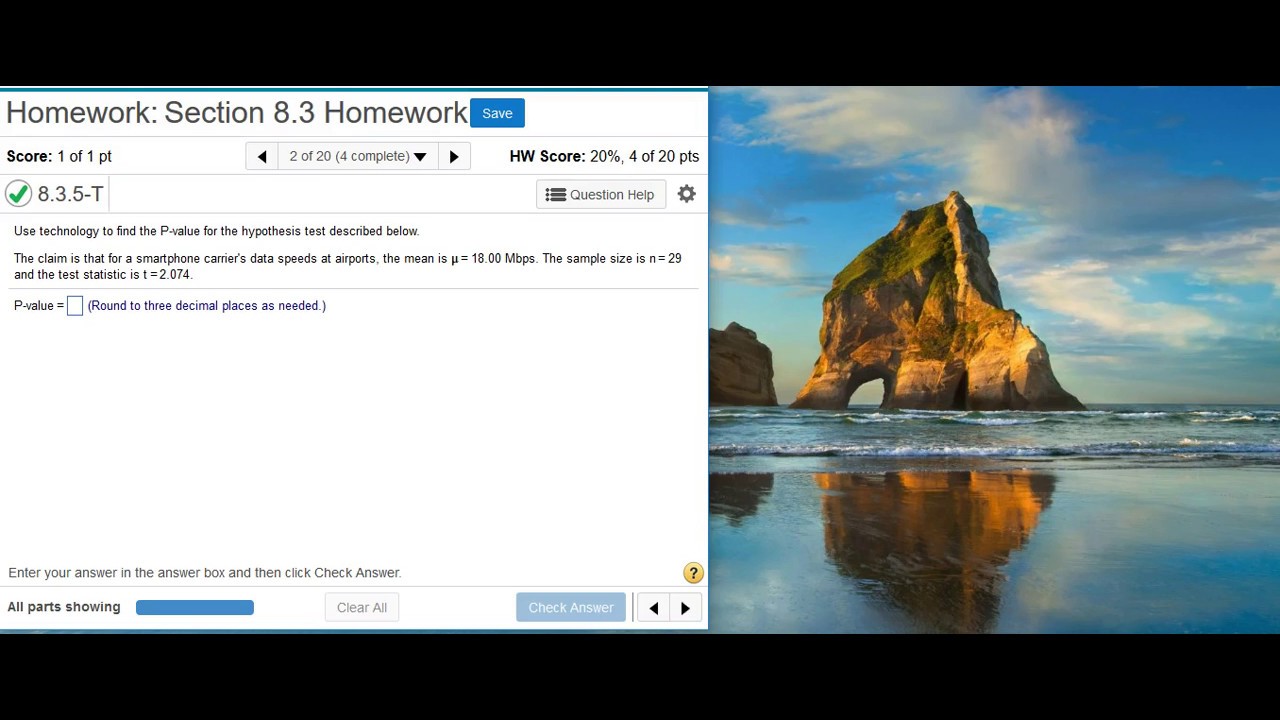
Finding a P-value given the test statistic

P Value and Hypothesis Testing Simplified|P-value and Hypothesis testing concepts in Statistics

Using a table to estimate P-value from t statistic | AP Statistics | Khan Academy

Takeaways

Q & A

What is Caterina's null hypothesis in the test?

What is the alternative hypothesis to Caterina's null hypothesis?

What sample size did Caterina use for her test?

What is the test statistic (T value) that Caterina obtained from her sample?

What is the formula for calculating the T value in Caterina's test?

What are the degrees of freedom in Caterina's test?

How does the T distribution differ from the Z distribution?

What does Caterina need to look up in the T table to find the P-value?

What is the approximate P-value for Caterina's test, according to the T table?

What does Caterina do with the P-value in relation to her significance level?

What does it mean if Caterina rejects the null hypothesis?

What does it imply if Caterina does not reject the null hypothesis?