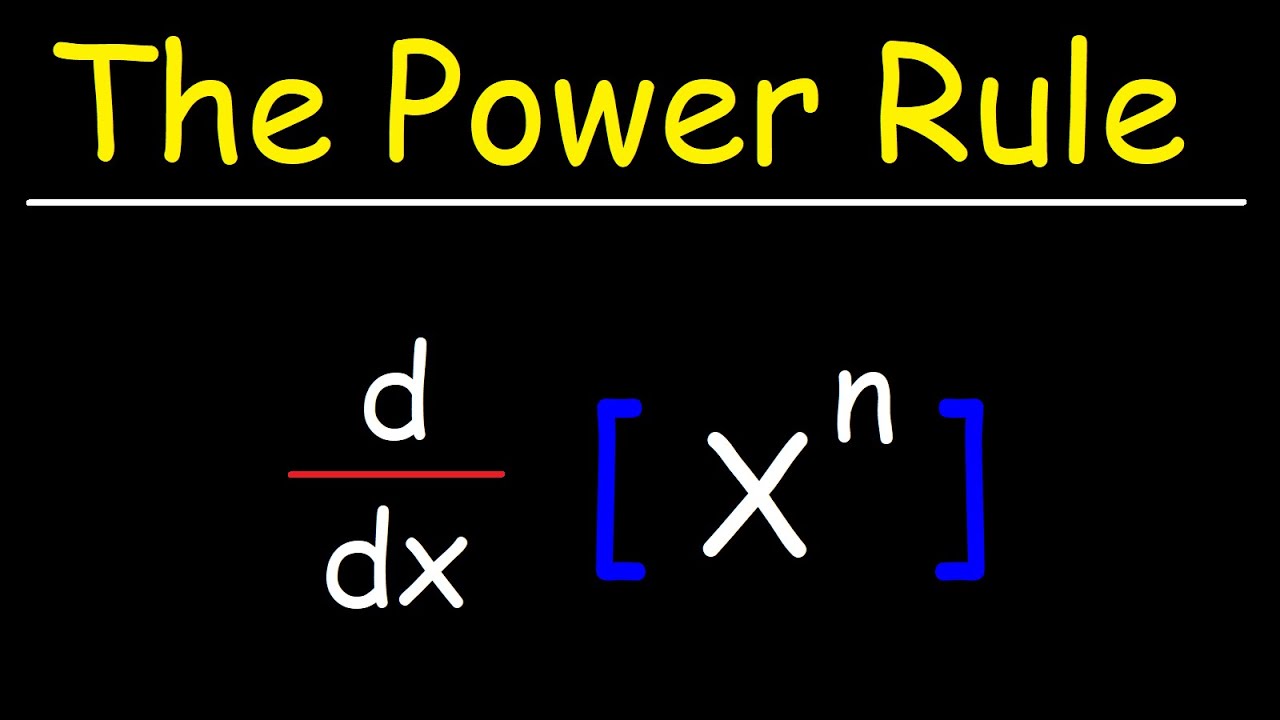Basic Derivative Rules - Part 1
TLDRThis video script introduces fundamental derivative rules, building upon the concept of derivatives as taught through the limit process in previous lessons. The focus is on shortcut methods for finding derivatives, starting with the power rule. The power rule states that for a function f(x) = x^n, the derivative f'(x) = n * x^(n-1). The script provides several examples to illustrate the application of the power rule, including handling negative exponents, rational exponents, and square roots. It also covers the derivative of a constant, which is always zero, and the sum and difference rule, which allows for the derivative to be found term by term. The constant multiple rule is also explained, emphasizing that the derivative of a constant times a function is the constant times the derivative of the function. The script concludes with a teaser for the next part of the lecture, which will involve combining these rules for more complex functions.
Takeaways
- 📚 The power rule states that the derivative of x to the power of n is n times x to the power of (n-1).
- 🔢 For negative exponents, the power rule still applies, and you subtract one from the exponent, resulting in a new negative exponent.
- 📉 Rational exponents, like fractions, are treated with the power rule by bringing the exponent down as a coefficient and reducing it by one.
- 🛑 When dealing with square roots or other radicals, first rewrite them as rational exponents before applying the power rule.
- ❌ Do not apply the power rule directly to expressions with variables in the denominator; rewrite them with the variable in the numerator.
- 🧮 The derivative of a constant is always zero, as constants do not change with respect to the variable.
- 🔁 The sum and difference rule allows you to find the derivative of a sum or difference of terms by finding the derivative of each term separately.
- 🆗 When applying the power rule to terms like x to the first power, the derivative simplifies to 1, since x^0 is 1.
- 📈 The constant multiple rule states that the derivative of a constant times a function is the constant times the derivative of the function.
- ✅ It's important to write the derivative in the same form as the original function, using the same types of expressions (e.g., radicals, negative exponents).
- 🔧 For more complex expressions, combining multiple rules is necessary, and it's helpful to break down the process into steps.
Q & A
What is the power rule for finding derivatives?
-The power rule states that if you have a function f(x) = x^n, then the derivative f'(x) is equal to n * x^(n-1). This means you take the exponent, bring it down as the coefficient of the variable, and reduce the exponent by one.
What is the derivative of x cubed according to the power rule?
-The derivative of x cubed (x^3) is 3x^2. You take the exponent 3, bring it down as the coefficient, and reduce the exponent by one to get 2.
How does the power rule apply to a function with a negative exponent?
-For a function with a negative exponent, like x^(-n), the power rule still applies. You bring the exponent down as the coefficient and reduce the exponent by one, being careful with the sign. For example, the derivative of x^(-7) would be -7x^(-8).
What is the process to handle a square root in the power rule?
-When you have a square root (a radical), you first rewrite it as a rational exponent, such as √x becoming x^(1/2). Then you apply the power rule by bringing down the exponent as a coefficient and reducing the exponent by one.
How should the derivative be written when the original function contains radicals?
-When the original function contains radicals, the derivative should also be written using radicals. It's a general rule to write the derivative in the same form as the original function for consistency and clarity.
What is the derivative of a constant function?
-The derivative of a constant function is always zero. This is because a constant does not change with respect to the variable, so its rate of change is zero.
How does the sum and difference rule apply when finding derivatives?
-The sum and difference rule states that for a function consisting of multiple terms added or subtracted, you find the derivative of each term separately and then add or subtract the results. For example, the derivative of x^3 + 2 is 3x^2, since the derivative of 2 (a constant) is zero.
What is the constant multiple rule in the context of derivatives?
-The constant multiple rule states that if you have a constant times a function, the derivative is simply the constant times the derivative of the function. For example, the derivative of -5x^2 is -5 times the derivative of x^2, which is -5 * 2x = -10x.
Why is the derivative of x to the first power just one?
-The derivative of x to the first power is one because when you apply the power rule, x^1 becomes 1 * x^(1-1), which simplifies to 1 * x^0. Since anything to the zero power is one, the derivative is just 1.
How should the final answer for a derivative be written if it contains negative exponents?
-It's generally preferred not to leave the final answer using negative exponents if it can be avoided. Instead, rewrite the expression to avoid negative exponents for a clearer presentation, unless the negative exponent is an inherent part of the function's form.
What is the next step after introducing the basic derivative rules in the video?
-The next step, as mentioned in the video, is to combine these basic derivative rules to solve more complex problems. The video script indicates that this will be covered in the second part of the lecture video.
Outlines
📚 Introduction to Derivative Rules
This paragraph introduces the concept of basic derivative rules as a shortcut method for finding derivatives, as opposed to using the limit process defined in previous lessons. The power rule is highlighted as the first among these shortcut rules, explaining that for a function f(x) = x^n, the derivative f'(x) = n * x^(n-1). The process involves taking the exponent as the coefficient and reducing the exponent by one. Several examples are provided to illustrate the application of the power rule, including cases with negative exponents, rational exponents, square roots, and variables in the denominator. The paragraph concludes with a note on the importance of writing derivatives in the same form as the original function, emphasizing the use of radicals and negative exponents where appropriate.
🔢 Derivative Rules for Constants, Sums, and Differences
The second paragraph delves into additional derivative rules, starting with the rule for constants, which states that the derivative of a constant function is always zero. The paragraph then covers the sum and difference rule, which allows for the derivative to be found term by term for functions that are sums or differences of multiple terms. Examples are provided to demonstrate the process, including a function with x cubed and a constant term, and another with x to the fifth power, x cubed, x, and a constant term. The constant multiple rule is also introduced, which states that the derivative of a constant times a function is simply the constant times the derivative of the function. An example is given to illustrate this, showing that the derivative of -5x is -5. The paragraph ends with a note on the application of the power rule to the first power, resulting in a derivative of one.
🔁 Combining Derivative Rules
The final paragraph announces the intention to combine the derivative rules discussed in the video. It mentions that to avoid making the video too long, the lecture will be broken into several parts. The speaker indicates that the next part of the lecture video will continue with the application of combining these rules for finding derivatives.
Mindmap
Keywords
💡Derivative
💡Power Rule
💡Exponent
💡Rational Exponent
💡Constant Function
💡Sum and Difference Rule
💡Constant Multiple Rule
💡Negative Exponent
💡Square Root
💡Variable in the Denominator
💡Combining Rules
Highlights
Introduction to basic derivative rules as shortcuts for finding derivatives.
Explanation of the power rule for functions of the form f(x) = x^n.
Derivative of x^n is n*x^(n-1), where the exponent becomes the coefficient and is reduced by one.
Example of applying the power rule to find the derivative of x^3, resulting in 3x^2.
Handling negative exponents in the power rule by adjusting the exponent accordingly.
Dealing with rational exponents by converting radicals to rational exponents before applying the power rule.
Rewriting expressions with variables in the denominator to apply the power rule.
General rule for writing derivatives in the same form as the original function.
Derivative of a constant function is always zero.
Sum and difference rule: derivatives are found term by term for sums and differences.
Example of finding the derivative of a sum of terms, such as 3x^2 for x^3 and 0 for the constant term.
Derivative of x to any power is 1 times the variable to the power of one less, using the power rule.
Constant multiple rule: the derivative of a constant times a function is the constant times the derivative of the function.
Example of applying the constant multiple rule to find the derivative of -5x^2 as -5.
Combining multiple rules for more complex derivative calculations.
Breaking down the lecture into several parts to avoid overwhelming length.
Continuation of the lecture in a second part focusing on combining rules.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: