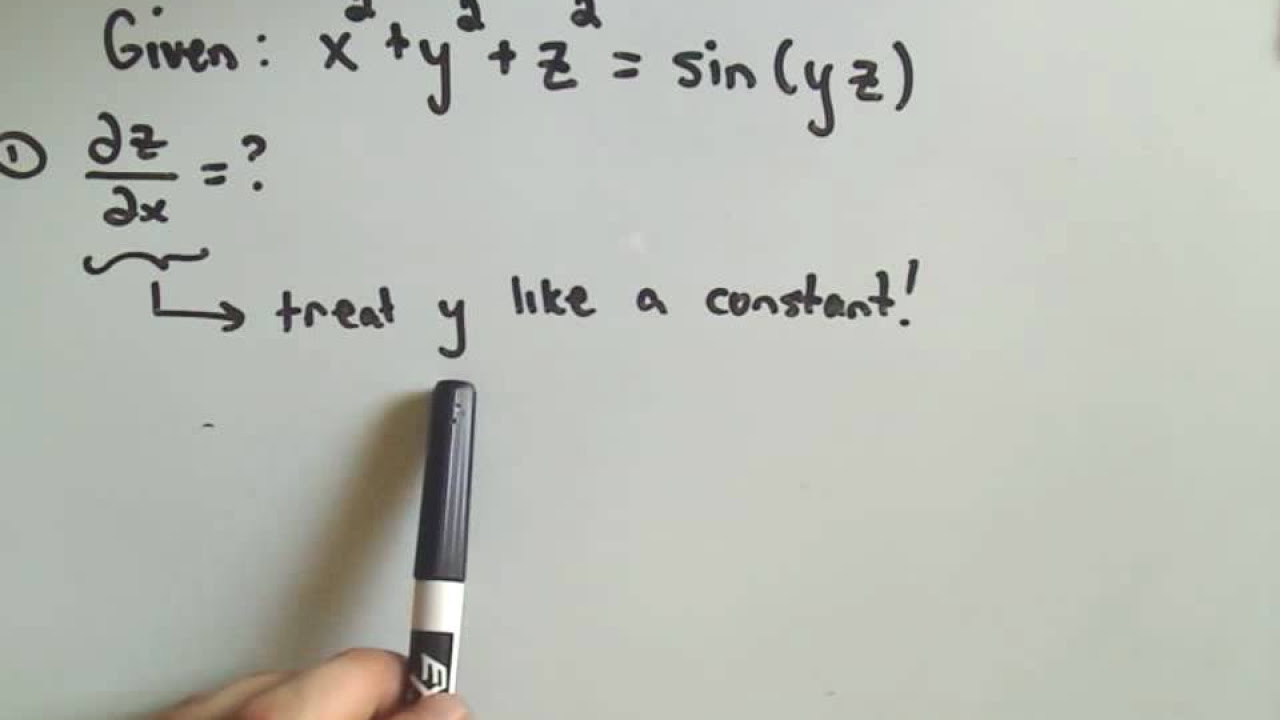Partial Derivatives - Multivariable Calculus
TLDRThis video script offers a comprehensive guide on finding partial derivatives of multivariable functions. It begins by illustrating how to calculate the partial derivative with respect to a specific variable, treating all other variables as constants. The script then reviews the power rule for differentiation and applies it to progressively complex functions involving variables x and y. The concept of the derivative of exponential functions is also covered, highlighting the use of the chain rule. The video further explores the partial derivatives with respect to different variables in functions, emphasizing the need to treat the non-differentiated variables as constants. Several examples are provided to solidify the concept, including the differentiation of natural logarithm functions and the application of the product and quotient rules where necessary. The script concludes with a discussion on higher-order partial derivatives, showcasing the process of finding second and third order derivatives, and introducing the important theorem of equality of mixed partial derivatives. This theorem states that for a continuous function, the order of differentiation does not affect the result, proving that mixed partial derivatives are equal if each variable is differentiated the same number of times.
Takeaways
- 📘 To find the partial derivative of a function with multiple variables, treat all other variables as constants except for the one with respect to which you are differentiating.
- 📙 The power rule for differentiation states that the derivative of x to the power of n is n times x to the power of (n - 1).
- 📕 When differentiating an exponential function, use the formula (e^u) * (du/dx), where u is the exponent and (du/dx) is the derivative of the exponent.
- 📖 For natural logarithm functions, the derivative is given by (1/u) * (du/dx), where u is the argument of the logarithm.
- 📔 The product rule for differentiation is necessary when differentiating a product of two functions, and it states that (d/dx)(fg) = f'g + fg'.
- 📒 The quotient rule is applied when differentiating a quotient of two functions, expressed as (f'g - fg') / g^2.
- 📓 Chain rule is used when differentiating composite functions, bringing down the outer function and differentiating the inner function.
- 📔 For second and higher order partial derivatives, the order of differentiation does not matter if the function is continuous, a property known as Clairaut's theorem.
- 📘 When evaluating a derivative at a specific point, substitute the point's coordinates into the derivative to find the rate of change at that point.
- 📙 Mixed partial derivatives of the same order, involving different variables, are equal if the function is continuous, which is a consequence of Clairaut's theorem.
- 📗 Practice is essential for mastering the concept of partial derivatives, and trying out different problems helps solidify understanding.
Q & A
What is the symbol used to represent the partial derivative of a function with respect to x?
-The partial derivative of a function with respect to x is symbolized by f_x or ∂f/∂x.
When finding the partial derivative with respect to x, how should you treat the other variables in the function?
-When finding the partial derivative with respect to x, you should treat all other variables as constants.
What is the power rule for differentiation?
-The power rule states that the derivative of x to the power of n (x^n) is n times x to the power of n minus one (n * x^(n-1)).
How do you find the first partial derivative of a function with respect to x if the function is e^(x^2 * y^3)?
-To find the first partial derivative with respect to x, you would treat y as a constant and differentiate e^(x^2 * y^3) with respect to x, which results in 2x * y^3 * e^(x^2 * y^3).
What is the process for finding the partial derivative with respect to y of a function?
-To find the partial derivative with respect to y, you would treat x as a constant and differentiate only the terms involving y.
What is the derivative of a constant with respect to a variable?
-The derivative of a constant with respect to any variable is zero because a constant does not change with respect to any variable.
What is the natural log function's derivative with respect to its argument?
-The derivative of the natural log function ln(u) with respect to its argument is u'/u, where u' is the derivative of the argument with respect to the variable.
How can you find the slope of a surface at a given point in a multivariable function?
-To find the slope of a surface at a given point in a multivariable function, you find the partial derivatives with respect to each variable (e.g., fx and fy) and evaluate them at the given point.
What is the product rule used for in differentiation and how is it expressed?
-The product rule is used when differentiating a product of two functions. It is expressed as (f * g)' = f' * g + f * g', where f and g are functions and f' and g' are their respective derivatives.
When is the quotient rule necessary for differentiation?
-The quotient rule is necessary when differentiating a quotient of two functions where both the numerator and the denominator contain the variable with respect to which you are differentiating.
What does the equality of mixed partial derivatives theorem state?
-The equality of mixed partial derivatives theorem states that for a continuous function, the mixed partial derivatives are equal, meaning that f_xy is equal to f_yx, regardless of the order in which the differentiation is performed.
Outlines
🤓 Introduction to Partial Derivatives
This paragraph introduces the concept of partial derivatives, explaining how to find the partial derivative of a function with multiple variables, such as x and y. It uses the function f(x, y) = 7x^2 - x^3y^4 + 5x^4y^3 as an example and demonstrates treating all variables except the one with respect to which we are differentiating as constants. The power rule for differentiation is also reviewed, and the partial derivatives with respect to x and y are calculated for the given function.
📚 Applying the Power and Product Rules
The paragraph demonstrates the process of finding partial derivatives with respect to x and y for two different functions. The first function is z = 3x^2y^4 - 5x^7 + 4y^8, and the second is z = x^4e^(y^5). The power rule is applied to find the derivatives, and the product rule is introduced for cases where the derivative involves a product of two functions. The paragraph also provides an example of finding partial derivatives for an exponential function.
🔍 Derivatives of Natural Logarithm Functions
This section focuses on differentiating functions involving natural logarithms. It explains the derivative of ln(u) as u'/u and applies this to functions such as ln(x^2 + y^2). The paragraph provides a method to find the partial derivatives with respect to x and y for a given function and includes an example where the derivative involves the natural logarithm of a quotient of x and y.
🔢 Partial Derivatives of Trigonometric and Square Root Functions
The paragraph explores finding partial derivatives for functions involving trigonometric and square root expressions. It covers how to differentiate sine functions and square roots, using the chain rule as necessary. Examples include finding partial derivatives for z = sin(x^3y^5) and f(x, y) = √(x^2 + y^2), as well as a trigonometric function involving x and y.
📈 Evaluating Partial Derivatives at Specific Points
This part of the script discusses how to evaluate partial derivatives at specific points, such as (1,2). It involves finding the partial derivatives with respect to x and y for a given function and then substituting the coordinates of the point into these derivatives to find their values. An example is provided to illustrate the process.
🤔 When to Use the Product Rule
The paragraph clarifies when to use the product rule in differentiation. It emphasizes that the product rule is necessary when differentiating a product of two functions, both of which contain the variable with respect to which differentiation is being performed. Examples are given to illustrate the use of the product rule in finding partial derivatives with respect to x and y.
🧮 Quotient Rule in Partial Derivatives
This section explains the use of the quotient rule in finding partial derivatives. It states that the quotient rule is applicable when differentiating a quotient of two functions, both of which contain the variable with respect to which differentiation is being performed. The paragraph provides an example function and shows how to find its partial derivatives with respect to x and y, using the quotient rule where necessary.
📊 Partial Derivatives in Three Variables
The paragraph extends the concept of partial derivatives to functions of three variables, such as f(x, y, z). It explains how to find the partial derivatives with respect to each variable, treating the other variables as constants. An example function is provided, and its partial derivatives with respect to x, y, and z are calculated.
🧲 Mixed Partial Derivatives and Their Equality
This section delves into mixed partial derivatives, which are derivatives taken with respect to different variables in a different order. It presents a theorem stating that if a function is continuous, then its mixed partial derivatives are equal, meaning that f_xy is equal to f_yx, and so on. The paragraph provides examples to demonstrate the calculation and equality of mixed partial derivatives for different orders of differentiation.
🔁 Proving Equality of Mixed Partial Derivatives
The final paragraph provides a detailed proof to demonstrate the equality of mixed partial derivatives for a given function. It shows through calculation that f_xy equals f_yx, and extends this to higher-order derivatives, proving that the order of differentiation does not affect the result as long as each variable is differentiated the same number of times. This reinforces the concept that mixed partial derivatives are the same if the function is continuous and the number of differentiations with respect to each variable is equal.
Mindmap
Keywords
💡Partial Derivative
💡Power Rule
💡Constants
💡Product Rule
💡Chain Rule
💡Exponential Function
💡Natural Log Function
💡Quotient Rule
💡Trigonometric Functions
💡Second and Higher Order Partial Derivatives
💡Equality of Mixed Partial Derivatives
Highlights
Introduction to finding partial derivatives with respect to a certain variable in a multivariable function.
Explanation of treating all other variables as constants when finding the partial derivative with respect to one variable.
Review of the power rule for differentiation and its application to partial derivatives.
Process of finding the first partial derivative with respect to x of a given function.
Derivation of the partial derivative with respect to y, treating x as a constant.
Application of the power rule to find the partial derivatives of a function with exponential terms.
Differentiation of a function involving natural logarithms and the use of the chain rule.
Evaluation of partial derivatives at a given point by substituting the coordinates into the derivative.
Use of the product rule in partial differentiation when the variable appears in both parts of the function.
Differentiation of a function with three variables and finding the first three partial derivatives.
Process of finding higher order partial derivatives and the concept of mixed partial derivatives.
Proof of the equality of mixed partial derivatives using a specific function as an example.
Explanation of the conditions under which mixed partial derivatives are equal and the importance of the function being continuous.
Differentiation of a function with respect to three different variables to find a mixed third order derivative.
Demonstration of the process to find all four second partial derivatives of a function with two variables.
Use of the quotient rule in partial differentiation when differentiating a function with variables in both the numerator and the denominator.
Differentiation of a function involving square roots and trigonometric functions, showcasing the application of various differentiation rules.
Final summary reinforcing the understanding of partial derivatives, their calculation, and the conditions for equality of mixed partials.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: