Calculus Worksheet
TLDRThe provided transcript is a comprehensive lecture on derivatives, covering a range of mathematical functions and their successive derivatives. The speaker begins by explaining the power rule for derivatives and demonstrates its application to various functions, including polynomials and trigonometric functions. The lecture progresses to discuss the derivative of exponential functions, the use of the chain rule, and the quotient rule. It also touches on the pattern of derivatives for functions like y = 2/x, highlighting the alternating signs and the involvement of factorials in the nth derivative. The speaker provides step-by-step solutions to find the first, second, third, and fourth derivatives of given functions, offering insights into the process and the mathematical reasoning behind each step. The summary concludes with the identification of a general pattern for the nth derivative of y = 2/x, which involves an alternating sequence and factorials, and confirms the pattern's accuracy by applying it to find a specific derivative.
Takeaways
- 📚 The power rule for derivatives states that if y = ax^n, then the derivative dy/dx = n*a*x^(n-1).
- 🔄 To find higher order derivatives, apply the power rule iteratively, reducing the exponent by one each time.
- ✅ When dealing with fractions, rewrite them as a single term with positive exponents before differentiating.
- 📐 For trigonometric functions, remember that the derivative of cosine is -sine and the derivative of sine is cosine.
- 🔢 For exponential functions involving e^u, use the chain rule, where the derivative of e^u is e^u times the derivative of u.
- 📈 The product rule is essential for finding derivatives of functions that are a product of two other functions, such as x * sin(x).
- 📉 The quotient rule is used for finding derivatives of functions that are one function divided by another, such as x / (x + 1).
- 🔁 The pattern for the nth derivative of y = 2/x is given by (-1)^n * 2 * n! / x^(n+1), which involves alternating signs and factorials.
- 🧮 For polynomial functions, the nth derivative will eventually reach a constant value and then become zero after one more derivative.
- 🤔 Memorization of trigonometric and exponential derivatives is crucial for efficiently solving derivative problems.
- 📌 Always check the pattern of derivatives as you progress to higher orders to identify any repeating or terminating behavior.
Q & A
What is the power rule for derivatives?
-The power rule states that if you have a function y = ax^n, the derivative of y with respect to x is found by bringing the exponent down in front, multiplying by the coefficient (a), and then subtracting one from the exponent. So, the derivative dy/dx = n * a * x^(n-1).
How do you find the third derivative of a function written as a fraction?
-First, rewrite the function with the terms on the bottom as having positive exponents on the top. Then, apply the power rule to find each successive derivative, remembering to subtract one from the exponent each time. Finally, if needed, convert back to fractional form by inverting the terms with positive exponents.
What is the derivative of cosine of x?
-The derivative of the cosine function, cos(x), with respect to x is the negative sine function, -sin(x).
How do you find the second derivative of an exponential function like e^(6x)?
-For an exponential function e^(ax), the first derivative is found by multiplying the original function by 'a', resulting in a * e^(ax). The second derivative is found by multiplying the first derivative by 'a' again, resulting in a^2 * e^(ax).
What is the product rule for derivatives?
-The product rule states that if you have a function y = f(x) * g(x), the derivative of y with respect to x is found by taking the derivative of the first function times the second function plus the first function times the derivative of the second function. Mathematically, dy/dx = f'(x) * g(x) + f(x) * g'(x).
How do you find the nth derivative of a function?
-To find the nth derivative of a function, you apply the derivative operation n times. Each application of the derivative operation will simplify the function according to the rules of differentiation, such as the power rule, product rule, chain rule, or trigonometric function derivatives, until you reach the nth derivative.
What is the quotient rule for derivatives?
-The quotient rule states that if you have a function y = f(x) / g(x), the derivative of y with respect to x is found by taking the derivative of the numerator times the denominator, minus the numerator times the derivative of the denominator, all divided by the square of the denominator. Mathematically, dy/dx = [g(x) * f'(x) - f(x) * g'(x)] / [g(x)]^2.
What is the derivative of the natural logarithm of x, ln(x)?
-The derivative of the natural logarithm function, ln(x), with respect to x is 1/x.
How do you determine the pattern for the nth derivative of a function?
-To determine the pattern for the nth derivative, you can calculate the first few derivatives and look for a repeating pattern or rule. This might involve recognizing alternating signs, factorials, or powers of constants, and then formulating a general expression that can be applied to find any nth derivative.
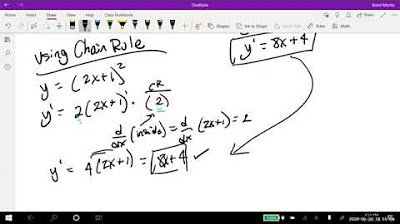
What is the chain rule for derivatives?
-The chain rule states that the derivative of a composite function, f(g(x)), is found by multiplying the derivative of the outer function evaluated at the inner function, f'(g(x)), by the derivative of the inner function, g'(x). Mathematically, (f(g(x)))' = f'(g(x)) * g'(x).
How do you find the second derivative of a function involving a trigonometric function like tan(x)?
-To find the second derivative of a trigonometric function like tan(x), you first find the first derivative, which involves recognizing the derivative of tan(x) as sec^2(x). Then, apply the chain rule to find the second derivative, which will involve the derivatives of secant and tangent functions.
Outlines
📚 Introduction to Derivatives and Power Rule
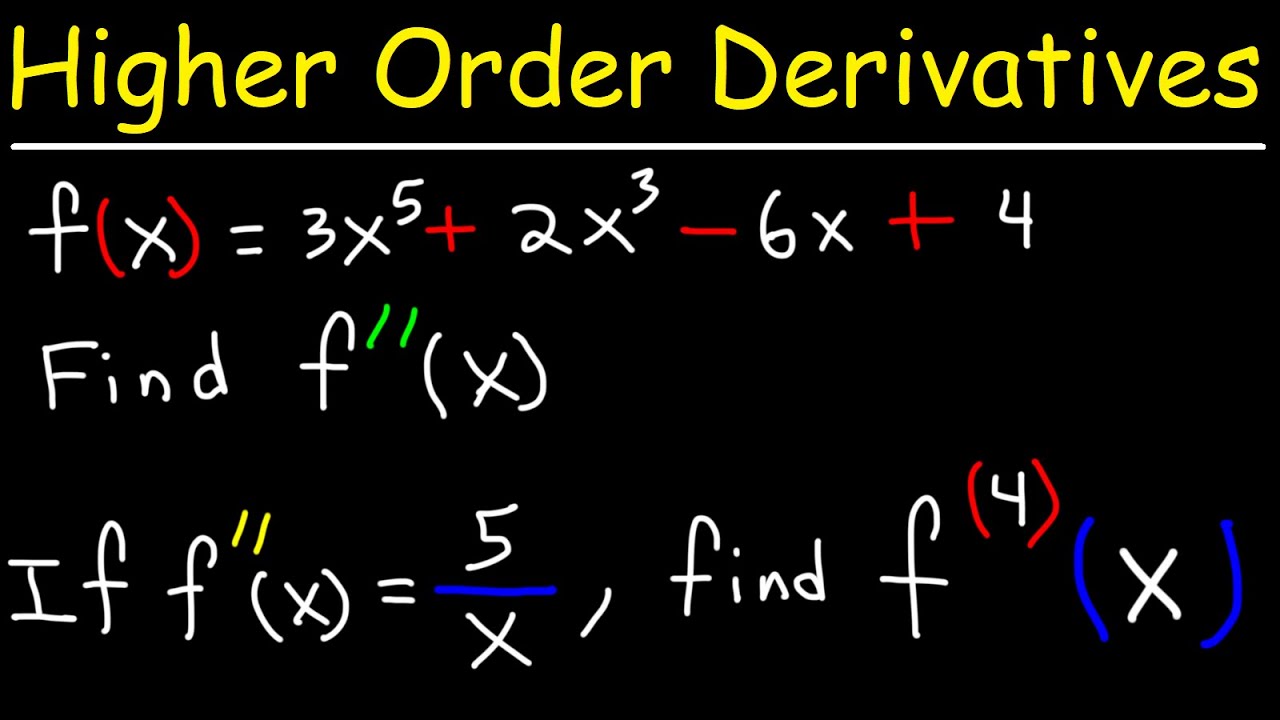
This paragraph introduces the concept of derivatives and explains the power rule for finding the derivatives of functions. The power rule states that for a function y = ax^n, the derivative is found by bringing the exponent down in front, multiplying by the coefficient (a), and then subtracting one from the exponent. The paragraph demonstrates the process of finding the first and second derivatives of a function y = 3x^7 + 2x^5 - 18x^2 + 1, and the third derivative of y = 2x^-2 - 4x^-1. It also covers the process of rewriting fractions as whole expressions before differentiating.
🔍 Derivatives of Trigonometric and Exponential Functions
The second paragraph delves into finding derivatives of more complex functions, including those involving trigonometric and exponential components. It covers the derivatives of y = 4cos(x), where the derivative of cosine is -sin(x), and the subsequent derivatives follow a pattern of alternating signs. The paragraph also discusses the derivatives of y = e^(6x), explaining the use of the chain rule for exponential functions and how to apply it to find the second derivative. Lastly, it touches on the derivatives of a polynomial function, f(x) = 8x^3 - sin(x), and how to find up to the fourth derivative using the power rule and recognizing that the derivative of a constant is zero.
🧮 Product, Chain, and Quotient Rule Applications
This paragraph explores the application of the product rule, chain rule, and quotient rule in finding derivatives. It starts with the product rule for the function y = x*sin(x), illustrating how to multiply the first function by the derivative of the second and add it to the second function times the derivative of the first. The chain rule is applied to the function f(x) = 3x + 4^5, showing how to bring down the exponent and multiply by the derivative inside. The quotient rule is demonstrated for the function f(x) = x/(x+1), explaining how to derive the expression by multiplying the bottom function by the derivative of the top and subtracting the top function times the derivative of the bottom, all over the bottom squared. The paragraph concludes with a question about the nth derivative of x until it equals zero, explaining that the nth derivative will be zero when n is one more than the highest power of x in the original function.
🔢 Derivatives of Logarithmic and Sine Functions
The fourth paragraph focuses on the derivatives of logarithmic and sine functions. It begins with the derivative of y = ln(3x), using the property of logarithms that the derivative of ln(u) is 1/u * du/dx. The paragraph then finds the first, second, and third derivatives of this function, demonstrating the use of power rule for negative exponents. It proceeds to find the fourth derivative of y = sin(6x) - 3, showing the pattern of derivatives of sine and cosine functions and how they alternate in sign. The paragraph concludes with a formula for the nth derivative of y = 2/x, which is derived through observation and application of factorials.
🔁 Pattern Recognition in Derivatives
The final paragraph investigates the pattern in the derivatives of the function y = 2/x. It begins by calculating the first few derivatives and observing an alternating sign pattern that involves factorials. The paragraph derives a general formula for the nth derivative of y = 2/x, which is given by (-1)^(n-1) * 2 * n! / x^(n+1). The formula is then tested for the third derivative to confirm its accuracy. The paragraph concludes with an invitation for viewers to ask questions via email if they have any.
Mindmap
Keywords
💡Derivative
💡Power Rule
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Trigonometric Derivatives
💡Exponential Functions
💡Second Derivative
💡Third Derivative
💡nth Derivative
💡Factorials
Highlights
The power rule for derivatives is explained, where the exponent is brought down and one is subtracted from it.
The process of finding the second derivative of a function by applying the power rule twice is demonstrated.
Rewriting expressions with fractions as a sum or difference before differentiating is suggested for clarity.
The derivatives of trigonometric functions, specifically cosine and sine, are discussed with examples.
The use of the chain rule and the derivative of e to the power of x is explained.
The derivative of a product of functions is found using the product rule, demonstrated with an example involving sine of x.
The quotient rule is applied to find the derivatives of a rational function, such as x over (x + 1).
The pattern for the nth derivative of y equals 2 over X is derived using factorials and alternating signs.
The nth derivative of x to the power of n is discussed, showing that it equals zero after a certain point.
The application of the chain rule to find higher order derivatives of composite functions is shown.
The use of the power rule for derivatives of functions involving x to the power of a constant is demonstrated.
The importance of memorizing the derivatives of basic trigonometric functions for solving complex problems is emphasized.
The method for finding the nth derivative of a function using a formula involving factorials and alternating signs is presented.
The process of finding the nth derivative of a function by applying the power rule iteratively is shown.
The pattern of derivatives for a function involving the natural logarithm is discussed, highlighting the use of the reciprocal function.
The concept of the nth derivative of a polynomial function eventually becoming a constant and then zero is explained.
The transcript provides a comprehensive guide on finding derivatives of various types of functions using different mathematical rules.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: