Physics 15 Torque (2 of 27) Find the Angle (No Torque)

Michel van Biezen
10 Jan 201606:29
EducationalLearning
32 Likes 10 Comments

TLDRIn this online lecture, the presenter explores a physics problem involving a suspended object supported by a rope over two pulleys with heavy weights at each end. The focus is on finding the angle of suspension when a 1000 Newton force is applied in the middle, with 2000 Newtons on either end. Using trigonometric principles, the tension in the rope is broken down into horizontal and vertical components, which are then used to set up equations for force balance. The problem is solved algebraically, revealing that the angle can be reduced by increasing the weight at the ends. However, it is shown that as the angle approaches zero, the required weight approaches infinity, indicating that it's impossible to achieve a perfectly horizontal position with finite mass. This engaging problem illustrates the limits of mechanical equilibrium and the role of trigonometry in physics.

Takeaways
  • 📐 **Force Equilibrium**: The sum of forces in the x-direction and y-direction must add up to zero for the system to be in balance.
  • 🧵 **Tension Division**: The tension in the rope is divided into vertical and horizontal components, with symmetry meaning both sides have equal magnitudes of tension.
  • 🔢 **Force Components**: The horizontal component of tension (T_x) is calculated as T times the cosine of the angle, while the vertical component (T_y) is T times the sine of the angle.
  • ⚖️ **Equilibrium Equation**: The equation for equilibrium in the y-direction is 2 * T_y - mg = 0, where mg is the weight of the object.
  • 🎛️ **Tension Calculation**: Given a weight of 2000 Newtons on either side, the tension T in the rope is also 2000 Newtons.
  • 🧮 **Solving for Angle**: To find the angle (theta), use the equilibrium equation and solve for the sine of theta, which gives the angle as the arc sine of (1000 / 4000).
  • 📐 **Angle Calculation**: The calculated angle is approximately 14.5 degrees, which is derived from the sine of theta being 1/4.
  • ∞ **Theoretical Limit**: To reduce the angle to zero, theoretically, an infinite amount of weight would be required on both ends of the rope.
  • 💡 **Practical Limitation**: In practice, it's impossible to have an infinite amount of weight, so the angle can never be reduced to zero; there will always be some angle present.
  • 🔍 **Component Cancellation**: The horizontal components of tension cancel each other out due to symmetry, which is key to solving the problem.
  • 📉 **Increasing Weight**: To decrease the angle and move towards a more horizontal position, more weight must be added to the ends of the rope.
Q & A

  • What is the main concept being discussed in the lecture?

    -The lecture discusses the concept of equilibrium in a mechanical system where an object is suspended by a rope over two pulleys with weights on either end.

  • What are the conditions for equilibrium in the system described?

    -For the system to be in equilibrium, the sum of the forces in the x-direction and the sum of the forces in the y-direction must both add up to zero.

  • How is the tension in the rope divided into components?

    -The tension in the rope is divided into vertical and horizontal components, denoted as T_x and T_y respectively, which are calculated using the cosine and sine of the angle theta.

  • What is the relationship between the angle theta and the forces acting on the system?

    -The angle theta is related to the forces through the equation that the sum of the vertical forces (T_y) minus the gravitational force (mg) equals zero.

  • What is the significance of the symmetry in the system?

    -Due to symmetry, the horizontal components of tension (T_x) on both sides are equal in magnitude and cancel each other out, simplifying the force analysis.

  • How is the angle theta calculated in the given example?

    -Theta is calculated by setting up the equilibrium equation for the y-direction, substituting the known values, and solving for theta, which is found to be the arc sine of 1/4 or 14.5 degrees.

  • What happens to the required weight (mg) on the ends of the strings as the angle theta approaches zero?

    -As theta approaches zero, the required weight (mg) increases and tends towards infinity, indicating that an infinite amount of weight would be needed to make the angle zero and the system perfectly horizontal.

  • Why is it impossible to have a perfectly horizontal system with finite weights?

    -It is impossible because as the angle approaches zero, the denominator in the equation mg = 1000N / sin(theta) approaches zero, which would require an infinite value of mg to maintain equilibrium.

  • What is the role of the 1000 Newtons hanging from the string in the middle?

    -The 1000 Newtons hanging from the string in the middle represents the force that needs to be balanced by the weights on either end of the system, contributing to the equilibrium condition.

  • How does the tension in the string relate to the weights on either end?

    -The tension in the string is equal to the weight of the heaviest object in the system, which in this case is 2000 Newtons on either end, due to the balance of forces required for equilibrium.

  • What is the implication of the problem for real-world applications?

    -The problem illustrates the principles of force balance and equilibrium that are crucial in designing mechanical systems such as pulleys, cranes, and suspensions, where precise force distribution is necessary.

  • How can one visualize the forces acting on the system?

    -One can visualize the forces by drawing a free body diagram of the system, showing all the forces acting on the object, including the tensions in the rope and the gravitational forces, and then applying the equilibrium conditions.

Outlines
00:00
🔍 Analyzing the Suspension System with Forces

This paragraph discusses an interesting example of a suspension system where an object is held in balance by a rope over two pulleys with heavy weights on either end. The key focus is on finding the angle at which the system is in equilibrium. The problem is approached by applying the equations of force in the x-direction and y-direction, ensuring they sum up to zero. The tension in the rope is divided into vertical and horizontal components, and the forces are analyzed at a specific point. The tension is then related to the sine and cosine of the angle theta. Using the equilibrium condition, an equation is set up to solve for the angle theta. The tension in the rope is found to be 2000 Newtons, and the angle is calculated to be 14.5 degrees using the arcsine function.

05:02
📉 The Effect of Weight on the Angle

This paragraph explores how the angle of the suspension system changes with varying weights. It is shown that as the angle approaches zero, the required weight on the ends of the rope approaches infinity. This is because the weight is in the denominator of the equation relating weight to the sine of the angle. The limit of the weight as the angle approaches zero is infinite, indicating that it is impossible to have a perfectly horizontal position without an infinite amount of weight. The conclusion is that there will always be some angle present unless an infinite amount of weight is added to lift the object to a completely horizontal position.

Mindmap
Keywords
💡Torque
Torque is the rotational equivalent of linear force and is a measure of the force that can cause an object to rotate around an axis. In the context of the video, torque is not directly applied but is an important concept when considering the forces acting on the system. The script implies that the system is in equilibrium, meaning the net torque around any point is zero.
💡Force
Force is a physical quantity that represents the interaction between objects and can cause a change in the motion of an object. In the video, the forces are broken down into components acting in the x and y directions to analyze the equilibrium of the system. The script discusses how the sum of forces in both directions must equal zero for the object to be suspended in balance.
💡Equilibrium
Equilibrium refers to a state in which all forces acting on an object are balanced, resulting in no net force and no acceleration. The video's main theme revolves around finding the conditions for equilibrium in a mechanical system involving pulleys and weights. The script uses the concept of equilibrium to derive the angle at which the system is balanced.
💡Pulleys
Pulleys are mechanical devices that facilitate the lifting of weights by changing the direction of the force applied. In the script, pulleys are used to suspend an object with ropes, allowing for the distribution of forces in a way that maintains balance. The system's configuration with pulleys is central to the problem-solving process described in the video.
💡Weights
Weights are objects with mass that are used to apply force through gravity. In the video, weights are attached to the ends of the ropes to balance the system. The script discusses how the magnitude of these weights and their distribution affect the angles formed by the ropes and the equilibrium of the system.
💡Tension
Tension is the force experienced by a rope or cable when it is pulled tight by opposing forces. In the context of the video, tension in the ropes is critical for maintaining the balance of the suspended object. The script explains how the tension is resolved into horizontal and vertical components to satisfy the equilibrium conditions.
💡Components
Components refer to the individual parts of a vector that are resolved along the axes of a coordinate system. The script describes how the tension in the ropes is divided into horizontal (x-direction) and vertical (y-direction) components. These components are essential for applying the equilibrium equations to solve for the unknowns in the system.
💡Symmetry
Symmetry in this context refers to the balanced and identical arrangement of forces or components in a system. The script mentions symmetry when discussing the tension in the ropes, which allows for the cancellation of horizontal components and simplifies the calculation of forces in the y-direction.
💡Angle Theta
Angle Theta (θ) is the angle formed between the rope and the horizontal direction. The video's problem involves finding the value of this angle for given forces. The script uses trigonometric relationships to express the horizontal and vertical components of tension in terms of this angle and solve for its value.
💡Trigonometric Functions
Trigonometric functions, such as sine and cosine, are used to relate the angles of a triangle to the ratios of its sides. In the video, these functions are used to express the components of tension in the ropes in terms of the angle theta. The script applies the cosine and sine functions to find the horizontal and vertical components of tension, respectively.
💡Arc Sine
The arc sine (sin^(-1)) is the inverse function of the sine and is used to find the angle when the sine value is known. In the script, the arc sine is used to calculate the angle theta after determining the sine of theta from the equilibrium equation. It is a key step in solving for the angle that allows the system to be in balance.
💡Limit
In mathematics, a limit is a value that a function or sequence approaches as the input approaches some value. The script discusses the concept of a limit when considering the scenario where the angle theta approaches zero. It is used to illustrate that an infinite amount of weight would be required to achieve a perfectly horizontal position, which is theoretically impossible.
Highlights

The lecture discusses an interesting example of a suspended object with ropes over two pulleys and heavy weights on either end to balance it.

The forces in the x-direction and y-direction must add up to zero for the object to be in equilibrium.

The tension in the string is equal to the weight of the object hanging from it.

The tension can be divided into vertical and horizontal components using trigonometry.

The horizontal tension components cancel each other out due to symmetry.

The vertical tension components add up to zero in equilibrium.

The horizontal tension T_x is equal to T times the cosine of the angle theta.

The vertical tension T_y is equal to T times the sine of the angle theta.

The sum of all forces in the y-direction must add up to zero for equilibrium.

Solving for the angle theta gives the equilibrium angle of the ropes.

Increasing the weight on the ends decreases the angle, but an infinite amount of weight is needed to make the angle zero.

The lecture demonstrates the relationship between the weight and the sine of the angle using trigonometry.

As the angle approaches zero, the required weight approaches infinity.

It is impossible to have a perfectly horizontal rope without an infinite amount of weight.

The lecture provides a practical application of trigonometry and physics to solve real-world problems.

The problem illustrates the limits of physical systems and the importance of considering theoretical limits.

The lecture is a valuable resource for students studying physics and engineering.

The problem-solving approach used in the lecture can be applied to a wide range of engineering problems.

Transcripts

Browse More Related Video

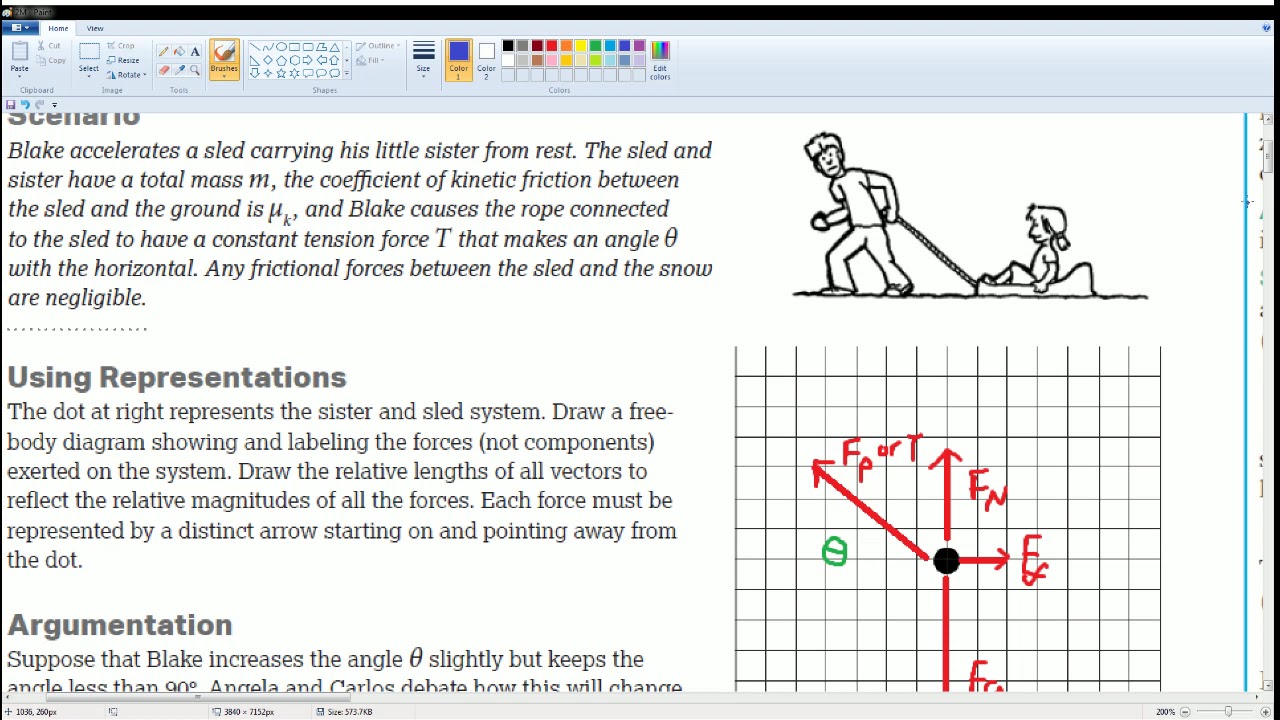
AP Physics Workbook 2.M Limiting Cases

Physics 15 Torque (3 of 27) Tension=? in the Cable

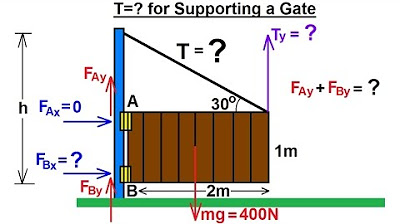
Physics 15 Torque (5 of 27) Tension=? Supporting a Gate

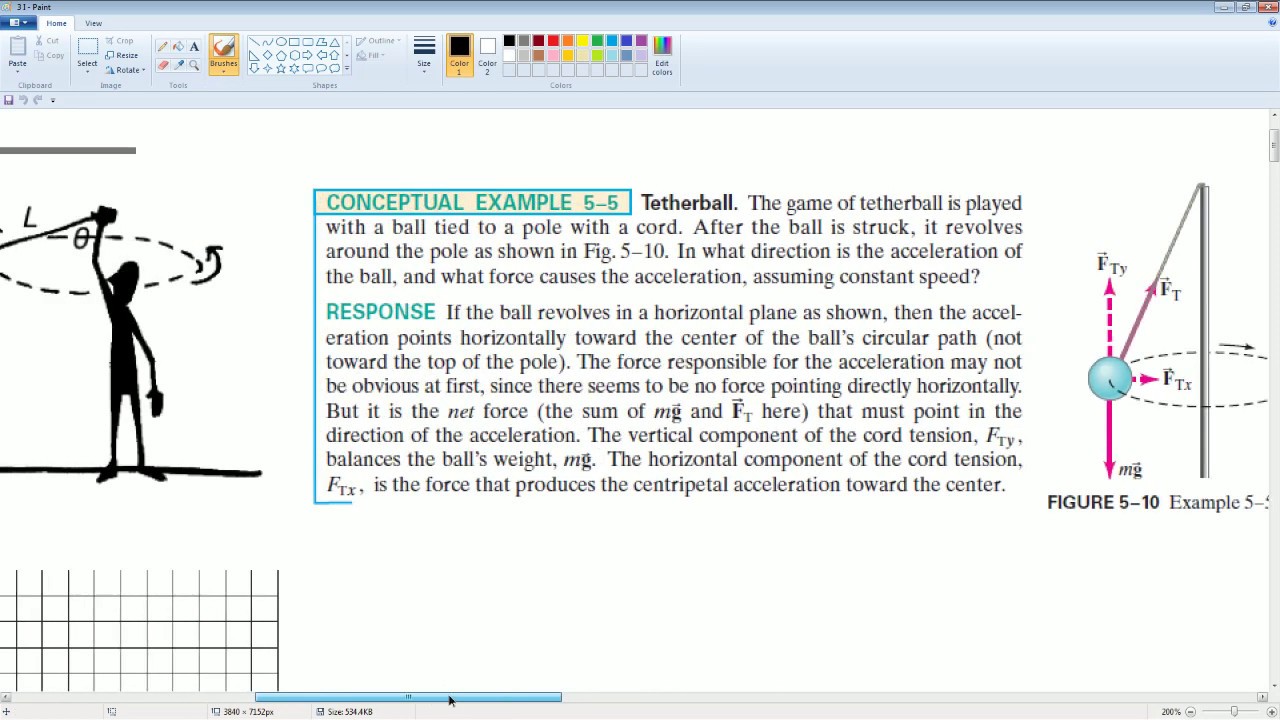
AP Physics Workbook 3.I The Conical Pendulum

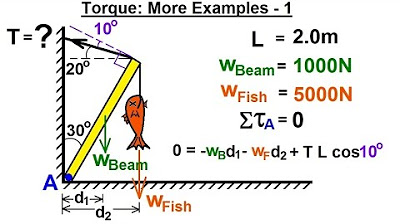
Physics 15 Torque (19 of 25) More Examples: 1 T=? of Cable Holding Fish

Physics 15 Torque Fundamentals (8 of 13) How to Calculate a Torque (Basic Example 2)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEquilibriumTensionLectureForce AnalysisEngineeringEducationalProblem SolvingPulleysWeight Distribution