Physics 15 Torque (3 of 27) Tension=? in the Cable
TLDRThe video script presents a physics problem involving a beam of 250 kg mass held at a 40-degree angle to the horizontal by a string attached to the ceiling, with one end touching the frictionless floor. The problem aims to find the tension in the cable and the normal force exerted by the floor on the beam. Using the principle of torque equilibrium, the video calculates the distances from the pivot point to the lines of action of the forces involved. It then applies trigonometric functions to determine these distances in terms of the beam's length and the angles formed. The tension in the cable is found to be 2744 Newtons, and the normal force (the force the floor exerts on the beam) is calculated to be 703.6 Newtons. This demonstrates that the majority of the beam's weight is supported by the cable, with a relatively small force being exerted on the floor.
Takeaways
- 📐 The problem involves a beam held at an angle of 40 degrees with the horizontal by a string, with the other end touching the floor.
- ⚖️ The friction between the floor and the beam is assumed to be negligible, allowing for a smooth surface assumption.
- 🧷 The beam has a mass of 250 kilograms and the force of gravity acting on it (mg) is a key factor in the calculations.
- 🔄 The sum of the torques around the pivot point (end of the beam) must equal zero for the static situation.
- 📏 Distances from the forces to the pivot point (D1 and D2) are calculated using trigonometry based on the angles involved.
- 🤍 The tension in the cable (T) is found by setting up an equation where the sum of torques equals zero and solving for T.
- 📉 The force on the floor (F) is determined by ensuring the sum of forces in the Y-direction equals zero, considering the weight of the beam and the Y-component of the tension force.
- 🔢 The cosine of different angles (40 degrees and 70 degrees) is used to calculate the distances D1 and D2 from the forces to the pivot point.
- 🎢 The tension in the cable is calculated to be 2744 Newtons, which is a result of the weight of the beam and the angles involved.
- 🏡 The force exerted by the beam on the floor is found to be 703.6 Newtons, which is significantly less than the weight of the beam due to the tension in the cable.
- ⚙️ The problem-solving approach demonstrates the application of statics principles, including torque and force equilibrium, in a practical scenario.
Q & A
What is the mass of the beam in the problem?
-The mass of the beam is 250 kilograms.
What is the assumption made about the friction between the floor and the beam?
-It is assumed that the friction between the floor and the beam is equal to zero, which means it's negligible and can be ignored in the calculations.
At what angle is the beam held with respect to the horizontal?
-The beam is held at an angle of 40 degrees with the horizontal.
What is the significance of the angle between the cable and the beam?
-The angle between the cable and the beam is 160 degrees, which helps determine the other angles in the problem and is crucial for calculating the torques and forces involved.
What is the formula used to calculate the tension in the cable?
-The formula used is the sum of all the torques about the pivot point (end of the beam) being equal to zero: T * D1 = mg * D2, where T is the tension, D1 and D2 are the perpendicular distances from the lines of action of the forces to the pivot point, m is the mass, and g is the acceleration due to gravity.
How is the distance D1 related to the length of the beam and the angles involved?
-D1 is equal to the length of the beam times the cosine of 70 degrees, which is derived from the geometry of the right triangle formed by the beam, the cable, and the horizontal floor.
What is the calculated tension in the cable?
-The calculated tension in the cable is 2744 Newtons.
How is the force exerted by the beam on the floor determined?
-The force exerted by the beam on the floor is determined by ensuring that the sum of all forces in the Y-direction equals zero, which involves balancing the weight of the beam with the Y-component of the tension force.
What is the calculated force exerted by the beam on the floor?
-The calculated force exerted by the beam on the floor is 703.6 Newtons.
Why is the force exerted by the beam on the floor much less than the weight of the beam?
-Most of the weight of the beam is borne by the cable, resulting in a smaller force being exerted on the floor. This is due to the angles and the distribution of forces as per the problem's setup.
What is the significance of the torque equation in solving this problem?
-The torque equation is crucial as it allows us to calculate the unknown tension in the cable by setting up an equilibrium condition where the sum of torques around a chosen pivot point is zero.
How does the problem demonstrate the principle of static equilibrium?
-The problem demonstrates static equilibrium by showing that in a state of rest, the sum of all torques and forces in each direction must equal zero, which is used to solve for the unknown tension and force exerted on the floor.
Outlines
🔍 Static Equilibrium and Torque Analysis
This paragraph introduces a physics problem involving a beam of 250 kg mass, suspended at a 40-degree angle to the horizontal by a string attached to the ceiling, and resting on a frictionless floor. The problem aims to find the tension in the cable and the normal force exerted by the floor on the beam. The approach involves applying the principle of torques summing to zero, selecting an appropriate pivot point (the end of the beam), and considering the forces causing torque about this pivot, including the tension in the cable and the weight of the beam. The weight's center of mass is assumed to be at the beam's midpoint. The solution process involves setting up an equation based on torques and solving for the unknown tension, T.
📐 Calculating Distances and Tension in the String
The second paragraph delves into the specifics of calculating the distances (D1 and D2) from the forces' lines of action to the pivot point, which are necessary for determining the torques. It explains that D1 is found using the cosine of a 70-degree angle, derived from the geometry of the situation, and D2 is calculated using the cosine of a 40-degree angle, corresponding to the angle between the beam and the horizontal floor. The tension in the string (T) is then found by setting up an equation that the sum of the torques equals zero and solving for T, which yields a value of 2744 Newtons.
🧮 Finding the Normal Force on the Floor
The final paragraph addresses the calculation of the normal force (F) exerted by the floor on the beam. This is done by considering the forces in the Y-direction and setting up an equation where the sum of these forces equals zero. The normal force F is then found by rearranging the equation to solve for F, taking into account the weight of the beam (mg), and the Y-component of the tension force in the cable (T times the cosine of 30 degrees). The calculation results in a normal force of approximately 703.6 Newtons, illustrating that most of the beam's weight is supported by the cable, with a relatively small force exerted on the floor.
Mindmap
Keywords
💡Torque
💡Static Situation
💡Friction
💡Beam
💡Tension
💡Normal Force
💡Center of Mass
💡Sum of Forces
💡Angle of Incline
💡Cosine
💡Newton's Second Law
Highlights
The problem involves finding the tension in a cable and the normal force on a beam using torque and force balance concepts.
The beam has a mass of 250 kg and is held at a 40 degree angle with the horizontal by a cable attached to the ceiling.
Friction between the floor and beam is assumed to be negligible, allowing the reactionary force from the floor to be perpendicular to the beam.
The angle between the cable and the beam is 160 degrees, resulting in a 20 degree angle at the bottom.
The concept of summing torques equal to zero is applied, with the pivot point chosen at the end of the beam.
The tension in the cable and the weight of the beam (mg) are the two forces causing torques about the pivot point.
The center of mass of the beam is assumed to be at its halfway point, making it easier to calculate the torques.
The distances from the line of action of the forces to the pivot point (D1 and D2) are calculated using trigonometry.
The tension in the cable (T) is solved for by setting the sum of torques equal to zero and isolating T.
The force on the floor (normal force) is found by summing the forces in the Y direction and setting it equal to zero.
The Y component of the tension force is calculated using the cosine of the 30 degree angle between the tension force and the horizontal.
The final answers are T = 2744 N (tension in cable) and F = 703.6 N (normal force on floor).
The problem demonstrates how most of the beam's weight is supported by the cable, with only a small force being exerted on the floor.
The problem involves careful selection of pivot points and application of torque and force balance principles.
Trigonometry is used extensively to calculate distances and angles in the problem.
The problem requires a good understanding of statics and the ability to apply fundamental principles to solve complex problems.
The problem illustrates the importance of free body diagrams and the careful labeling of forces and distances.
The problem demonstrates the power of mathematical modeling and the ability to break down complex real-world problems into simpler components.
The problem requires attention to detail and the ability to keep track of different forces, distances, and angles.
Transcripts
Browse More Related Video
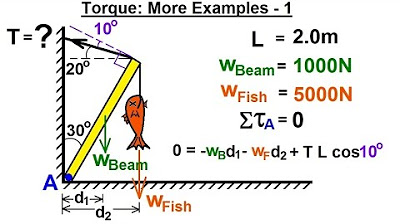
Physics 15 Torque (19 of 25) More Examples: 1 T=? of Cable Holding Fish
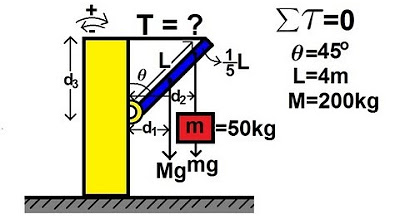
Physics 15 Torque Example 2 (2 of 7) Mass on Rod and Cable
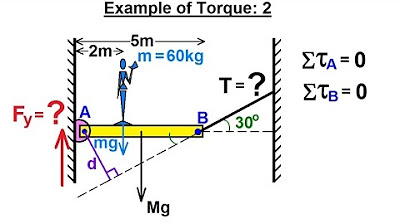
Physics 15 Torque (12 of 27) Example 2: Forces=? Tension=?
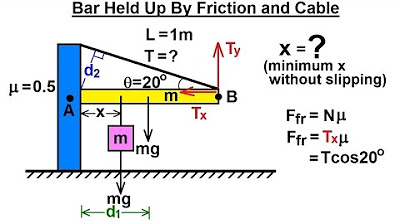
Physics 15 Torque (4 of 27) Bar Held Up by Friction
Physics 15 Torque (5 of 27) Tension=? Supporting a Gate

Torque Example #3: Leaning Ladder Problem
5.0 / 5 (0 votes)
Thanks for rating: