4.3 - Area and Definite Integrals
TLDRThis video script delves into the concept of calculating the area under the graph of a function, a fundamental topic in calculus. The discussion begins with the approximation of area using a Riemann sum, which involves breaking the area into rectangles and summing their areas. The script then transitions into the more precise method of calculating area through definite integrals, which involves finding antiderivatives of functions. The process of evaluating definite integrals is illustrated with several examples, emphasizing the cancellation of the constant of integration 'C' in these calculations. The video also addresses the interpretation of negative areas, which occur when a portion of the graph lies below the x-axis. Practical applications, such as calculating the total cost of installing a certain area of kitchen countertop using marginal cost functions, are also explored. The script concludes with a teaser for the next video, which will tackle the issue of negative area in more depth and introduce techniques for calculating the area between two graphs.
Takeaways
- 📐 **Riemann Sum**: The area under a curve can be approximated by breaking it into rectangles and summing their areas, known as a Riemann sum.
- 🔍 **Rectangle Width (Δx)**: The width of each rectangle in the approximation is constant and is represented by Δx.
- 📈 **Function Values**: The height of each rectangle is determined by the function's value at a particular x-coordinate.
- 🔢 **Increasing Accuracy**: More rectangles (smaller Δx) lead to a more accurate approximation of the area under the curve.
- ∞ **Limit of Infinite Rectangles**: As the number of rectangles approaches infinity, the approximation approaches the actual area under the curve.
- 🛠️ **Numerical Calculations**: For a large number of rectangles, numerical methods are used to approximate the area, which is impractical to do by hand.
- 🆕 **Definite Integral**: The exact area under a curve is found using a definite integral, which involves antiderivatives.
- 📉 **Negative Area**: Areas below the x-axis are considered negative, and the definite integral accounts for this by giving a net area that may be negative if more area lies below the x-axis.
- ∫ **Integration**: The process of finding antiderivatives and evaluating them at the limits of integration is known as integration.
- 💰 **Applied Problem**: Definite integrals can be used to solve real-world problems, such as calculating the total cost of installing a certain area of kitchen countertop.
- 🔄 **Total vs. Net Area**: The definite integral gives the net area between the curve and the x-axis, which may require additional manipulations to find the total area when the curve dips below the x-axis.
Q & A
What is a Riemann sum and how is it used to estimate the area under a curve?
-A Riemann sum is a method used to approximate the area under a curve by breaking it down into a series of rectangles. The area under the graph of a function is approximated by summing the product of the function value at a point and the width of the rectangles (delta x) across a sequence of x values from 1 to n.
How does the number of rectangles used in a Riemann sum affect the accuracy of the area approximation?
-The fewer rectangles used, the less accurate the area approximation. Conversely, using more rectangles increases the accuracy of the area calculation. As the number of sub-intervals approaches infinity, the approximation becomes more precise and tends towards the actual area under the curve.
What is the purpose of the term 'delta x' in the context of a Riemann sum?
-'Delta x' represents the common width of each of the n sub-intervals into which the area under the curve is divided. It is used to determine the height of each rectangle in the rectangular approximation method.
How does the concept of limits relate to the process of increasing the number of rectangles to approximate the area under a curve?
-The concept of limits is used to numerically approach the actual area by increasing the number of sub-intervals (rectangles). As the number of rectangles increases, the approximation gets closer to the actual area, and in the limit as the number of sub-intervals approaches infinity, the approximation equals the actual area.
What is a definite integral and how does it differ from a Riemann sum?
-A definite integral is a mathematical concept that allows for the exact calculation of the area under a curve without approximation. It uses the antiderivative of the function and evaluates it at the upper and lower limits of integration, then subtracts the two. Unlike a Riemann sum, which is an approximation, a definite integral provides an exact value for the area.
Why does the constant of integration (C) not matter when calculating a definite integral?
-The constant of integration (C) is not relevant when calculating a definite integral because it cancels out when evaluating the antiderivative at the upper and lower limits and subtracting the two. The definite integral is concerned with the difference in values, which is independent of any constant.
What is the role of antiderivatives in the process of integration?
-Antiderivatives are used to find the exact area under a curve by performing integration. They represent the reverse process of differentiation, and when evaluated at specific limits, they yield the value of the definite integral, which is the area under the graph of the function.
How are definite integrals used in practical applications, such as calculating total costs?
-Definite integrals can be used to calculate the total cost of a project by integrating the marginal cost function over a specific interval. This provides the total cost of producing a certain quantity of goods, such as installing a certain number of square feet of kitchen countertop.
What does it mean when the result of a definite integral is negative?
-A negative result from a definite integral indicates that there is more area under the curve below the x-axis than above it. This does not mean that the calculation is wrong, but rather that the function has portions that dip below the x-axis, contributing negatively to the total area.
How can the concept of definite integrals be used to find the total area between two curves?
-Definite integrals can be manipulated to find the total area between two curves by calculating the integral of the difference between the two functions over the given interval. This approach allows for the calculation of areas even when one of the curves lies below the x-axis.
What is the significance of the limits of integration in a definite integral?
-The limits of integration in a definite integral specify the interval over which the function is integrated. The lower limit is always the smaller value, and the upper limit is the larger value, indicating the start and end points of the area calculation under the curve.
Outlines
📊 Understanding Riemann Sums for Area Calculation
This paragraph introduces the concept of calculating the area under a curve using Riemann sums. It explains that the area between the curve and the x-axis can be approximated by summing the function values across a sequence of x-values, each multiplied by a common width delta x. The more rectangles used in the approximation, the closer the sum gets to the actual area. The limit of this process as the number of rectangles approaches infinity gives the exact area under the curve.
🧮 The Definite Integral as Exact Area Calculation
The paragraph discusses the definite integral as a method to calculate the exact area under a curve without approximation. It explains that the definite integral from a to b is found by taking the antiderivative of the function and evaluating it at points a and b, then subtracting the two. This process, known as integration, yields a constant value representing the exact area. The constant of integration, denoted by 'c', is not relevant when calculating definite integrals and thus can be omitted.
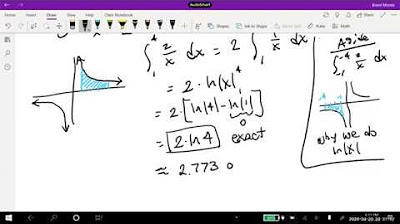
🔢 Evaluating Definite Integrals with Examples
This paragraph provides step-by-step examples of calculating definite integrals. It covers the process of finding antiderivatives, evaluating them at the limits of integration, and subtracting the results. The examples illustrate how to handle different types of functions, including polynomial and exponential functions, and how to deal with the constant of integration, which cancels out in definite integrals.
📈 Interpreting Definite Integrals Graphically
The paragraph explains how to interpret definite integrals graphically. It clarifies that the value obtained from a definite integral represents the area under the graph of the function over a given interval. The paragraph also discusses the graph of a function and its area over an interval, emphasizing how the definite integral provides the exact area.
🤔 Dealing with Negative Areas in Definite Integrals
This paragraph addresses the issue of negative areas in definite integrals. It explains that areas below the x-axis are considered negative, and when a function's graph lies both above and below the x-axis, the enclosed areas can negate each other. The paragraph also mentions that if the total area is negative, it means there is more area below the x-axis than above it.
🛠️ Application of Definite Integrals in Cost Analysis
The paragraph demonstrates the application of definite integrals in calculating total costs, using the example of a general contractor's marginal cost for installing kitchen countertops. It shows how to find the total cost of installing a certain number of square feet by integrating the marginal cost function over the desired interval.
📐 Evaluating Total and Additional Costs Using Definite Integrals
This paragraph continues the application of definite integrals in cost analysis by calculating the total cost of installing a certain area of countertops and the additional cost of installing extra square footage. It shows how to adjust the limits of integration to account for the additional area and how to interpret the results in terms of cost.
🔄 Further Exploration of Area Calculations
The final paragraph summarizes the concept of area calculations using definite integrals and Riemann sums. It mentions the issue with negative areas and hints at future discussions on how to calculate the total area without worrying about negative values. The paragraph also teases the topic of area between two graphs as a way to address the negative area issue.
Mindmap
Keywords
💡Riemann Sum
💡Anti-derivative
💡Definite Integral
💡Limits of Integration
💡Constant of Integration
💡Negative Area
💡Marginal Cost
💡Total Cost
💡Integration
💡Power Rule
💡Natural Logarithm
Highlights
The area under the graph of a function can be estimated using a Riemann sum, which is an approximation method breaking the area into rectangles.
Riemann sum is calculated by summing the function values across a sequence of x-values, each multiplied by delta x.
The accuracy of the area approximation increases with the number of rectangles used in the Riemann sum.
The concept of limits is used to approach the area calculation as the number of sub-intervals approaches infinity.
Definite integrals provide an exact method to calculate the area under a curve without approximation.
The definite integral is calculated by finding the antiderivative of the function and evaluating it at the limits of integration.
The constant of integration (C) is not relevant when calculating definite integrals as it cancels out in the evaluation process.
The value of a definite integral represents the actual area under the graph of the function over a given interval.
The limits of integration in a definite integral are always in increasing order, with the lower limit being smaller than the upper limit.
The process of evaluating a definite integral involves finding the antiderivative, substituting the limits of integration, and subtracting the results.
The area under a curve can be positive or negative, with negative indicating the region below the x-axis.
Total area calculation can be affected by negative areas, which represent regions below the x-axis.
The concept of accumulation is central to integrals, which represent the total change or sum as opposed to the instantaneous rate of change represented by derivatives.
An applied problem demonstrates how to use definite integrals to calculate total costs in a real-world scenario, such as installing kitchen countertops.
The total cost of installing a certain area can be found by integrating the marginal cost function over the desired interval.
The cost of installing additional square footage can be determined by evaluating the definite integral from the initial area to the new total area.
The video concludes with a discussion on handling negative areas and the concept of area between two curves, which will be explored in more depth in the next video.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: