Math 11 - Section 4.3
TLDRIn this educational video, Professor Monte dives into Section 4.3, focusing on the concept of area and definite integrals. He begins by illustrating how the area under a curve between two points can be calculated using definite integrals, which is essentially the total change in the function over that interval. The discussion then transitions to the Fundamental Theorem of Calculus, which provides a method for calculating these areas without the need for approximation. The theorem is presented in a simplified manner to avoid confusion, emphasizing the relationship between the derivative and the antiderivative. Throughout the video, Professor Monte works through several examples, including calculating the area under a constant function, a cubic function, and a reciprocal function. He also touches on the practical applications of definite integrals, such as determining total cost in business contexts. The video concludes with an application problem involving the cost of installing kitchen countertops, demonstrating how to calculate the cost of additional installation beyond an initial amount. The summary effectively conveys the instructional nature of the content and the practical use of definite integrals.
Takeaways
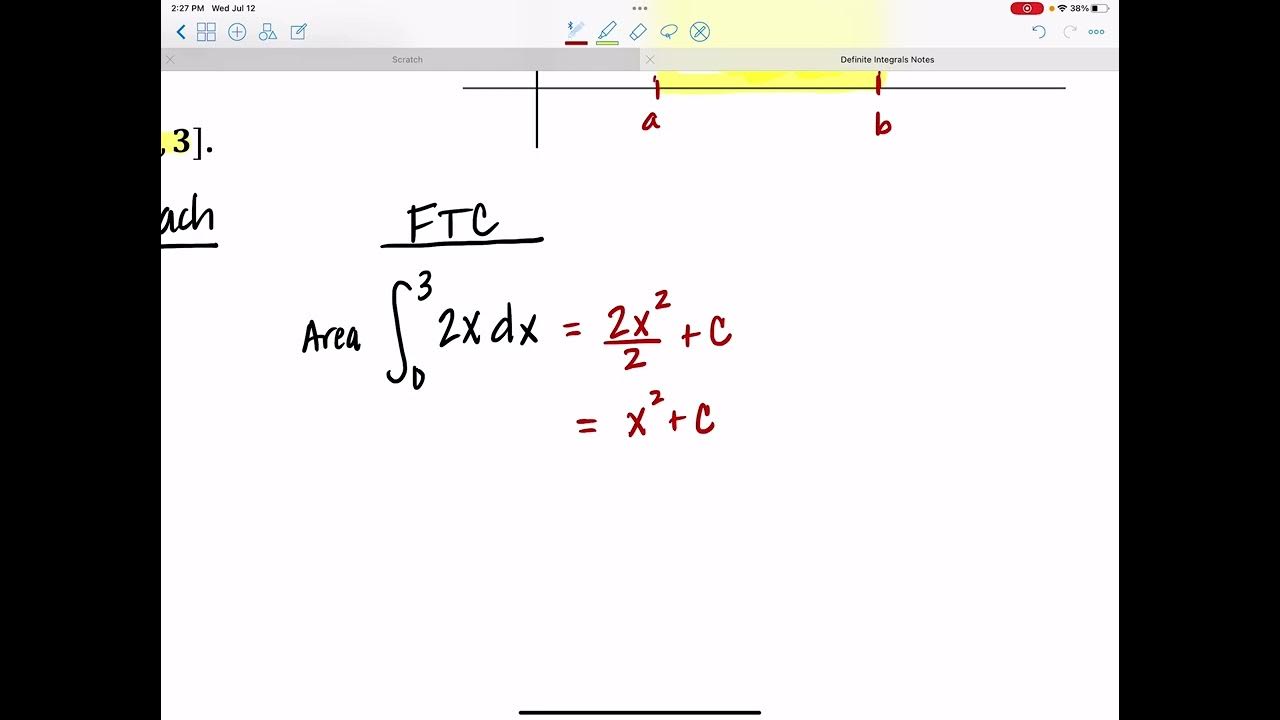
- 📚 The definite integral from A to B of a function f(x) represents the total change in the function or the area under the curve between those points.
- 🧮 The Fundamental Theorem of Calculus allows us to find the definite integral by finding the antiderivative of the function and evaluating it at the limits A and B.
- 📈 When dealing with a linear function, the area under the curve can be found using basic geometry or by using the Fundamental Theorem of Calculus.
- 🔢 For more complex functions, the definite integral can be found without approximation by using the antiderivative and the Fundamental Theorem of Calculus.
- ∫ When evaluating a definite integral, the constant of integration (+C) is not included because we are interested in the exact area between the curve and the x-axis.
- 🏗 In practical applications, such as calculating total cost or total kilowatt usage, the definite integral of the marginal cost or rate of change function gives the total amount.
- 🤔 The sign of the definite integral (positive, negative, or zero) can be determined visually by examining the curve and identifying areas above and below the x-axis.
- 📉 The area under a curve that lies below the x-axis contributes negatively to the total integral, reflecting concepts like negative profit in business.
- 📌 The process of evaluating a definite integral involves finding an antiderivative, applying the limits of integration, and calculating the difference.
- 📐 The concept of the definite integral is central to understanding calculus and its applications in various fields such as physics, engineering, and economics.
- 💡 Memorizing the formula for the Fundamental Theorem of Calculus and practicing its application is key to solving problems involving definite integrals.
Q & A
What is the main topic of discussion in the transcript?
-The main topic of discussion is section 4.3 area and definite integrals, focusing on the concept of definite integrals, the fundamental theorem of calculus, and its applications to find areas under curves and total changes in functions.
How is the area under a function between two points A and B represented?
-The area under a function between two points A and B is represented by the definite integral from A to B of the function f(X) with respect to X, denoted as ∫ from A to B f(X) dX.
What does the fundamental theorem of calculus state?
-The fundamental theorem of calculus states that if a continuous function f has an antiderivative F over the closed interval A to B, then the definite integral from A to B of f(X) dX is equal to F(B) - F(A), which represents the total change in the function or the area under the curve between those two points.
How does the professor suggest simplifying the expression of the fundamental theorem of calculus?
-The professor suggests writing the fundamental theorem as the integral from A to B of the derivative of the function (f'(X)), then taking the antiderivative to get back to the original function, and evaluating it at B and A, which simplifies the expression and avoids confusion with the antiderivative notation (capital F).
What is the purpose of using the absolute value when calculating the definite integral of a function like 2/X?
-The absolute value is used to ensure that the result of the natural logarithm function is defined, as the natural logarithm of a negative number is not defined in the real number system. It also correctly represents the area under the curve, even when integrating over a range that includes negative values.
How does the area under a marginal cost function relate to total cost?
-The area under a marginal cost function represents the total cost. This is because the marginal cost function represents the cost per unit, and integrating it over a range of units gives the total cost for that range, as each unit's marginal cost contributes to the overall total cost.
What is the significance of the sign (positive or negative) of a definite integral?
-The sign of a definite integral indicates whether the area under the curve is above or below the x-axis. A positive integral indicates that there is more area above the x-axis, while a negative integral indicates that there is more area below the x-axis.
How does the professor demonstrate the process of evaluating a definite integral in the context of a word problem?
-The professor demonstrates by providing a word problem about the cost of installing kitchen countertops. The marginal cost function is given, and the definite integral from 0 to the number of square feet is calculated to find the total cost. The process involves finding the antiderivative of the marginal cost function and evaluating it at the given limits.
What is the role of the constant in a definite integral, and how is it treated during the evaluation process?
-The constant in a definite integral acts as a multiplier for the integrated function. During the evaluation process, the constant remains with the function as the exponent of the variable is increased by one and the reciprocal of the new exponent is taken. When evaluating the definite integral, the constant is multiplied by the difference of the function values at the upper and lower limits of integration.
Why is it important to consider the limits of integration when calculating a definite integral?
-The limits of integration are crucial as they define the interval over which the function is integrated. The definite integral represents the exact area under the curve between these limits or the total change in the function over this interval. Without the correct limits, the integral would not accurately reflect the desired quantity.
How does the concept of definite integrals apply to real-world scenarios such as calculating total costs or quantities?
-Definite integrals can be applied to real-world scenarios by representing the accumulation of small changes over a given interval. For instance, in business, the marginal cost function can be integrated to find the total cost of producing a certain number of items. Similarly, in physics, the concept can be used to calculate the total distance traveled by an object given its velocity function over time.
Outlines
📚 Introduction to Area and Definite Integrals
Professor Monte begins by introducing the topic of area and definite integrals from section 4.3. He explains the concept of the area under a curve (function f(x)) between two points A and B, which is equivalent to the total change in the function over that interval. The definite integral is represented as an integral from A to B of f(x) with respect to x. The Fundamental Theorem of Calculus is introduced, which relates antiderivatives to definite integrals, and an example is provided to illustrate the process of finding the area under the curve as the difference between the function values at points B and A.
📝 Simplifying the Fundamental Theorem for Definite Integrals
The professor simplifies the expression of the Fundamental Theorem of Calculus to make it more intuitive. He demonstrates how to find the definite integral of a derivative function from A to B by evaluating the original function at point B and then at point A, thus avoiding confusion with the antiderivative notation. An example using marginal cost is given to show how the theorem can be applied to find total cost over a specified interval.
🔍 Evaluating Definite Integrals with Linear and Cubic Functions
The professor provides examples of calculating definite integrals for a constant function (y=5) and a cubic function (y=x^3) over specific intervals. He shows that the definite integral can be found using the fundamental theorem without the need for approximation, and that it represents the exact area under the curve. The process involves integrating the function and evaluating it at the upper and lower limits of the interval.
🧮 Definite Integrals of a Rational Function and the Concept of Asymptotes
The focus shifts to definite integrals of the rational function y = 2/x from 1 to 4. The professor discusses the graph of the function, which has a horizontal asymptote along the x-axis and a vertical asymptote along the y-axis. The integral is evaluated by recognizing the antiderivative of 1/x as ln|x|, and the absolute value is used to ensure the argument of the natural logarithm is positive. The final answer is given both as an exact value and an approximate decimal.
📈 Interpreting the Area Under the Curve as Total Change
The professor explains the significance of the area under the curve of a derivative function, such as marginal cost or rate of change of kilowatts used per hour. He clarifies that this area represents the total change in the original function, which could be total cost or total kilowatts used, depending on the context. The concept is illustrated with an example involving cost and the summation of marginal costs to find total cost.
🖼️ Visual Determination of Definite Integrals' Sign
The script involves a visual assessment of definite integrals to determine whether they are positive, negative, or zero. The professor discusses how the sign of the integral can be inferred from the graph of the function, with areas below the x-axis contributing negatively to the integral and areas above contributing positively. Two parts are covered, each with a different function and interval, leading to the conclusion of the integral's sign without explicit calculation.
🔢 Evaluating Definite Integrals and Comparing Areas Above and Below the Axis
The professor addresses a problem that asks to evaluate a definite integral from 0 to 2 of x^2 and determine if there's more area above or below the x-axis. By calculating the integral and comparing the result to zero, it's concluded that there is more area above the curve, resulting in a positive value. The process involves integrating the function and evaluating it at the specified limits.
🏗️ Application of Definite Integrals in Business Costing
The professor concludes with a practical application of definite integrals, calculating the total cost of installing a certain area of kitchen countertop. The marginal cost function is given, and the definite integral from 0 to the area of the countertop is evaluated to find the total cost. An additional query about the cost of installing extra countertop space is also addressed by evaluating the integral over the extended area.
📝 Summary of Definite Integrals Calculation and Its Significance
The professor summarizes the process of calculating definite integrals, emphasizing their representation of the total change in a function or the area under the curve between two points. He encourages students to practice these calculations and to participate in live sessions for further discussion and clarification of doubts.
Mindmap
Keywords
💡Definite Integrals
💡Antiderivative
💡Fundamental Theorem of Calculus
💡Marginal Cost
💡Total Cost
💡Area Under the Curve
💡Integration Limits
💡Plus C
💡Total Kilowatt-Hours
💡Visual Evaluation of Integrals
💡Constant Multiple Rule
Highlights
Introduction to section 4.3 on area and definite integrals.
Explanation of the area under a function between two points a and B as the total change in the function.
The fundamental theorem of calculus is introduced as a key concept for understanding definite integrals.
Demonstration of how to write the area under a curve as an integral from A to B of f(X) with respect to X.
Use of the fundamental theorem to find the total area under the curve without approximation.
Illustration of how to calculate the definite integral of a function by finding the antiderivative and evaluating it at the limits of integration.
Example problem showing how to find the area under the curve y=5 between x=1 and x=3.
Explanation of why the constant C is not included in definite integrals but is in indefinite integrals.
Application of the fundamental theorem to find the total kilowatt usage over a period of time given the rate of change.
Use of definite integrals to determine the total cost from a marginal cost function.
Visual determination of whether a definite integral is positive, negative, or zero based on the curve's position relative to the x-axis.
Solution of a word problem involving the cost of installing a certain area of kitchen countertop using marginal cost.
Calculation of the cost of installing an additional area of countertop after an initial installation.
Emphasis on the importance of understanding definite integrals for the rest of the semester.
The total change in a function or the area under the curve between two points is represented by the definite integral.
Practical application of definite integrals in business calculations, such as total costs.
Encouragement for students to practice and understand the concept of definite integrals for application in various problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: