What Is an Integral?
TLDRThe video script explains the concept of estimating the area under a curve using rectangles, which is the basis for the Riemann sum and integral. It discusses how increasing the number of rectangles leads to a better approximation of the area. The script then transitions into the mathematical representation of this concept, introducing the Riemann sum and its limit as the number of rectangles approaches infinity, resulting in the Riemann integral. The integral is interpreted as the net area between the curve and the x-axis, with positive and negative areas representing areas above and below the x-axis, respectively. The script concludes by introducing the fundamental theorem of calculus, which links differentiation and integration, and explains how it can be used to evaluate indefinite integrals.
Takeaways
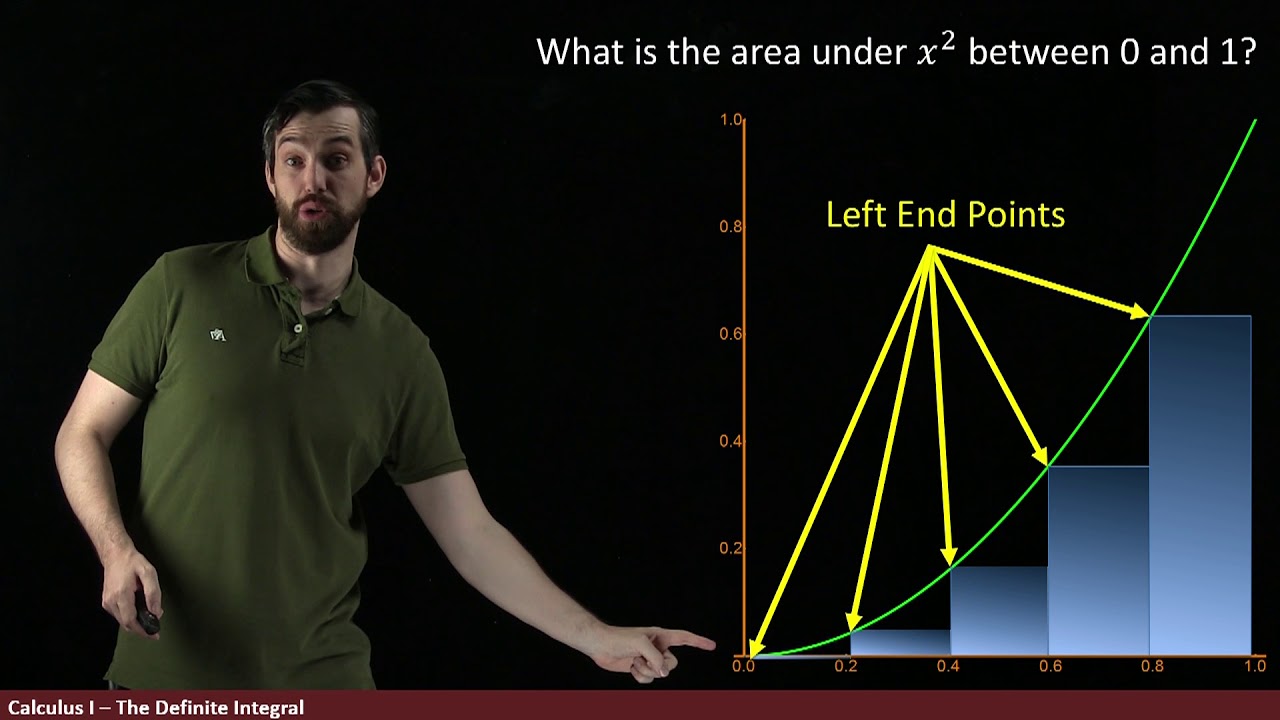
- 📊 Estimating the area under a curve can be done by dividing the region into segments and using rectangles to approximate the area.
- 🔍 The more rectangles used (narrower they are), the better the estimate of the area under the curve becomes.
- 📐 The process of estimating the area under a curve with rectangles is translated into a mathematical concept using Riemann sums.
- 🌟 Riemann sums involve calculating the area of rectangles under the curve for equally sized regions defined by x-coordinates (x0, x1, x2, ..., xn).
- 📈 The sum of rectangle areas, denoted as S_n, represents an approximation of the area under the curve and is improved as n (number of rectangles) increases.
- 🏓 The limit of S_n as n approaches infinity provides the exact area under the curve, which is the Riemann integral, represented symbolically as an integral from x0 to xn.
- 🔄 The Riemann integral can be interpreted as a net area between the function and the x-axis, with positive areas above the x-axis and negative areas below it.
- 📚 Definite integrals are written as the integral from A to B of a function times a differential width, where A and B are constants.
- 🎓 The fundamental theorem of calculus links differentiation and integration, stating that the derivative of an indefinite integral is the original function.
- 🔄 Indefinite integrals result in a function (capital F of X) when the upper limit is a variable, and they are useful for finding the antiderivative of a function.
- 🔧 The process of finding an indefinite integral often involves adding a constant of integration (C) to account for the arbitrary nature of the integration variable.
Q & A
What is the basic concept of estimating the area under a curve using rectangles?
-The basic concept involves dividing the area under the curve into smaller segments and approximating each segment with a rectangle. The sum of the areas of these rectangles provides an estimate of the area under the curve.
How does increasing the number of rectangles improve the estimate of the area under the curve?
-Increasing the number of rectangles makes each rectangle narrower, which allows them to fit better under the curve. This results in a more accurate estimate of the area under the curve as the rectangles more closely approximate the shape of the curve.
What are the different ways to position the rectangles to estimate the area under the curve?
-The rectangles can be positioned with their upper right corner, upper left corner, or top center touching the curve. The choice of positioning does not affect the ability of the rectangles to provide an estimate of the area under the curve, as long as they are narrow enough to fit well under the curve.
What is a Riemann sum and how is it related to estimating the area under a curve?
-A Riemann sum is a mathematical concept used to estimate the definite integral of a function over an interval by summing the areas of rectangles inscribed within the curve. It is named after the mathematician Bernhard Riemann and is used to approximate the area under a curve as the number of rectangles increases.
How does the fundamental theorem of calculus relate to Riemann sums and integration?
-The fundamental theorem of calculus establishes a relationship between differentiation and integration. It states that the derivative of the indefinite integral of a function is equal to the original function. This theorem provides a practical way to evaluate indefinite integrals by finding the function that, when differentiated, yields the function being integrated.
What is the significance of the net area in the Riemann integral definition?
-The Riemann integral is defined as the net area between the function and the x-axis over an interval. This means that areas below the x-axis are considered negative and areas above the x-axis are positive. The Riemann integral then represents the sum of these areas, which can be interpreted as a net geometric area only when the function is always positive over the interval.
How can the area under a curve be negative in the context of the Riemann integral?
-A negative area under a curve in the context of the Riemann integral occurs when the function is negative over the interval considered. Since areas below the x-axis are considered negative, a function that is always negative will result in a negative Riemann integral, indicating a net area below the x-axis.
What is the difference between a definite integral and an indefinite integral?
-A definite integral has a specific upper and lower limit and represents the signed area between the curve and the x-axis over a particular interval. An indefinite integral, on the other hand, does not have fixed limits and represents a family of functions, one for each constant of integration, that could be the original function when differentiated.
How do you calculate the area of a rectangle used in estimating the area under a curve?
-The area of a rectangle is calculated by multiplying its height, which is the value of the function at a specific x-coordinate, by its width, which is the difference between the x-coordinates of the right and left sides of the rectangle (Δx).
What is the geometric interpretation of a Riemann integral?
-The geometric interpretation of a Riemann integral is the area between the curve and the x-axis over a given interval. This interpretation is valid when the function lies above the x-axis, and the area is taken as a positive value. If the function lies below the x-axis, the area is considered negative, and the Riemann integral represents the net area.
What is the role of the constant of integration in indefinite integrals?
-The constant of integration, often denoted as C, is added to the indefinite integral to account for the arbitrary constant that appears when anti-differentiating a function. It reflects the fact that an indefinite integral represents a family of functions that differ by a constant.
Outlines
📊 Estimating Area Under a Curve with Rectangles
This paragraph discusses the method of estimating the area under a curve using rectangles. It begins with a simple approach of dividing the region into four segments and drawing rectangles that poorly fit under the curve. The estimate is improved by increasing the number of rectangles, which better fit the curve. The concept is then translated into mathematical terms, introducing the idea of Riemann sums and the Riemann integral. The explanation includes the geometric interpretation of the Riemann integral and the symbolic representation of the integral as the area between the curve and the x-axis over a given interval.
📈 Riemann Integral and its Geometric Interpretation
This paragraph delves into the Riemann integral, explaining its geometric interpretation as the area between the curve and the x-axis. It highlights that the Riemann integral can be positive or negative depending on whether the function lies above or below the x-axis. The paragraph also introduces the concept of a net area, where areas below the x-axis are considered negative. The fundamental theorem of calculus is mentioned, which connects differentiation and integration, and provides a method for evaluating indefinite integrals by finding a function whose derivative equals the function being integrated.
Mindmap
Keywords
💡Area under a curve
💡Riemann sum
💡Integration
💡Definite integral
💡Indefinite integral
💡Fundamental theorem of calculus
💡Rectangle method
💡Net area
💡Constant of integration
💡Differential width
Highlights
Estimating the area under a curve by dividing the region into segments and using rectangles.
Improving the estimate by increasing the number of rectangles used.
The concept of fitting rectangles to estimate the area under a curve can be translated into mathematics.
Using three equally sized regions to estimate the area under the curve with rectangles.
The sum of the areas of the rectangles, denoted as S_sub_3, provides an approximation of the area under the curve.
The Riemann sum, S_sub_n, is the sum of the areas of n rectangles and serves as an estimate of the area under the curve.
The limit of S_sub_n as the number of rectangles goes to infinity provides a precise estimate of the area under the curve.
The integral, represented as the area between the curve and the x-axis, is a fundamental concept in calculus.
A Riemann integral can be interpreted geometrically as the area between the curve and the x-axis, but only if the function is always positive.
The Riemann integral is refined to account for the net area, including negative areas below the x-axis.
Definite integrals are written as the integral from A to B of a function times a differential width, where A and B are constants.
Indefinite integrals involve replacing the upper limit B with a variable X, resulting in a function of X.
The fundamental theorem of calculus states that the derivative of an indefinite integral is equal to the function being integrated.
Differentiation and integration are inverse processes, allowing for the calculation of indefinite integrals.
The integral of cosine X is sine X, plus a constant of integration.
The process of estimating areas under curves and the development of integral calculus have significant practical applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: