Bohr's Atomic Model
TLDRThe video script offers an in-depth exploration of Niels Bohr's atomic model, a significant advancement in understanding atomic structure that addressed the limitations of previous models. It begins with a historical overview, highlighting how scientists like Dalton, Thomson, and Rutherford contributed to the evolving understanding of the atom. The script then delves into Bohr's model, explaining its key postulates: electrons orbit the nucleus in fixed paths with quantized energy levels, and energy is absorbed or released during electron transitions, which corresponds to discrete spectral lines. The video also covers the quantization condition, where the angular momentum of an electron is an integer multiple of Planck's constant. The script further explains how Bohr's model rectifies the stability issue of atoms and explains the atomic spectrum. It concludes with a discussion of the model's limitations and a teaser for the upcoming quantum model by Schrödinger, inviting viewers to continue their exploration of atomic theory.
Takeaways
- 📚 The atomic model has evolved over time, starting with Dalton's solid sphere model in 1807, to Thompson's plum pudding model in 1897, Rutherford's nuclear model in 1911, and finally Niels Bohr's planetary model in 1913.
- 🌟 Niels Bohr challenged Albert Einstein and is famous for his atomic model where electrons revolve in fixed orbits or shells around the nucleus, with each shell having a fixed energy level.
- ⚛️ Bohr's model introduced the concept of quantization, stating that electrons can only occupy certain allowed orbits with specific energy levels, determined by the condition that the angular momentum is an integer multiple of ℏ (reduced Planck's constant).
- ⏳ The stability of atoms was a problem for Rutherford's model, as it couldn't explain why electrons don't radiate energy and collapse into the nucleus, a flaw that Bohr's model rectified by defining quantized orbits.
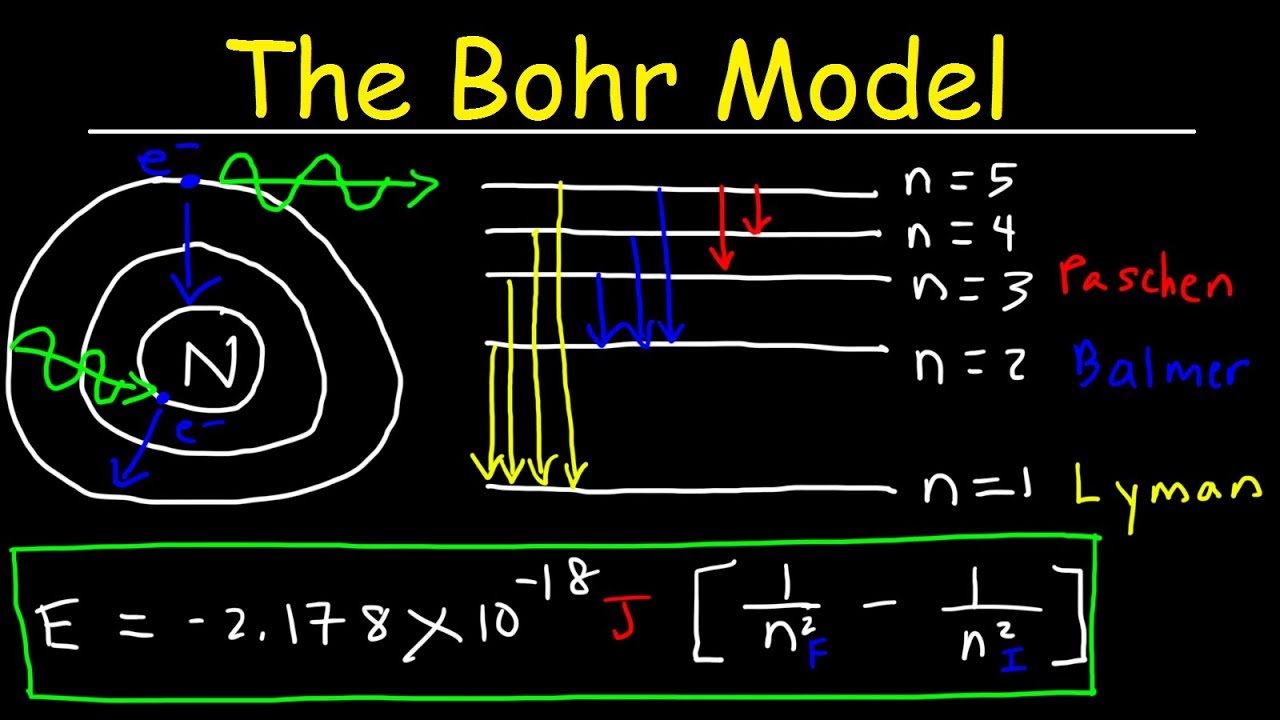
- 🌈 The line or atomic spectrum, which shows discrete lines of color for elements like hydrogen, could not be explained by Rutherford's model but was accounted for in Bohr's model through quantized energy levels.
- ⚡️ Electrons can gain or lose energy by moving to higher or lower energy shells, a process known as excitation and de-excitation, respectively, which involves the absorption or emission of specific amounts of energy.
- 🔢 The energy levels in an atom can be calculated using the formula E = -13.6 * Z^2 / n^2 electron volts, where Z is the atomic number and n is the shell number, indicating that energy increases as electrons move to higher shells.
- 🚀 The velocity of an electron in a particular shell can be determined by the formula v = 2.18 * 10^6 * Z / n, demonstrating that the electron's speed is influenced by the atomic number and the shell it occupies.
- ⛔ The potential energy of an electron in a shell is negative, reflecting the attraction between the negatively charged electron and the positively charged nucleus, with the formula PE = -2 * 13.6 * Z / n electron volts.
- 🔄 The total energy of an electron in a shell is the sum of its kinetic and potential energy and is given by TE = -3.6 * Z^2 / n^2 electron volts, which is negative because electrons in atoms have less energy than if they were free (at infinity).
- 🔬 Bohr's model, while successful in explaining the hydrogen atom and single-electron ions, has limitations and does not accurately describe more complex atoms with multiple electron shells, leading to the development of the quantum mechanical model by Schrödinger.
Q & A
Who proposed the planetary model of the atom?
-Niels Bohr proposed the planetary model of the atom, which was an improvement over Rutherford's model.
What was the main issue with Rutherford's model of the atom?
-The main issue with Rutherford's model was that it could not explain the stability of atoms. According to Maxwell's electromagnetic theory, electrons should lose energy and collapse into the nucleus, which contradicted the known stability of atoms.
What is the quantization condition in Bohr's atomic model?
-The quantization condition in Bohr's atomic model states that electrons can only revolve in certain fixed orbits where the angular momentum of the electron is an integer multiple of ħ (h-bar, which is Planck's constant divided by 2π).
How does Bohr's model explain the atomic spectrum?
-Bohr's model explains the atomic spectrum by stating that when electrons gain or lose energy, they move to different shells, and this transition results in the emission or absorption of radiation at specific frequencies. This quantized emission and absorption of energy corresponds to the observed line spectra of elements.
What is the significance of Planck's constant in Bohr's model?
-Planck's constant (h) is crucial in Bohr's model as it determines the quantization of energy levels and orbits of electrons. It is used in the formula to calculate the allowed orbits and energy levels of electrons within an atom.
How does the velocity of an electron in an atom's shell relate to its energy level?
-The velocity of an electron in an atom's shell is related to its energy level through the centripetal force provided by the electrostatic force between the positively charged nucleus and the negatively charged electron. The higher the energy level (further from the nucleus), the greater the velocity of the electron.
What is the formula for calculating the radius of an electron shell in a hydrogen atom?
-The formula for calculating the radius (R) of an electron shell (n-th shell) in a hydrogen atom is R = 0.53 * n² / Z, where n is the shell number and Z is the atomic number.
What is the relationship between the kinetic energy and potential energy of an electron in an atom?
-The potential energy of an electron in an atom is negative and is related to its distance from the nucleus. The kinetic energy is positive and depends on the electron's motion. The total energy of the electron is the sum of its kinetic and potential energies, and it is also negative, indicating that energy is required to remove the electron from the atom.
How does the total energy of an electron change as it moves to higher shells?
-As an electron moves to higher shells (increases n, the shell number), the total energy of the electron increases. This is because the negative value of the total energy becomes less negative, indicating a higher energy state.
What is the concept of excitation and de-excitation in the context of electrons in an atom?
-Excitation occurs when an electron gains enough energy to move to a higher energy level or shell. De-excitation is the opposite process where an electron loses energy and moves to a lower energy level or shell. Both processes involve the quantized absorption or emission of energy, which corresponds to specific frequencies of electromagnetic radiation.
Why is the atomic spectrum of elements such as hydrogen composed of discrete lines rather than a continuous range of colors?
-The atomic spectrum is composed of discrete lines because electrons can only exist in certain quantized energy levels. When electrons transition between these levels, they emit or absorb radiation at specific frequencies, which correspond to the observed lines in the spectrum.
Outlines
🌟 Introduction to Bohr's Atomic Model
The video begins with an introduction to Niels Bohr, the scientist who challenged Einstein and won the Nobel Prize for his work on the structure of the atom. The focus is on Bohr's atomic model, which improved upon Rutherford's model by explaining the stability of atoms and their electron configurations. The video promises to clarify the postulates of Bohr's model and discusses the historical context of atomic models, starting with Dalton's solid sphere model, through Thompson's plum pudding model, and leading up to Rutherford's nuclear model.
🔬 Drawbacks of Rutherford's Model and Bohr's Quantum Leap
The second paragraph delves into the limitations of Rutherford's model, particularly its inability to explain the stability of atoms and the discrete line spectrum of elements like hydrogen. It then introduces Bohr's model, which posited that electrons occupy fixed orbits with quantized energy levels. This model successfully explained the line spectrum and proposed that electrons can only gain or lose specific amounts of energy when transitioning between these orbits.
📚 Bohr's Postulates and the Atomic Structure
This paragraph outlines the key postulates of Bohr's atomic model. It explains that electrons revolve around the nucleus in fixed circular orbits with specific radii and energies. The quantization condition is introduced, stating that only certain orbits with specific angular momenta are allowed, which are integer multiples of Planck's constant divided by 2π. The video also discusses the third postulate, which allows for electrons to gain or lose energy by moving to higher or lower shells, and the associated radiation frequency emitted or absorbed during these transitions.
🚀 Visualizing the Atomic Model and Electron Orbits
The video provides a visualization of Bohr's atomic model, likening it to the solar system with planets revolving around the sun. It emphasizes that electrons are constrained to specific orbits or shells with fixed radii and energies. The concept of 'shells' is introduced, with labels K, L, M, etc., for successive electron shells. The video also touches on the electrostatic force that keeps the electrons in orbit, comparing it to the gravitational force in the solar system.
🔧 Derivation of Electron Orbital Radius
The paragraph details the mathematical derivation for the radius of electron orbits in an atom. It starts with the quantization condition relating to angular momentum and the centripetal force acting on an electron. By equating the electrostatic force to the centripetal force and applying mathematical manipulations, an expression for the radius of the electron's orbit is obtained. The video simplifies this expression to provide a shortcut formula for the radius of the nth shell in terms of the Planck's constant, the shell number, and the atomic number.
⚡ Calculating Electron Velocity and Energy
This section focuses on calculating the velocity and energy of an electron in the nth shell. The velocity formula is derived by substituting the radius expression into the angular momentum equation. The video then simplifies this to provide a shortcut formula for electron velocity. Similarly, the kinetic energy of an electron is derived and expressed in terms of the atomic number and shell number. The potential energy is discussed, with the video explaining why it is negative and how it relates to the kinetic energy.
🌠 Energy Levels and Transitions in Bohr's Model
The video explains the concept of energy levels in Bohr's model and how electrons can gain or lose energy by moving to higher or lower shells. It describes the process of excitation, where an electron gains energy and moves to a higher energy level, and de-excitation, where it loses energy and moves to a lower level. The quantization of energy is emphasized, stating that electrons can only gain or lose specific, quantized amounts of energy corresponding to the difference between two energy levels.
🔬 Bohr's Model and the Line Spectrum
The video concludes with how Bohr's model explains the line or discrete spectrum observed in atomic emissions, such as that of hydrogen. It connects the quantized energy levels to the specific frequencies of light emitted or absorbed during electron transitions. The formula for calculating the frequency of radiation during these transitions is introduced, and the video sets up the topic for further discussion in a subsequent video.
📚 Summary of Bohr's Atomic Model and Its Drawbacks
The final paragraph summarizes the development of atomic models, from Dalton's to Bohr's, and acknowledges that Bohr's model, despite its successes, also had its limitations. It invites viewers to research and discuss these drawbacks in the comments. The video ends with a prompt to like, subscribe, and follow Manoa Academy for more educational content.
Mindmap
Keywords
💡Atomic Model
💡Neils Bohr
💡Quantization
💡Electron Shells
💡Electrostatic Force
💡Angular Momentum
💡Energy Levels
💡Rutherford's Model
💡Planck's Constant
💡Spectral Lines
💡Excitation and De-excitation
Highlights
Niels Bohr challenged Albert Einstein and proposed the Bohr atomic model, which introduced the concept of electrons revolving in fixed orbits or shells around the nucleus.
The Bohr model postulates that electrons can only revolve in certain fixed orbits with specific energy levels, which was a departure from classical physics.
The quantization condition of the model states that the angular momentum of an electron in an orbit is an integer multiple of ħ (reduced Planck's constant).
Bohr's model explains the stability of atoms, which was a limitation in Rutherford's model, by suggesting that electrons in fixed orbits do not radiate energy.
The model also addresses the atomic spectrum, explaining why atoms emit or absorb light at specific wavelengths, which was not possible with previous models.
Bohr's model was able to calculate the energy levels of electrons in atoms, leading to the famous formula E_n = -13.6 eV / n^2 for the energy of an electron in the nth shell.
The model introduces the concept of excitation and de-excitation of electrons, which corresponds to the absorption and emission of energy, respectively.
The frequency of radiation absorbed or emitted during electron transitions can be calculated using the formula f = ΔE / ħ, where ΔE is the change in energy.
Bohr's model was the first to successfully explain the line spectrum of hydrogen, a series of discrete lines in the hydrogen emission spectrum.
The model suggests that the energy levels in an atom are quantized, meaning electrons can only occupy certain allowed energy levels.
The radius of an electron's orbit in the nth shell can be calculated using the formula r_n = n^2 * (0.529 Å) / Z, where Z is the atomic number.
The velocity of an electron in the nth shell can be determined by the formula v_n = 2.18 * 10^6 * Z / n, showing that velocity decreases as the shell number increases.
The kinetic energy of an electron in the nth shell is given by E_k = -13.6 eV * Z^2 / n^2, indicating that kinetic energy increases with higher shell numbers.
The potential energy of an electron in an atom is negative, reflecting the attractive force between the negatively charged electron and the positively charged nucleus.
The total energy of an electron in the nth shell is the sum of its kinetic and potential energies and is given by E_n = -3.4 * Z^2 / n^2 eV.
Bohr's model laid the foundation for quantum mechanics and was a significant step forward in understanding atomic structure and behavior.
Despite its successes, the Bohr model has limitations and could not accurately describe more complex atoms with multiple electrons.
The model's simplicity and visual appeal made it a cornerstone in the development of modern atomic theory and quantum mechanics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: