Gauss Law Problems - Infinite Sheet of Charge and Parallel Plate Capacitor - Physics
TLDRThis video script offers an in-depth exploration of calculating electric fields. It begins with the electric field produced by an infinite sheet of positive charge with a surface charge density of 60 nanocoulombs per square meter, using Gauss's Law to derive the formula. The script then shifts to the electric field between two parallel plates, illustrating how the field is generated by oppositely charged sheets and emphasizing its independence from distance due to the plates' large size. The final calculations for both scenarios are provided, highlighting the electric field's dependence on surface charge density and the permittivity of free space.
Takeaways
- 📚 The video focuses on calculating the electric field produced by an infinite sheet of charge and between two parallel plates.
- 🔍 Surface charge density is defined as the total charge divided by the area, measured in coulombs per square meter.
- 📐 Gauss's law is used to derive the formula for the electric field produced by an infinite sheet of charge.
- 🧲 The electric field produced by an infinite sheet of charge is independent of the distance from the sheet due to its infinite size.
- 📈 The electric field (E) from an infinite sheet of charge is calculated as the surface charge density (σ) divided by 2 times the permittivity of free space (ε₀).
- 🔢 For the given problem, the electric field is calculated using the formula E = σ / (2ε₀), resulting in 3390 newtons per coulomb.
- 🌐 The electric field between two oppositely charged parallel plates is considered, which is a scenario for a capacitor.
- 🔗 The electric field between the plates is the result of the combined effect of both charges, Q1 and Q2.
- 🚫 The electric field outside the plates is negligible, as it cancels out, especially for sufficiently large plates.
- 🔄 Gauss's law simplifies the calculation of the electric field between the plates to E = σ / ε₀, as the flux through the Gaussian surface is just E times the area (A).
- 🔑 The final electric field between the plates is calculated as approximately 1.69 x 10^6 newtons per coulomb using the given surface charge density of 15 micro coulombs per square meter.
Q & A
What is the focus of the video script?
-The video script focuses on calculating the electric field produced by an infinite sheet of charge and the electric field between two parallel plates, such as in a parallel plate capacitor.
What is the surface charge density given in the script?
-The surface charge density given in the script is 60 nanocoulombs per square meter.
How is surface charge density defined in the context of the script?
-In the script, surface charge density is defined as the total charge divided by the area.
What method is used to derive the formula for the electric field produced by an infinite sheet of charge?
-Gauss's law is used to derive the formula for the electric field produced by an infinite sheet of charge.
Why does the electric field produced by an infinite sheet of charge not depend on the distance from the sheet?
-The electric field does not depend on the distance because the sheet is so large that the effect of distance becomes negligible.
What is the formula derived for the electric field produced by an infinite sheet of charge?
-The formula derived for the electric field is E = σ / (2ε₀), where E is the electric field, σ is the surface charge density, and ε₀ is the vacuum permittivity.
What is the calculated electric field for the given surface charge density of 60 nanocoulombs per square meter?
-The calculated electric field for the given surface charge density is 3390 newtons per coulomb.
What is the situation described for the electric field between two oppositely charged sheets?
-The situation described is that of a capacitor, where the electric field is between two parallel plates with opposite charges, and the field outside the plates is negligible.
What is the formula for the electric field between two oppositely charged sheets or parallel plates?
-The formula for the electric field between two oppositely charged sheets is E = σ / ε₀.
What is the calculated electric field for the surface charge density of 15 microcoulombs per square meter?
-The calculated electric field for the surface charge density of 15 microcoulombs per square meter is approximately 1.69 x 10^6 newtons per coulomb.
How can the electric field be described in terms of the total charge on the surface?
-The electric field can be described as E = Q / (ε₀ * A), where Q is the total charge on the surface and A is the area of the plates.
Outlines
🔋 Calculating Electric Field of Infinite Charged Sheet
This paragraph discusses the calculation of the electric field produced by an infinite sheet of charge with a surface charge density of 60 nano coulombs per square meter. The explanation begins with the definition of surface charge density and proceeds to apply Gauss's law to derive the formula for the electric field. A visual aid, a cylinder, is used to demonstrate how the electric field lines exit in both directions, leading to an additive effect on the flux. The final formula obtained is E = σ / (2ε₀), where E is the electric field, σ is the surface charge density, and ε₀ is the vacuum permittivity. The calculation concludes with substituting the given values to find the electric field strength of 3390 newtons per coulomb, emphasizing that the field is independent of distance due to the sheet's infinite nature.
🔌 Electric Field Between Two Parallel Charged Plates
The second paragraph explores the electric field between two oppositely charged parallel plates, each with a surface charge density of 15 micro coulombs per square meter. The explanation involves drawing a visual representation and understanding that the electric field lines extend from the positive to the negative plate, with the field outside the plates being negligible. Focusing on the field between the plates, a Gaussian surface is used to apply Gauss's law, revealing that the electric field inside is a combination of the effects from both charges. The derived formula for the electric field between the plates is E = σ / ε₀. Substituting the given surface charge density into the formula yields an electric field strength of approximately 1.69 × 10^6 newtons per coulomb. The summary also touches on the relationship between surface charge density, total charge, and plate area.
📐 Deriving Electric Field Formula for Parallel Plate Capacitor
The final paragraph builds upon the previous discussion to derive the formula for the electric field in terms of the total charge on the surface of the plates. It reiterates that the electric field between the plates can be expressed as the charge divided by the product of ε₀ and the plate area (A). If the total charge (Q) is unknown, it can be found by multiplying the surface charge density (σ) by the plate area. This paragraph serves as a conclusion to the topic, reinforcing the understanding of how to calculate the electric field in a parallel plate capacitor configuration.
Mindmap
Keywords
💡Electric Field
💡Infinite Sheet of Charge
💡Surface Charge Density
💡Gauss's Law
💡Electric Flux
💡Permittivity of Free Space (Epsilon Sub Naught)
💡Parallel Plate Capacitor
💡Gaussian Cylinder
💡Outward Flux
💡Surface Charge Density Formula
💡Electric Field Calculation
Highlights
The video focuses on calculating the electric field produced by an infinite sheet of charge and between two parallel plates.
Surface charge density is defined as the total charge divided by the area.
Gauss's law is used to derive a formula for the electric field produced by an infinite sheet of charge.
A Gaussian cylinder is used to visualize the electric field exiting in both directions.
Electric flux is additive for outward fluxes from the positive charge.
Gauss's law states that electric flux equals the total charge enclosed by the Gaussian surface divided by epsilon naught.
The electric field produced by an infinite sheet is independent of the distance from the sheet due to its large size.
The formula for the electric field of an infinite sheet is derived as E = σ / (2ε₀).
Calculation example given for a surface charge density of 60 nanocoulombs per square meter.
Epsilon naught is given as 8.85 x 10^-12 C²/Nm², the unit for permittivity of free space.
The electric field between two oppositely charged sheets is calculated with a surface charge density of 15 microcoulombs per square meter.
The electric field outside the plates cancels out, being negligible.
The electric field inside the plates is the focus, as it's the situation of a capacitor.
The electric field between plates is derived as E = σ / ε₀.
The final answer for the electric field between plates is approximately 1.69 x 10^6 N/C.
The electric field can also be described in terms of the total charge on the surface.
The relationship between total charge, surface charge density, and area is explained.
Transcripts
Browse More Related Video

Capacitance | Circuits | Physics | Khan Academy
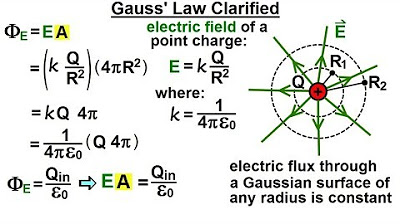
Physics 37.1 Gauss's Law Understood (4 of 29) Gauss' Law Clarified

4. Gauss's Law and Application to Conductors and Insulators
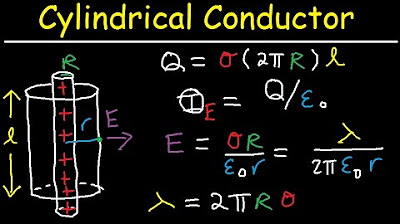
Gauss Law Problems, Cylindrical Conductor, Linear & Surface Charge Denisty, Electric Field & Flux,

Electric Field (1 of 3) An Explanation
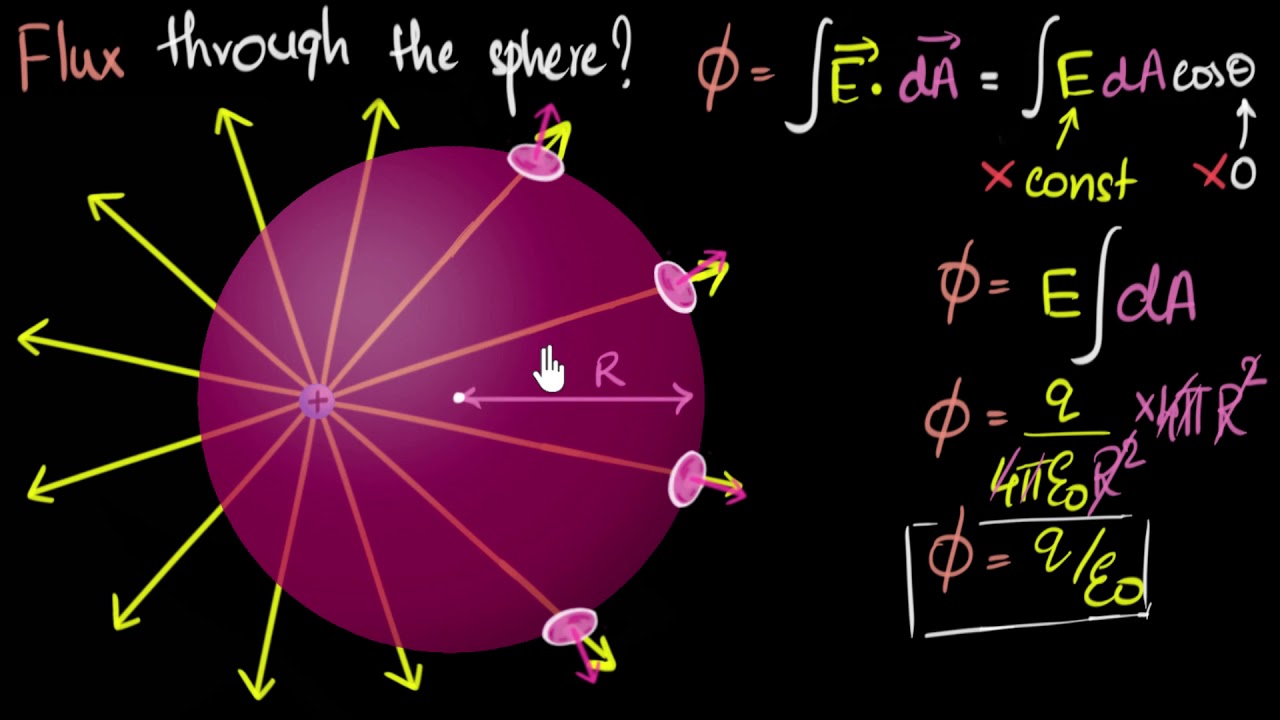
Gauss law of electricity | Electrostatics | Physics | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: