2. Electric Fields
TLDRThe video script is a detailed lecture on the principles of electromagnetism, specifically focusing on electric fields and forces. The professor begins by summarizing key points from a previous lecture, emphasizing the atomic structure, the concept of electric charge, and Coulomb's Law, which quantifies the electrostatic force between two charges. The lecture then delves into the calculation of electric fields due to multiple charges, highlighting the superposition principle that allows for the calculation of net forces. The professor also discusses the strong nuclear force that binds protons and neutrons within the atomic nucleus, despite the repulsive electrostatic force between protons. The script explores the visualization of electric fields with field lines, illustrating how they represent both the direction and magnitude of the field. It also touches on the limitations of Coulomb's Law when dealing with moving charges, as it violates the principles of special relativity. The concept of the electric field as a distinct entity that charges respond to is introduced, and the script concludes with the calculation of the force and torque experienced by a dipole in a uniform electric field. The potential energy of a dipole in an electric field is also derived, highlighting the dipole's tendency to align with the field due to torque. The lecture is rich with mathematical derivations and physical insights, providing a comprehensive understanding of electric fields and their interactions with charges.
Takeaways
- 📚 The fundamental concept that everything is made of atoms, which consist of a nucleus containing protons and neutrons, and electrons orbiting outside.
- ⚡ The significance of electric charge (q) where neutrons have no charge (q=0), electrons have a negative charge (q=-1.6x10^-19 C), and protons have a positive charge, with interactions between charges following Coulomb's Law.
- 🔧 The principle of superposition allows for the calculation of forces in systems with multiple charges, as the interaction between pairs of charges is independent of other charges present.
- ⚖️ The immense difference in magnitude between gravitational and electric forces, with the electric force being approximately 10^-40 times stronger, as derived from the force between an electron and a proton.
- 🧲 The strong nuclear force, which is even stronger than the electric force, is responsible for holding protons together in the nucleus despite their mutual repulsion.
- 💥 The realization that while the electric force is strong, it has a longer range compared to the nuclear force, which is short-range but dominant at the subatomic level.
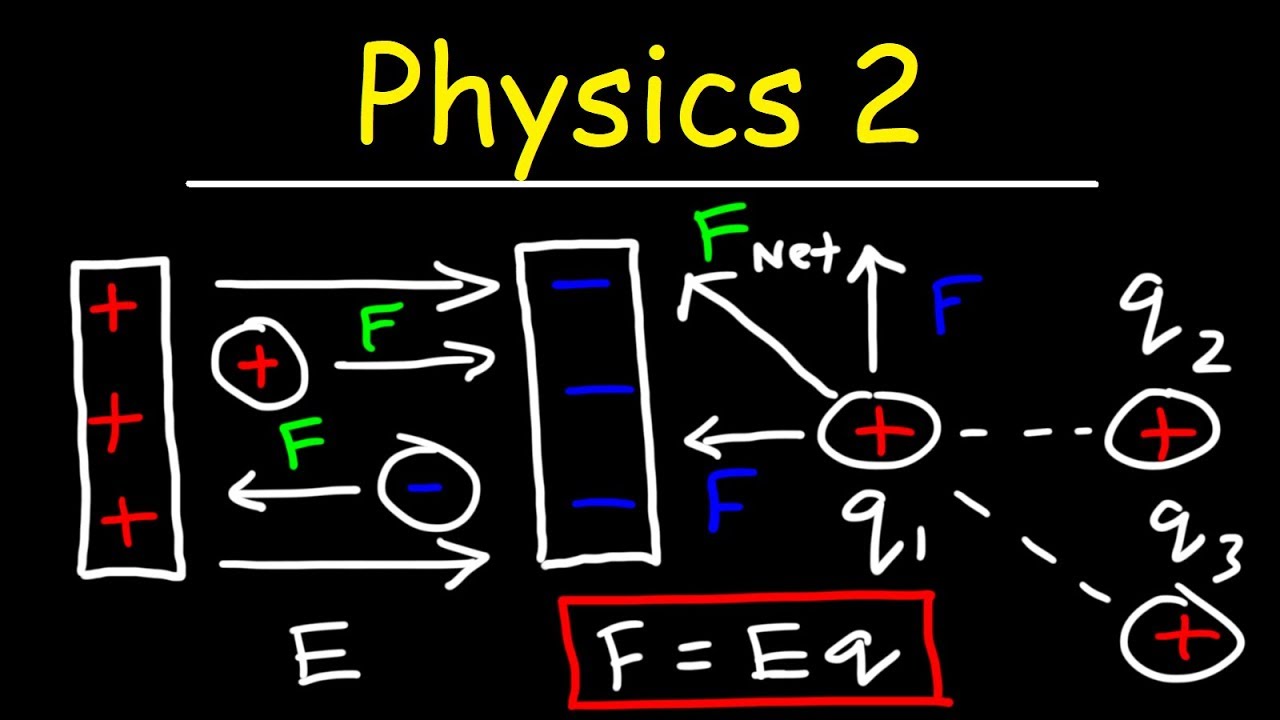
- 🌌 The concept of the electric field, which is produced by charges and can be calculated for any point in space, allowing for the understanding of force on a charge placed at that point.
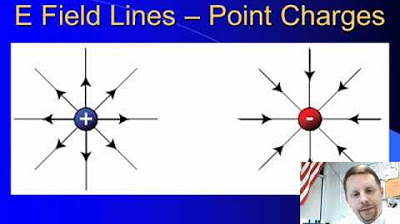
- 📈 The use of field lines to visually represent the electric field, where the density of the lines indicates the field's strength, and the lines' direction indicates the field's direction at that point.
- 🚫 The limitation of Coulomb's Law when charges are in motion, as it does not account for the time it takes for the force's effect to propagate, which is essential in the context of special relativity.
- 🤔 The calculation of the electric field due to a dipole (two equal and opposite charges), which at large distances falls off with the inverse cube of the distance (1/r^3), as opposed to the inverse square (1/r^2) for a single charge.
- ⚙️ The impact of an external electric field on a dipole, which experiences a torque and potential energy that depend on the angle between the field direction and the dipole moment, with the potential energy given by -p⋅E.
Q & A
What are the fundamental components of an atom?
-An atom is made up of a nucleus, which contains protons and neutrons, and electrons that orbit outside the nucleus.
What property do entities with electric charge possess?
-Entities with electric charge have the ability to interact with other entities that also possess electric charge.
What is the unit of electric charge?
-The unit of electric charge is the coulomb.
How does the force between two charged entities vary with distance?
-The force between two charged entities varies inversely with the square of the distance between them, as described by Coulomb's Law.
What is the superposition principle in the context of electric charges?
-The superposition principle states that the total electric force on a charge is the vector sum of the forces from all the individual charges, allowing for the calculation of forces in complex systems with multiple charges.
Why do protons stay together in the nucleus despite their mutual repulsion?
-Protons stay together in the nucleus due to the strong nuclear force, which is stronger than the repulsive electric force at the small distances found within the nucleus.
What is the difference between the range of the nuclear force and the electric force?
-The nuclear force is a short-range force, becoming negligible over larger distances, whereas the electric force, while stronger at a distance, falls off more slowly and can be significant over larger distances.
How does the electric field concept help in understanding the interaction of charges over time and space?
-The electric field concept allows us to understand that a charge produces a field that exists everywhere in space and evolves over time, taking into account the past positions and movements of charges due to the finite speed of light.
Why is Coulomb's Law not suitable for calculating the force between moving charges?
-Coulomb's Law is not suitable for moving charges because it implies an instantaneous interaction between charges, which violates the principles of special relativity that forbids faster-than-light communication.
What is the dipole moment and how is it related to the electric field produced by a pair of equal and opposite charges?
-The dipole moment is a vector quantity that represents the product of the separation between two charges and the charge magnitude. It determines the electric field's behavior at locations far from the charges, where the field varies as the inverse cube of the distance and is parallel to the dipole moment.
How does the potential energy of a dipole in an electric field relate to its orientation?
-The potential energy of a dipole in an electric field is given by -p dot E, where p is the dipole moment and E is the electric field. The potential energy is lowest when the dipole is aligned with the field and highest when it is anti-parallel, indicating a stable and unstable equilibrium, respectively.
Outlines
😀 Introduction and Summary of Last Lecture
The professor begins by acknowledging the large class size and decides against asking if everyone followed the previous lecture. Instead, they provide a quick summary of the key points: the atomic structure, electric charge, and Coulomb's Law for calculating the force between two charges. The importance of the superposition principle is emphasized for understanding interactions among multiple charges. The correction of a student's suggestion regarding the force law is highlighted, and the professor encourages students to actively participate in correcting any errors.
🧲 The Strong Nuclear Force and Coulomb's Law
The discussion shifts to the strong nuclear force that keeps protons together in a nucleus despite their mutual repulsion through Coulomb's Law. The professor emphasizes that this force is much stronger than the electric force but has a very short range. The difference in the range of the nuclear force and the electric force is explained, with the latter dominating at larger distances due to its inverse-square falloff with distance.
🚀 The Concept of Electric Field
The concept of the electric field is introduced as a way to calculate the force on a charge without needing a second charge. The electric field is presented as a vector quantity that can be defined everywhere in space, and its relationship with the force on a charge is established. The idea of a test charge is used to explain how the electric field can be measured and how it is influenced by all the charges in the vicinity.
📐 Visualizing Electric Fields with Field Lines
The professor explains how to visualize electric fields using field lines, which represent both the direction and the strength of the field. The density of these lines is proportional to the strength of the electric field, and they are drawn according to a convention that ensures the number of lines per unit area is equal to the field's magnitude. The visualization method is applied to various charge configurations, including single charges, dipoles, and parallel plate capacitors.
📐 Mathematical Calculation of Electric Field
The professor provides a mathematical approach to calculating the electric field due to a dipole at specific points along its axis and perpendicular to the axis. The calculation involves vector addition and the use of dipole moment, which is defined as the product of the charge and the separation distance between the charges. The resulting formulas are derived for points close to and far from the dipole.
🤔 Interaction of Dipoles with Electric Fields
The response of a dipole placed in a uniform electric field is explored. While the net force on the dipole is zero due to equal and opposite charges, a torque is present that tends to align the dipole with the field. The torque and the associated potential energy of the dipole in the field are calculated, and the conditions for stable and unstable equilibria are discussed. The potential energy is shown to be dependent on the angle between the dipole moment and the electric field.
📝 Summary of Key Concepts
The lecture concludes with a summary of the main points: the shift from considering direct interactions between charges to thinking in terms of electric fields, the method for calculating the electric field due to various charge configurations, the use of field lines for visualizing electric fields, and the behavior of a dipole in an electric field, including the calculation of torque and potential energy. The importance of these concepts for future topics in the course is emphasized.
Mindmap
Keywords
💡Atomic Structure
💡Electric Charge
💡Coulomb's Law
💡Superposition Principle
💡Nuclear Force
💡Electric Field
💡Field Lines
💡Dipole Moment
💡Torque
💡Potential Energy
💡Special Theory of Relativity
Highlights
The atomic structure is composed of a nucleus with protons and neutrons, and electrons orbiting outside.
Electric charge is a property denoted by 'q', with different entities having specific charge values.
Coulomb's Law describes the force between two charges and is fundamental to understanding electromagnetic interactions.
The superposition principle allows for the calculation of forces in systems with multiple charges.
Gravitational force is significantly weaker than electric force, with a ratio around 10 to the -40th power.
The strong nuclear force is stronger than the electric force and is responsible for holding protons together in a nucleus.
The range of a force is crucial in determining its impact, with the nuclear force being short-ranged compared to the electric force.
Coulomb's Law is applicable for static charges but not suitable for moving charges due to the limitations of instantaneous communication.
The electric field is a concept that allows for the calculation of forces on charges without the need for a second charge.
The density of electric field lines is proportional to the strength of the field, providing a visual representation of the field's intensity.
The electric field due to a single charge follows an inverse square law, represented by the formula q/(4πε₀r²).
The dipole moment (p) is a vector quantity that describes the charge distribution in a dipole and is crucial for calculating the field.
The potential energy of a dipole in an electric field is given by -p dot E, which indicates the work done against the field.
The torque on a dipole in an electric field is p cross E, which tends to align the dipole with the field direction.
The concept of stable and unstable equilibrium is illustrated by the behavior of a dipole in an electric field.
The importance of active participation and anticipation during lectures to ensure understanding and catch potential errors.
The use of electric fields to manipulate electron beams is fundamental to the operation of television screens.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: