6. Capacitors
TLDRThe transcript is a detailed lecture on electrostatics, covering the concept of electric potential, its relation to the electric field, and the calculation of potential energy. The professor begins by reviewing the mathematical foundation established in the previous class, emphasizing the importance of understanding electric fields as conservative forces. The potential is introduced as a way to simplify calculations, particularly for determining the work done by the electric field. The lecture then delves into the relationship between charge, potential, and energy, highlighting the principle of superposition and the method for calculating the potential due to multiple charges. The professor also corrects a previous mistake regarding the proof of the conservative nature of the electric field, using a triangle example to illustrate the error. Units for electric field and potential are discussed, with an emphasis on their importance in calculations. The advantages of using potential, including energy conservation, simplified computation of electric fields, and the ability to visualize electric fields, are explored. The lecture concludes with a discussion on the behavior of conductors in electric fields, the concept of capacitance, and the energy stored in a capacitor. The professor uses various analogies, such as a jellyfish and a roller coaster, to explain complex concepts in an accessible manner.
Takeaways
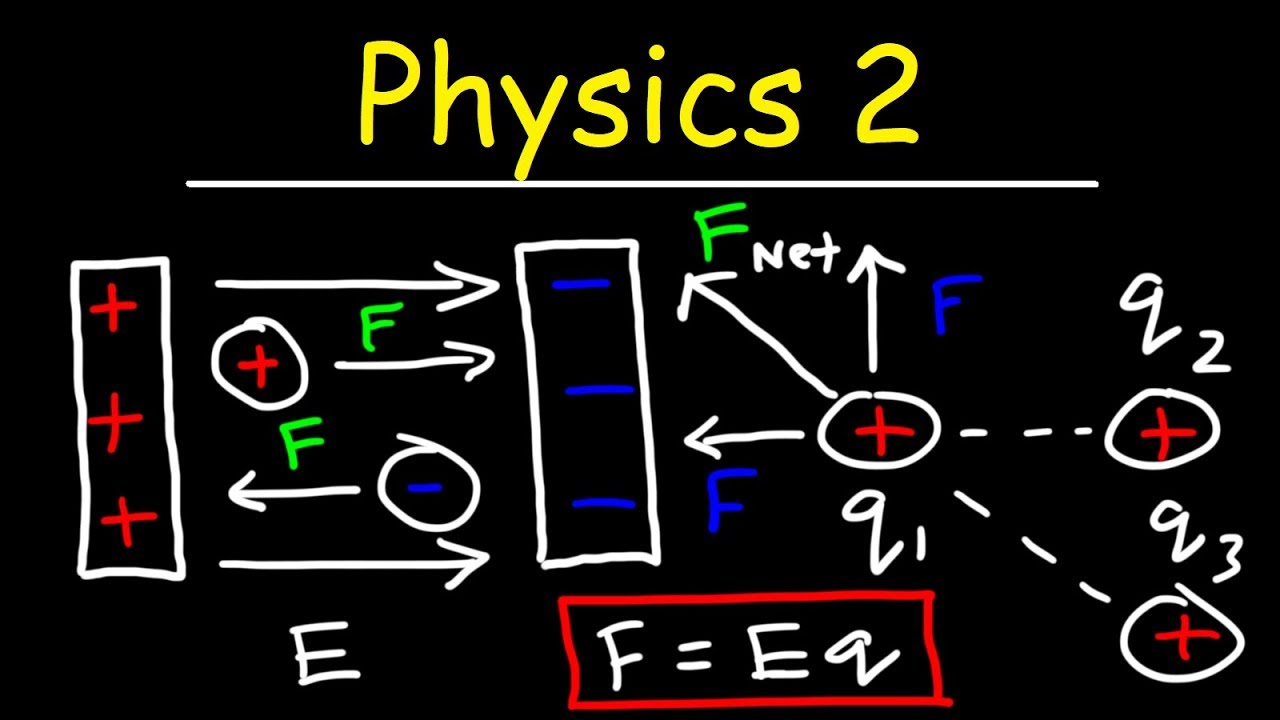
- 📚 The electric field, understood as Coulomb's forces, allows for the definition of potential because it is a conservative force, meaning the integral of the electric field over any closed loop is zero.
- 🔋 The potential energy in an electric field is given by q times V, where q is the charge and V is the potential, similar to how potential energy in gravity is mgh, with m being mass, g the acceleration due to gravity, and h the height.
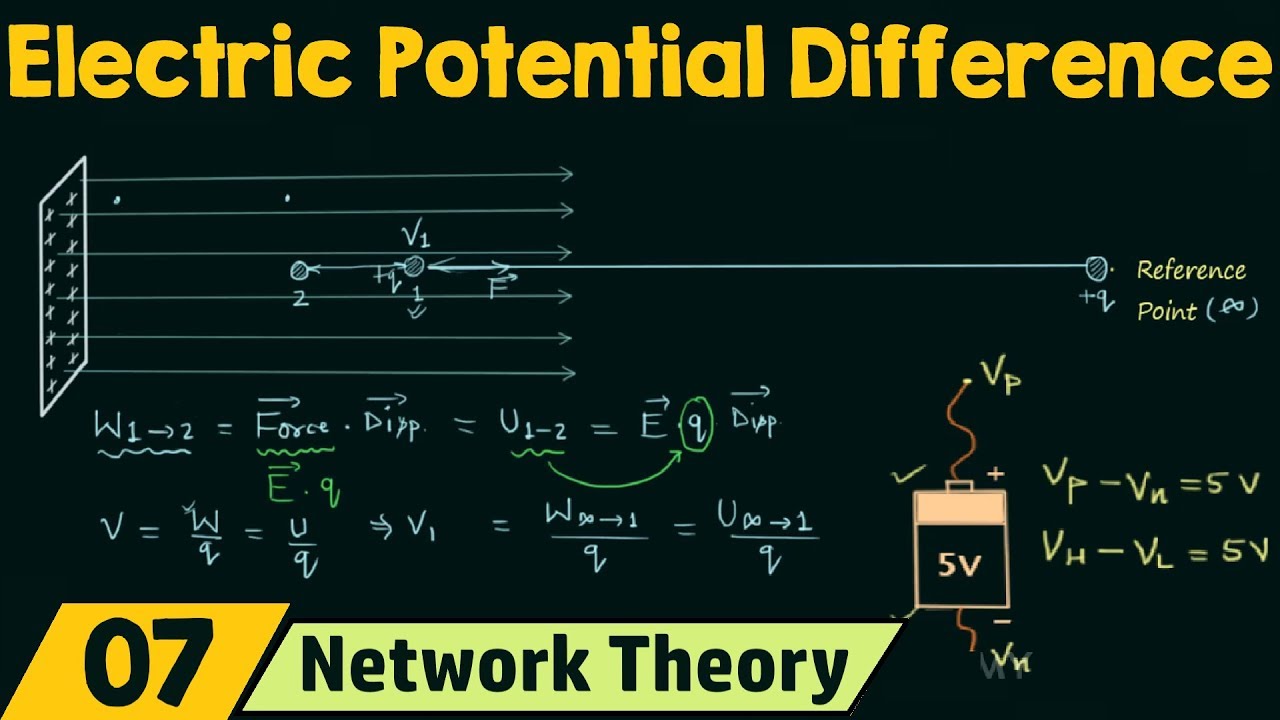
- 🧮 The general formula for electric potential V is the line integral of E⋅dr from one point to another, where E is the electric field and dr is the displacement vector.
- 🌐 For a single charge, the potential V at a point in space is given by q/4Πε_0 times r, where r is the distance from the charge, and ε_0 is the vacuum permittivity.
- 🔧 The work done against the electric field to move a charge from one point to another is equal to the change in potential energy, which can be calculated using the potential difference and the charge.
- 🚫 The professor admitted a mistake in a previous lecture regarding the proof of the electric field being conservative, emphasizing the importance of accurate path work calculations.
- 📈 The potential difference between two points in an electric field is independent of the path taken due to the conservative nature of the electric field.
- 📊 Units are crucial in physics problems, as they ensure the correctness of the calculations and help in keeping track of the calculations' progress.
- 💡 The advantages of using electric potential V include conservation of energy, ease of computing the electric field E by taking derivatives of V, and providing intuitive visual representations of the electric field landscape.
- 🔏 For a conductor in an electric field, the internal electric field is zero, and any excess charge resides on the surface. A conductor is an equipotential body, meaning the potential is the same throughout its entirety.
- 🔵 The electric field lines are always perpendicular to lines of constant potential (equipotentials), which is a general result and not limited to cases with high symmetry.
Q & A
What is the significance of the electric field being a conservative force?
-The electric field being a conservative force means that the work done in moving a charge around a closed path is zero. This property allows us to define a potential, which is a scalar quantity that represents the work done per unit charge in moving a test charge from a reference point to a specific point within the field without necessarily following a specific path.
Why is the potential difference associated with the work done by the electric field?
-The potential difference is associated with the work done by the electric field because it represents the work required to move a unit charge against the electric field from one point to another. This work done per unit charge is what defines the potential at a point in the field.
How is the electric potential energy related to the potential and the charge?
-The electric potential energy (U) is related to the potential (V) and the charge (q) by the formula U = q * V. It represents the work done against the electric field when assembling a charge distribution and is the energy that a charge has due to its position in an electric field.
What is the principle of superposition in the context of electric potential?
-The principle of superposition states that the total potential at a point due to multiple charges is the sum of the potentials due to individual charges at that point. This principle is applicable because electric fields (and thus potentials) are linear and can be summed directly.
Why is it easier to compute the electric field from the potential rather than the other way around?
-Computing the electric field from the potential is easier because the potential is a scalar quantity, and to find the field, you simply take the gradient (or derivative) of the potential. On the other hand, finding the potential from the field involves integrating the field over a path, which is a more complex operation, especially when dealing with vector quantities.
How does the electric field provide a visual landscape for understanding electric potential?
-The electric field lines can be thought of as the contours or 'steps' of an electric potential 'landscape'. The direction of the field lines indicates the direction of the steepest increase in potential, and the spacing between the lines indicates the magnitude of the field. This visual representation helps in understanding how charges move within the field and the work done in moving them.
What is the relationship between the lines of constant potential (equipotentials) and the electric field lines?
-The lines of constant potential, or equipotentials, are always perpendicular to the electric field lines. This is because the electric field is defined as the negative gradient of the potential, and the gradient points in the direction of the steepest increase in potential, which means that moving along an equipotential (where the potential does not change) is perpendicular to the field.
How does the electric field behave inside a conductor?
-Inside a conductor, the electric field is zero. This is because free electrons within the conductor move until they cancel out any internal electric field, ensuring that the conductor is an equipotential body. This movement of charges redistributes the charge on the surface of the conductor to achieve this zero field condition.
What is the significance of the electric potential being constant on a conductor?
-The constant electric potential on a conductor is significant because it implies that no work is done when moving a charge along the surface of the conductor. This is due to the absence of an electric field within the conductor, which allows for the easy manipulation and understanding of charge distributions on the conductor's surface.
How does the energy stored in a capacitor relate to the charge and voltage across its plates?
-The energy stored in a capacitor (U) is related to the charge (Q) and the voltage (V) across its plates by the formula U = ½QV or U = ½CV^2, where C is the capacitance. This energy is the work done to charge the capacitor and is recoverable when the capacitor discharges.
What is the capacitance of a parallel plate capacitor and how is it determined?
-The capacitance of a parallel plate capacitor is determined by the formula C = ε₀A/d, where ε₀ is the vacuum permittivity, A is the area of the plates, and d is the distance between the plates. This formula is derived from the ability of the system to store charge, which is proportional to the charge Q and inversely proportional to the voltage V across the plates.
Outlines
😀 Introduction to Electric Potential and Fields
The professor begins by recapping the previous lecture's focus on mathematical details related to electric fields and potential. He emphasizes the importance of understanding electric fields as conservative forces, which allows for the definition of electric potential. The potential energy is discussed in analogy to gravitational potential energy, highlighting that the actual energy involves the charge times the potential (qV). The concept of potential as electrical height is introduced, and the formula for potential difference is given as the line integral of the electric field E dot dr from one point to another.
📡 Electric Potential due to Multiple Charges
The paragraph delves into calculating the electric potential due to multiple charges, using the principle of superposition. It is explained that the potential V at a point in space due to multiple charges is the sum of the potentials due to each individual charge, calculated as q/(4πε₀r), where q is the charge and r is the distance from the charge to the point. The potential difference is obtained by integrating the electric field, and the electric field E is derived from the potential through its gradient, which involves partial derivatives with respect to x and y components.
🔍 Correcting Mistakes on Electric Field Path Integrals
The professor acknowledges a mistake made in a previous explanation regarding the electric field's path integrals. He clarifies that approximating a smooth path by radial and angular segments for integral calculation can be misleading. Using the example of a triangle, he demonstrates that even if two paths are similar, the work done (and thus the path length) can differ, emphasizing the need for accuracy when deforming paths in integral calculations.
🔋 Units and Tenure: A Humorous Aside
The professor discusses the importance of using units in physics calculations, stating that without them, the numerical results are meaningless. He humorously contrasts the meticulous approach of students with the perceived laxity that comes with academic tenure, using the analogy of a jellyfish's sedentary lifestyle to describe the perks of being a tenured professor.
🚀 Advantages of Electric Potential in Physics Problems
The professor outlines the advantages of using electric potential (V) in physics problems. These include the conservation of energy, which simplifies calculations involving work and energy transfers; the ease of computing the electric field (E) from the potential through derivatives; and the ability to visualize physical scenarios, such as electric fields between charged plates, more intuitively.
📚 Calculation Techniques for Electric Fields and Potentials
The paragraph focuses on methods for calculating electric fields and potentials. It discusses how to compute the potential at a point due to a charge distribution, such as a ring of charge, by integrating the contributions from infinitesimally small charges. The text also highlights an example where it is easier to determine the electric field first and then integrate it to find the potential, such as with a hollow conducting sphere.
🧲 Electric Potential and Fields in Conductors
The professor discusses the behavior of electric fields and potentials in conductors. He explains that a conductor in an external electric field will induce charges on its surface that create an internal electric field to counteract the external field, resulting in a zero net electric field inside the conductor. The text also explores the concept that the interior of a hollow conductor is an equipotential surface, meaning the potential is constant throughout the interior.
🔌 Capacitors and Energy Storage in Electrostatics
The final paragraph introduces capacitors as devices for storing electrical charge and energy. It explains the concept of capacitance, which is the ability of a system to store charge per unit voltage. The professor derives the formula for capacitance in terms of the geometry of a parallel plate capacitor and discusses how to calculate the energy stored in a capacitor, which can be expressed either in terms of the charge or the voltage across the plates.
Mindmap
Keywords
💡Electric Field
💡Potential Energy
💡Coulomb's Law
💡Conservative Force
💡Line Integral
💡Potential Difference
💡Gradient
💡Principle of Superposition
💡Equipotential Surfaces
💡Capacitance
💡Energy Stored in a Capacitor
Highlights
The electric field, understood as Coulomb's forces, allows defining a potential due to its conservative nature.
The force on a charge is not just the electric field but the charge times the electric field, emphasizing the role of the charge in potential energy.
The potential difference is associated with the work done by the electric field times the charge, highlighting the concept of potential energy as q times V.
The principle of superposition is explained for calculating the potential due to multiple charges, which is a sum over all charges.
The gradient of the potential gives the electric field, demonstrating the relationship between potential and field through derivatives.
A correction is made regarding the proof of the electric field being conservative, emphasizing the importance of accurate mathematical reasoning.
The units of electric field and potential are discussed, providing clarity on their physical meanings and implications.
The advantages of using potential in electrostatics are outlined, including conservation of energy, ease of computing electric fields, and visual intuitiveness.
The electric potential landscape is likened to a gravitational field, providing a visual aid for understanding potential differences and electric fields.
Equipotentials are shown to be perpendicular to electric field lines, a general result derived from the relationship between potential change and field direction.
The behavior of charges within a conductor is explained, including how they distribute on the surface and the concept that the interior of a conductor is an equipotential.
The method of using an infinite conducting plane as an image charge to solve electrostatic problems is introduced, offering a clever approach to complex calculations.
The work required to assemble a collection of charges is calculated, providing insight into the energy involved in building up charge configurations.
The concept of capacitance is introduced as a measure of a system's ability to store charge, defined as the charge transferred divided by the voltage difference.
The capacitance of a parallel plate capacitor is derived, showing a simple calculation based on the geometry and properties of the plates.
The energy stored in a capacitor is calculated, demonstrating the relationship between charge, voltage, and energy in the context of a capacitor.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: