Physics 2 - Basic Introduction
TLDRThe video delves into key concepts of second-semester physics, focusing on electric charges, forces, and fields. It explains how like charges repel and opposite charges attract, quantified by Coulomb's Law. The script explores the effects of varying charge magnitudes and distances on electrostatic forces, introducing the concept of electric field and potential. It further discusses the work done by electric fields on charges and the relationship between electric potential energy, electric potential, and voltage, clarifying the differences and their significance in physics.
Takeaways
- 🔋 Understanding Electric Charges: Like charges repel each other while opposite charges attract, following Coulomb's Law, which quantifies the electrostatic force between charges.
- 📈 Coulomb's Law Formula: The force (F) between two charges (q1 and q2) is given by k*q1*q2/r^2, where k is Coulomb's constant, and r is the distance between the charges.
- 🔄 Effect of Changing Charges: Doubling the magnitude of either charge (q1 or q2) doubles the force between them, while doubling both charges quadruples the force.
- 📊 Impact of Distance on Force: Increasing the distance between charges reduces the force between them. If the distance is doubled, the force becomes one-fourth of its original value.
- 🔧 Calculating Electrostatic Force: Given specific values for charges and distance, the magnitude of the force between them can be calculated using Coulomb's Law.
- 🌐 Direction of Electric Forces: The direction of the force on a charge depends on the sign of the charge and the configuration of other charges. Opposite charges attract, while like charges repel.
- 🔋 Electric Charge and Protons/Electrons: The sign of the electric charge indicates the relative number of protons and electrons. A positive charge means more protons than electrons, while a negative charge indicates more electrons than protons.
- 📐 Electric Field: The electric field (E) is defined as the force exerted on a positive test charge divided by the magnitude of that test charge.
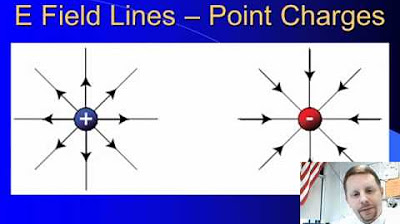
- 🎯 Direction of Electric Field: The direction of the electric field at a point is determined by the configuration of charges. Positive charges create an electric field that radiates outward, while negative charges create an electric field that points inwards.
- ⚖️ Work Done by Electric Fields: The work done by an electric field on a charge depends on the direction of the force relative to the charge's displacement. Positive work indicates an increase in kinetic energy and a decrease in potential energy, while negative work indicates the opposite.
- 🔌 Electric Potential: Electric potential (V) is the ratio of electric potential energy to charge and is measured in volts (V). It represents the potential for doing work per unit charge in an electric field.
Q & A
What is the basic concept of electric charge and how do like and opposite charges interact?
-Electric charge is a fundamental property of matter that gives rise to one of the four fundamental forces of nature, the electromagnetic force. Like charges, such as two positive charges, repel each other, while opposite charges, like a positive and a negative charge, attract each other. This interaction is described by Coulomb's Law, which quantifies the electrostatic force between charges.
What is Coulomb's Law and how does it relate to the force between two charges?
-Coulomb's Law states that the electric force between two point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. Mathematically, it is represented as F = k * (q1 * q2) / r^2, where F is the force, k is Coulomb's constant, q1 and q2 are the charges, and r is the distance between the charges. This law helps in quantifying the magnitude of the force between two charges.
How does increasing the magnitude of charges affect the electrostatic force between them?
-If the magnitude of one or both charges is increased, the electrostatic force between them also increases. Specifically, if one charge is doubled, the force is doubled; if both charges are doubled, the force increases by a factor of four (2 * 2 = 4). This is because the force is proportional to the product of the charges.
What happens to the electrostatic force when the distance between two charges is increased?
-When the distance between two charges is increased, the electrostatic force acting on them decreases. This is because the force is inversely proportional to the square of the distance (r^2). If the distance is doubled, the force becomes one-fourth of its original value, as per Coulomb's Law.
How can you calculate the magnitude of the force between two charges using Coulomb's Law?
-To calculate the force between two charges using Coulomb's Law (F = k * (q1 * q2) / r^2), you need to know the values of the charges (q1 and q2) in coulombs, the distance (r) between them in meters, and the value of Coulomb's constant (k), which is 9 * 10^9 N m^2/C^2. Plug these values into the formula and solve for F to get the force in newtons.
What is the significance of the electric field and how is it defined?
-The electric field is a region around a charged particle where an electric force is exerted on other charged particles. It is defined as the force experienced by a positive test charge divided by the magnitude of that test charge. The electric field gives a measure of the force that would be experienced by a charge placed in the field and its direction indicates the direction in which a positive test charge would be pushed or a negative test charge would be pulled.
How does the direction of the electric field affect the force experienced by positive and negative charges?
-The direction of the electric field is the same as the direction in which a positive charge would experience a force and opposite to the direction in which a negative charge would experience a force. A positive charge will experience a force in the same direction as the electric field, while a negative charge will experience a force in the opposite direction. This is because electric fields originate from positive charges and terminate at negative charges.
What is electric potential and how is it related to electric potential energy?
-Electric potential, denoted by the symbol V, is the ratio of the electric potential energy (EPE) of a charge to the magnitude of that charge. It is a measure of the potential energy per unit charge at a point in an electric field. The unit for electric potential is the volt (V), where one volt is equal to one joule of potential energy per coulomb of charge. Electric potential energy (PE) is the energy a charge possesses due to its position in an electric field, and it can be converted to other forms of energy.
How does the work done by an electric field on a charge affect its kinetic and potential energy?
-When a charge moves through an electric field, the electric field can do work on it. If the work done is positive, the charge's kinetic energy increases while its potential energy decreases because the charge is moving in the direction of the electric field. Conversely, if the work done is negative, the charge's kinetic energy decreases and its potential energy increases because the charge is moving against the direction of the electric field.
What is the relationship between electric potential difference and the work done on a charge?
-The work done on a charge as it moves from one point to another in an electric field is directly related to the electric potential difference (ΔV) between those points. The work (W) done is given by the equation W = -q * ΔV, where q is the charge and ΔV is the potential difference (Va - Vb). The negative sign indicates that if the charge moves from a higher potential to a lower potential, the work done is positive (energy is gained), and if it moves from a lower potential to a higher potential, the work done is negative (energy is lost).
How can you determine the net electric force and field acting on a charge in a situation with multiple charges?
-To determine the net electric force or field on a charge in the presence of multiple charges, you calculate the individual forces or fields exerted by each charge on the charge of interest. Then, you vectorially add these individual forces or fields to find the resultant net force or field. The direction of the net force or field is the direction of the resultant vector after adding all the individual vectors.
What is the significance of electric potential in the context of a charged parallel plate capacitor?
-In the context of a charged parallel plate capacitor, the electric potential difference between the plates establishes an electric field between them. This field stores electric potential energy, which can do work on charges moving within the field. The potential difference is directly related to the amount of charge stored on the plates and the distance between them. The potential difference can be used to calculate the work done on a charge when it moves from one plate to the other.
Outlines
📚 Introduction to Electrostatics and Coulomb's Law
This paragraph introduces the concepts typically taught in the second semester of physics, focusing on electric charges and their interactions. It explains how like charges repel each other, while opposite charges attract, using Coulomb's Law as a quantitative tool. The law states that the electric force between two charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. The constant 'k' in the equation represents the electrostatic force constant, and the units are newtons times square meters per coulomb squared. The explanation includes the impact of increasing the magnitude of charges and the distance between them on the force, emphasizing the relationship between proximity and strength of the electrostatic force.
🔋 Understanding the Effects of Charge Magnitude and Distance on Electrostatic Force
This section delves deeper into how changing the magnitude of charges and the distance between them affects the electrostatic force. It uses a hypothetical scenario where a positive and a negative charge are separated by a certain distance, and the force acting on each charge is calculated. The paragraph explains what happens when the charges are brought closer together or when the magnitude of the charges is increased. By using Coulomb's Law, the explanation shows how the force can be calculated in different scenarios, highlighting the mathematical approach to solving such problems and the proportionality factors involved.
🔧 Calculating Electrostatic Force with Given Charge Magnitudes and Distances
This paragraph presents a practical problem-solving approach to calculating the electrostatic force between two charges with given magnitudes and separation distances. It uses specific values for the charges in microcoulombs and the distance in centimeters, guiding the viewer through the process of converting units and applying Coulomb's Law. The summary emphasizes the importance of understanding the direction of the force and the nature of the charges (attraction for opposite charges and repulsion for like charges), as well as the calculation of the electrostatic force in newtons based on the given parameters.
💡 Exploring the Concept of Electric Charge and its Quantification
This section provides a foundational understanding of electric charge, explaining its representation and what it signifies. It distinguishes between positive and negative charges based on the presence of more protons or electrons, respectively. The paragraph details how to calculate the equivalent number of protons or electrons for a given charge magnitude, using the charge of a single electron or proton as a conversion factor. It also explains how to determine the net charge in an object by comparing the number of protons to electrons, which is crucial for understanding electric forces and fields.
🧭 Determining the Direction of Electric Forces in Multiple Charge Scenarios
This paragraph discusses the direction of the net electric force acting on charges in more complex scenarios involving multiple charges. It explains how to determine the resultant force direction when charges are equally spaced and have the same magnitude. The explanation includes a visual representation of the forces as vectors and how they combine to form a resultant force, indicating the general direction the charge will experience. The concept is further clarified with examples of positive and negative charges and their interactions in the electric field they create.
🌐 Understanding Electric Fields and their Relationship with Charges
This section introduces the concept of the electric field, defined as the force exerted on a positive test charge divided by the magnitude of that test charge. It explains how to calculate the electric field at a point in space and how the electric field changes with the magnitude of the charge and the distance from the charge. The explanation includes the direction of electric fields around positive and negative charges and how they influence the force experienced by other charges placed in the field. The paragraph also discusses the relationship between electric fields and the forces they exert on charges, emphasizing the importance of understanding this concept for further studies in electricity.
🔄 Analyzing the Electric Field created by Multiple Charges
This paragraph explores the electric field at various points in the presence of multiple charges, both positive and negative. It explains how to determine the direction of the electric field at specific points by considering the contributions from each charge. The explanation includes the process of vector addition to find the net electric field and how the relative strengths and directions of the electric fields from individual charges affect the overall field. The paragraph also discusses the concept of every charge creating its own electric field and how these fields叠加 to determine the resultant field at a point.
💫 Electric Potential Energy and its Transformation into Kinetic Energy
This section discusses the relationship between electric potential energy, kinetic energy, and the work done by electric fields on charges. It explains how the work done by the electric field on a charge can be positive or negative, depending on the direction of the force relative to the charge's displacement. The explanation includes scenarios where a charge moves from a region of high potential energy to low potential energy, and vice versa, illustrating how this affects the charge's kinetic and potential energy. The paragraph emphasizes the connection between the work-energy principle and the behavior of charges in electric fields.
🔌 Electric Potential and its Measurement
This paragraph defines electric potential as the ratio of electric potential energy to charge and explains its unit as volts. It clarifies that electric potential is an arbitrary value and only meaningful when comparing different points in an electric field. The explanation includes how the difference in electric potential, or voltage, is what can be measured and how it relates to the work done on a charge as it moves through an electric field. The paragraph also introduces the concept of electric potential energy and its relationship with electric potential, emphasizing the importance of understanding these concepts for a comprehensive grasp of electricity.
⚡️ Work Done by Electric Forces and its Relation to Electric Potential Difference
This section explains the work done by electric forces on charges as they move through an electric field and how it relates to the electric potential difference. It describes the formula for work done as negative charge times the electric potential difference and provides examples of how this works for positive and negative charges moving between points with different potentials. The explanation includes the calculation of work done on a charge and how it corresponds to changes in electric potential energy and kinetic energy, reinforcing the understanding of how energy is transformed in electric fields.
Mindmap
Keywords
💡Charges
💡Coulomb's Law
💡Electric Field
💡Electric Potential
💡Work
💡Kinetic Energy
💡Potential Energy
💡Vector
💡Ohm's Law
💡Capacitors
💡Electric Potential Difference
Highlights
Introduction to common concepts taught in the second semester of physics, focusing on electric charges and their interactions.
Explanation of how like charges repel each other, such as two positive charges, while opposite charges attract each other, like a positive and a negative charge.
Quantification of the force between two charges using Coulomb's Law, expressed as F = k * q1 * q2 / r^2, where k is a constant, q1 and q2 are the charges, and r is the distance between them.
Discussion on the effect of increasing the magnitude of charges on the electrostatic force between them, noting that if one charge is doubled, the force also doubles.
Explanation of how increasing the distance between two charges decreases the electrostatic force, using an analogy of a relationship's strength with proximity.
Application of Coulomb's Law to calculate the change in force when the distance between charges is doubled and the magnitude of the charges remains the same.
Demonstration of how the force between charges changes when the distance is altered, using a practical example of a positive and a negative charge separated by a certain distance and the force acting on each charge.
Use of Coulomb's Law to explain the significant increase in force when the distance between charges is reduced and the magnitude of the charges is increased.
Introduction to a simple math problem to calculate the magnitude of the force between two charges using Coulomb's Law, with given values for charge magnitudes and separation distance.
Explanation of what electric charge represents, with a positive charge indicating more protons than electrons and a negative charge indicating more electrons than protons.
Calculation of the number of excess protons representing a given charge, using the charge of a single proton as a conversion factor.
Determination of the net electric charge of an object with a given number of electrons and protons, using the formula q = (number of protons - number of electrons) * charge of a proton/electron.
Discussion on the direction of the net electric force acting on a charge situated between multiple charges of the same magnitude and equally spaced apart.
Introduction to the concept of electric fields, defined as the force exerted on a positive test charge divided by the magnitude of that test charge.
Explanation of how the electric field is represented by a vector and how it can be added graphically to determine the resultant force on a charge.
Illustration of how a positive charge will experience a force in the same direction as the electric field, while a negative charge will experience a force in the opposite direction.
Application of the concept of electric fields to determine the direction of the net electric field at various points in the presence of multiple charges.
Discussion on the work done by an electric field on a charge, differentiating between positive and negative work based on the direction of force and displacement.
Introduction to electric potential, defined as the ratio of electric potential energy to charge, with the unit being the volt.
Explanation of how electric potential energy is related to the work done on a charge as it moves through an electric field or potential difference.
Conclusion on the importance of understanding the difference between electric potential, voltage, and electric potential energy, and how they relate to the work done on or by a charge in an electric field.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: