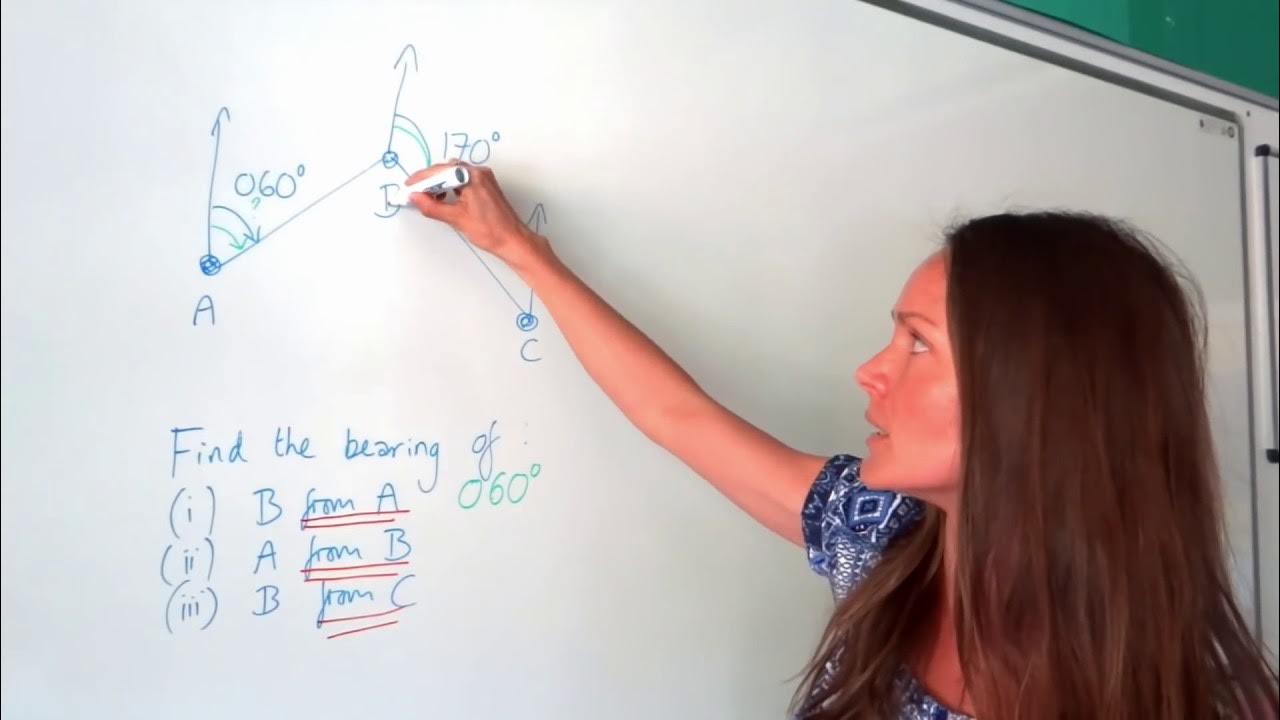
Bearings || Exam question ||
TLDRIn this informative YouTube video by ASI Chamber Jacob, viewers are introduced to the concept of bearings, a topic within the realm of navigation and geometry. The presenter, Jacob, explains the importance of understanding the North line and how to calculate the bearing between two points, C and D. He uses the properties of triangles and circles, such as the sum of angles in a triangle equaling 180 degrees and the total degrees in a circle being 360 degrees, to guide viewers through solving for bearings. The video provides a step-by-step approach to finding the bearing from point A to B and from B to O, using the properties of isosceles triangles and straight lines. Jacob emphasizes the significance of these geometric properties in determining the correct bearing angles. The video concludes with a reminder to subscribe to the channel and offers online tuition services in subjects like mathematics, English, civic education, biology, and science.
Takeaways
- 📍 To find the bearing between two points, you need to understand the concept of North and the method of drawing lines between points.
- 📐 The North line is a reference line pointing upwards at 90 degrees, which is used as a starting point for determining bearings.
- 🔍 When calculating bearings, you move from the starting point until you touch the line connecting the two points to find the angle of the bearing.
- 🔢 The angles around a point add up to 360 degrees, which is a key property when dealing with bearings and navigation.
- 🧩 The property of a triangle states that the sum of the interior angles equals 180 degrees, which is useful for solving bearing problems.
- ↗️ For bearings, if you have two points, the angle from one point to the North is equal to the angle from the North to the other point.
- 📐 In an isosceles triangle, where two sides are equal, the angles opposite those sides are also equal, which helps in calculating bearings.
- 🔢 To find the bearing from one point to another, you can use the property of a straight line, which is 180 degrees.
- 🔄 When calculating bearings, you can use the property of a circle, where the total angle around a circle is 360 degrees, to find the remaining angle.
- 📝 For complex bearing problems, you can use a combination of the properties of triangles, straight lines, and circles to find the solution.
- 📱 The speaker offers online tuitions in various subjects, including mathematics, English, civic education, biology, science, and additional mathematics.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the concept of bearings in geometry, specifically how to calculate and interpret them.
What is the first property mentioned for understanding bearings?
-The first property mentioned is the understanding of the North direction, which is the line pointing upwards at 90 degrees.
How do you find the bearing of point C from point D?
-To find the bearing of point C from point D, you start from point C, align with the North direction, and then draw a line to point D. The angle formed when you align with North and touch the line CD is the bearing.
What is the significance of the property that all angles inside a triangle add up to 180 degrees?
-This property is significant because it helps in calculating the unknown angles within a triangle when the other angles or side lengths are known.
What is the total angle measure of a circle according to the video?
-According to the video, the total angle measure of a circle is 360 degrees.
How does the property of an isosceles triangle help in finding the angles?
-In an isosceles triangle, where two sides are equal, the angles opposite those sides are also equal. This property helps in finding the measure of the angles when one of them is known.
What is the process to find the bearing of point B from point A?
-To find the bearing of point B from point A, you start from point A, establish the North line, and then move in the direction of the North line until it intersects with the line joining points A and B. The angle formed at point A is the bearing.
How is the property of a straight line used in the calculation?
-The property of a straight line, which states that the sum of angles around a point on a straight line is 180 degrees, is used to find the measure of unknown angles when other angles in the same line are known.
What is the final answer for the bearing of point O from point B?
-The final answer for the bearing of point O from point B is 280 degrees.
What services does ASI Chamber Jacob offer?
-ASI Chamber Jacob offers online tuitions in subjects such as mathematics, English, civic education, biology, science, and additional mathematics.
How can one get in touch with ASI Chamber Jacob for online tuitions?
-One can get in touch with ASI Chamber Jacob for online tuitions by calling or Whatsapping the number provided, which is 260969-175701.
What is the importance of understanding the properties of bearings, triangles, and circles in the context of the video?
-Understanding the properties of bearings, triangles, and circles is crucial for solving geometrical problems related to directions and angles, which is the core focus of the video's educational content.
Outlines
📚 Introduction to Bearings and Basic Properties
The first paragraph introduces the topic of bearings and outlines the fundamental properties necessary to understand bearings. The speaker explains that when calculating bearings, one must know the North direction, which is represented by a line pointing upwards at 90 degrees. The concept of finding the bearing from one point to another is introduced, using a visual method where a line is drawn from the starting point to the destination point, and the angle this line makes with the North line is the bearing. The importance of understanding angles and their relationships in a triangle and circle is emphasized, as these properties are crucial for solving bearing problems. The speaker also demonstrates how to calculate the bearing of point C from point D using the given angles and properties of a straight line and a triangle.
🔍 Calculating the Bearing of B from A Using Triangle Properties
In the second paragraph, the speaker delves into calculating the bearing of point B from point A using the properties of an isosceles triangle. The speaker identifies that two sides of the triangle are equal, which allows for the determination of the angles within the triangle. By subtracting one known angle from the total degrees in a triangle (180 degrees), the remaining angle is found and then divided by two to find the equal angles at the base of the triangle. The speaker uses the property that angles at the same position in respect to the North line are equal to establish the bearing angle. After calculating the angles, the speaker applies the property of a straight line to find the final bearing angle, which is determined to be 140 degrees.
🧮 Finding the Bearing of O from B Using Circle and Straight Line Properties
The third paragraph focuses on finding the bearing of point O from point B. The speaker begins by establishing the North line and then moves to find the angle between the points O and B. Using the property that corresponding angles are equal when a line is parallel to one side of a triangle, the speaker calculates the angle between the North line and the line joining O and B. By adding the known angles and subtracting from the total degrees in a circle (360 degrees), the speaker finds the final bearing angle. Two methods are demonstrated: one using the circle's property and another using the straight line's property, both leading to the same solution of 280 degrees. The speaker concludes with a reminder to subscribe to the YouTube channel and contact information for online tuitions in various subjects.
Mindmap
Keywords
💡Bearing
💡North
💡Tuition Center
💡Online Tuitions
💡Isosceles Triangle
💡Angle
💡Straight Line
💡Circle
💡Property
💡Calculation
💡Subscription
Highlights
The video discusses the concept of bearings in navigation and how to calculate them.
Understanding the properties of points, lines, and angles is key to solving bearing problems.
The North line, pointing upwards at 90 degrees, is a fundamental reference in bearing calculations.
To find the bearing from one point to another, align with the North line and draw a line connecting the two points.
The angle between the North line and the line connecting the two points gives the bearing.
Corresponding angles are equal when formed by parallel lines cut by a transversal.
The sum of angles around a point is 360 degrees, a key property used in solving bearing problems.
The video demonstrates how to find the bearing of point C from point D using the North line and angle properties.
The property that the sum of angles in a triangle is 180 degrees is used to find unknown angles.
In an isosceles triangle, the angles opposite the equal sides are themselves equal.
The video shows how to find the bearing of point B from point A using the properties of triangles and straight lines.
Subtracting known angles from 180 degrees allows finding the remaining unknown angle in a triangle.
The bearing of point O from point B is calculated using the North line, corresponding angles, and circle properties.
The solution for the bearing of O from B is obtained as 280 degrees using the circle and straight line properties.
The video provides a step-by-step approach to solving bearing problems using geometric properties.
Practicing finding bearings using different methods helps solidify understanding of geometric concepts.
The presenter offers online tuition in mathematics, English, civic education, biology, science, and additional mathematics.
Contact information is provided for those interested in online tuition with the presenter.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: