Bearings Exam questions
TLDRThe video script outlines a series of examples demonstrating how to calculate bearings in a geometric context. It begins with finding the bearing of point A from B using the property of a straight line and identifying angles. The second example involves calculating the bearing of point K from G, leveraging the properties of a circle and its angles. The third example focuses on the bearing of B from C, using the properties of a triangle to find the required angles. The presenter emphasizes the importance of understanding geometric properties and provides a step-by-step approach to solving each problem. The video concludes with an invitation to follow the channel for more educational content and an offer for online tuitions in various subjects, including mathematics, English, and science.
Takeaways
- 📐 **Bearing Calculation**: The script explains how to find the bearing from one point to another using properties of straight lines and angles.
- 🧭 **Starting Point**: The bearing calculation always starts from a designated point (e.g., B or G) and moves towards the north.
- 📏 **Property of Straight Lines**: Property number three is used to establish that a straight line extends 180 degrees from any point.
- 🔄 **Parallel Lines**: Property number one is applied to find angles when dealing with parallel lines, where corresponding angles are equal.
- 🔢 **Sum of Angles**: In a triangle, the sum of the interior angles is always 180 degrees (property number two), which helps in finding unknown angles.
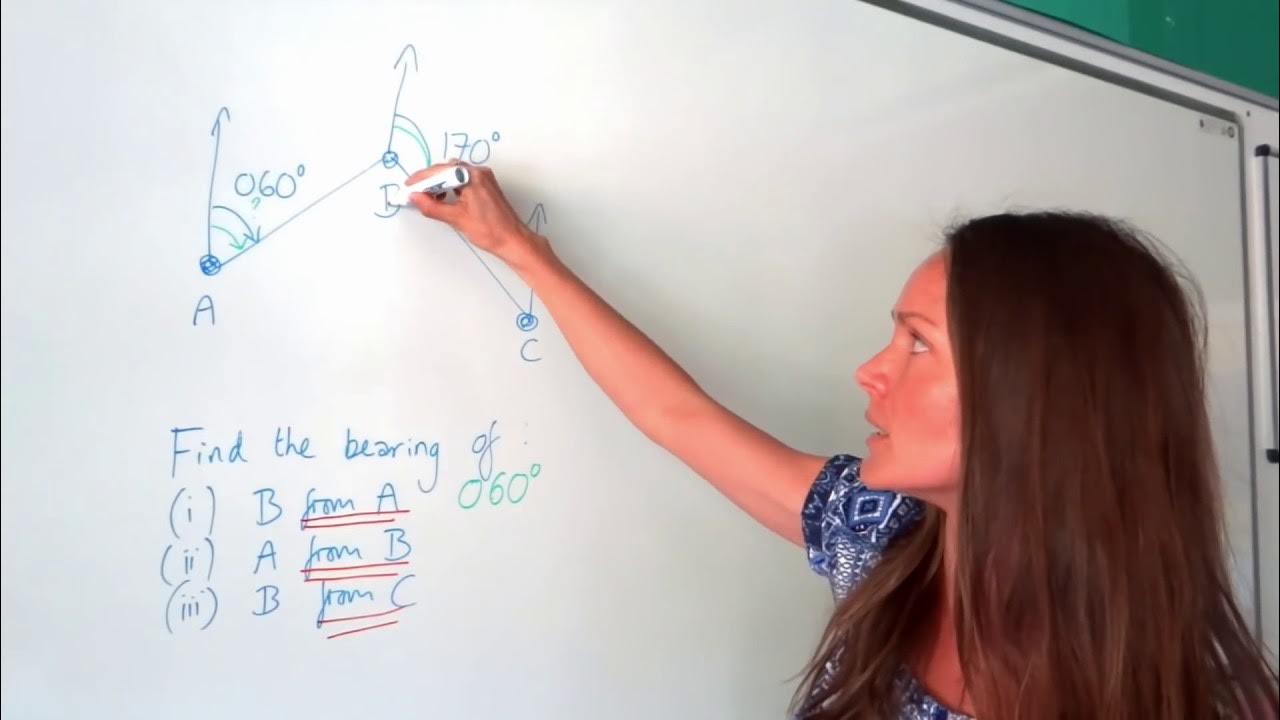
- 📐 **Bearing from B to A**: For example one, the bearing from B to A is found by using the given bearing and properties of lines and angles, resulting in a 250-degree angle.
- 📐 **Bearing from G to K**: In example two, the bearing from G to K is calculated by using the circle's property of 360 degrees and subtracting the given angle, resulting in a 300-degree angle.
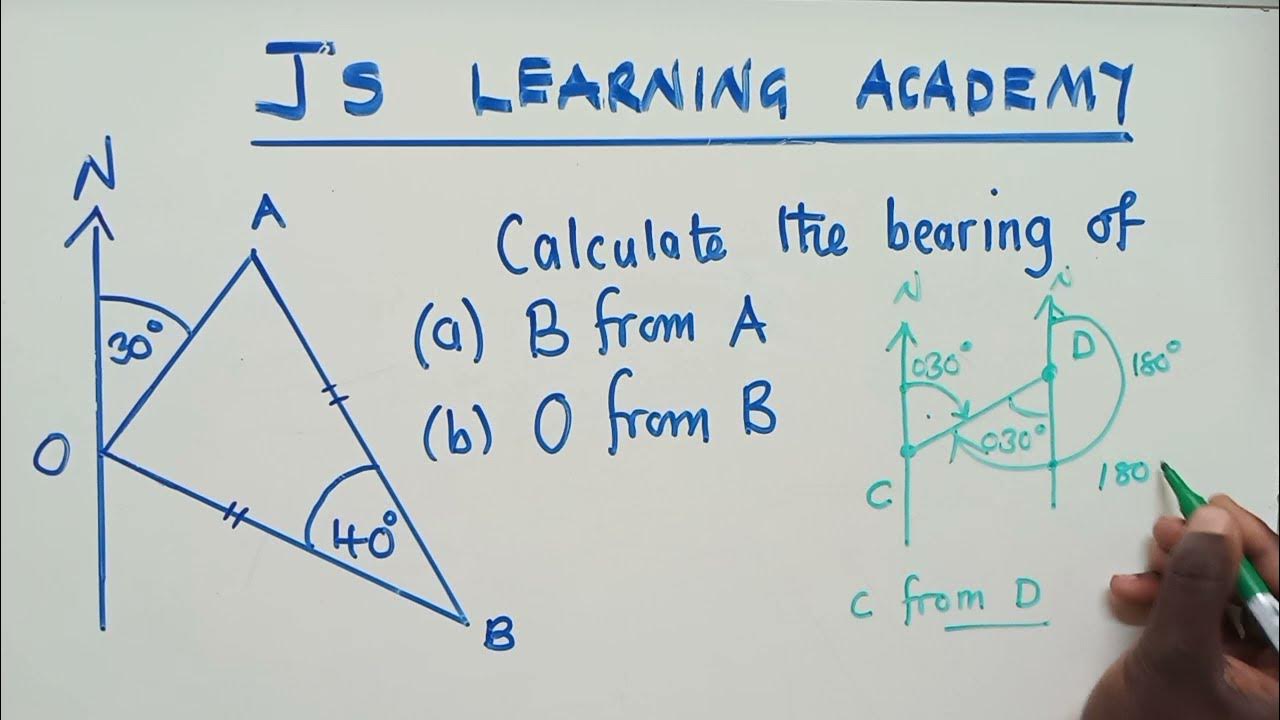
- 📐 **Bearing from C to B**: For the third example, the bearing from C to B is determined by subtracting the sum of two given angles from 180 degrees, leading to a 30-degree bearing.
- 🔴 **Use of Given Information**: The script emphasizes the importance of using the given angles and properties to calculate the unknown bearings.
- 📚 **Online Tuition Offer**: The speaker offers online tuition in various subjects including mathematics, English, biology, science, civic education, and commerce.
- 📞 **Contact Information**: Interested individuals can reach out for online classes via WhatsApp using the provided phone number.
- 🌐 **Social Media Presence**: The script mentions the availability of more educational content on YouTube and Tick Tock under the name 'Jacobusi Chamber'.
Q & A
What is the main topic of the provided transcript?
-The main topic of the transcript is finding the bearing from one point to another using geometric properties and angles.
What is the first property of a straight line mentioned in the transcript?
-The first property mentioned is that a straight line extends infinitely in both directions.
How is the bearing of A from B calculated in the transcript?
-The bearing of A from B is calculated by using the given bearing of 70 degrees, adding 180 degrees to it, and then using the property of parallel lines to find the total angle of 250 degrees.
What property of a circle is used in example number two to find the bearing of K from G?
-The property that the angle of a circle is 360 degrees is used to find the bearing of K from G.
What is the final bearing calculated for the bearing of K from G in example number two?
-The final bearing calculated for the bearing of K from G is 300 degrees.
In example number three, which property of a triangle is used to find the bearing of B from C?
-Property number two of a triangle, which states that the sum of the angles in a triangle is 180 degrees, is used to find the bearing of B from C.
What is the final bearing calculated for the bearing of B from C in example number three?
-The final bearing calculated for the bearing of B from C is 30 degrees.
What is the significance of the angle given as 70 degrees in the first example?
-The angle given as 70 degrees is significant because it is used as a reference to find the opposite angle, which is also 70 degrees, using the property of parallel lines.
How does the instructor suggest to find the angle when the bearing is already given?
-The instructor suggests using the given bearing and geometric properties such as the straight line property and the property of parallel lines to find the required angle.
What is the purpose of the online tuitions mentioned in the transcript?
-The purpose of the online tuitions is to provide educational support in subjects like mathematics, English, biology, science, civic education, principles of accounts, and commerce.
How can one get in touch for online tuitions as mentioned in the transcript?
-To get in touch for online tuitions, one can WhatsApp the provided number (+26 096917507 or 01) for more information on how to join the online classes.
Where can one find more of the instructor's works or follow them for updates?
-One can find more of the instructor's works on YouTube and Tick Tock by searching for the name 'Jacobusi Chamber'.
Outlines
📐 Geometry Lesson: Finding Bearings
This paragraph introduces a geometry lesson focused on calculating bearings. The speaker explains how to find the bearing of point A from B using the properties of straight lines and angles. They utilize the given bearing of 70 degrees and apply geometric properties to find the angle between the lines. The process involves adding 180 degrees to the straight line angle and using the property of parallel lines to deduce the bearing. The final bearing calculated is 250 degrees.
🔍 Example Two: Bearing of K from G
The second paragraph moves on to another example, illustrating how to find the bearing of point K from G. The speaker uses the concept of a circle's 360-degree angle to subtract from the given angle of 60 degrees, resulting in a bearing of 300 degrees. This example demonstrates the application of geometric properties in a different context, emphasizing the circle's properties.
📐 Triangle Property: Bearing of B from C
The final paragraph discusses a third example, focusing on finding the bearing of point B from C. The speaker emphasizes the importance of identifying the north direction and using the property of a triangle where the sum of the angles equals 180 degrees. By subtracting the sum of two known angles from 180 degrees, they find the remaining angle. The process involves calculating the difference between the angles and applying the property of parallel lines to find the final bearing, which is determined to be 30 degrees.
📞 Online Tuition and Contact Information
The last paragraph provides information about online tuition services offered by the speaker. They cover a range of subjects including mathematics, English, biology, science, civic education, principles of accounts, and commerce. Interested individuals are encouraged to follow the speaker on social media platforms like YouTube and Tick Tock for more content. The speaker also provides a contact number for those interested in joining online classes.
Mindmap
Keywords
💡Bearing
💡Straight Line
💡Property of a Triangle
💡Parallel Lines
💡Circle
💡Angles
💡North
💡Sum of Angles
💡Prolong
💡Online Tuitions
Highlights
Lesson 1 discusses finding the bearing of point A from point B using the property of a straight line.
Property number 3 states that a straight line measures 1980 degrees when prolonged.
To find the bearing, add 180 degrees to the given angle of 70 degrees.
Property number 1 is used to extend lines and establish parallel lines.
Angles on a straight line are equal, so if one angle is 70 degrees, the opposite angle is also 70 degrees.
Adding 100, 80 and 70 degrees gives a total of 250 degrees for the bearing.
In example 2, the bearing of point K from point G is found using property number 4.
The angle of a circle is 360 degrees, so subtracting 60 degrees leaves 300 degrees for the bearing.
Example 3 involves finding the bearing of point B from point C using the property of a triangle.
The sum of angles in a triangle is 180 degrees, so subtract the sum of the other two angles from 180 to find the bearing.
Subtracting 40 degrees from 70 degrees gives a bearing of 30 degrees.
The video provides step-by-step instructions on using geometric properties to find bearings.
The presenter uses visual aids to clearly demonstrate the process.
The video covers three examples to illustrate the concepts.
The presenter emphasizes the importance of understanding geometric properties to solve bearing problems.
The video concludes with information about online tuitions in various subjects offered by the presenter.
The presenter provides a contact number for interested students to inquire about online classes.
The video is part of a series on online math education available on YouTube and TikTok.
The presenter encourages viewers to follow, like and share the video for more educational content.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: