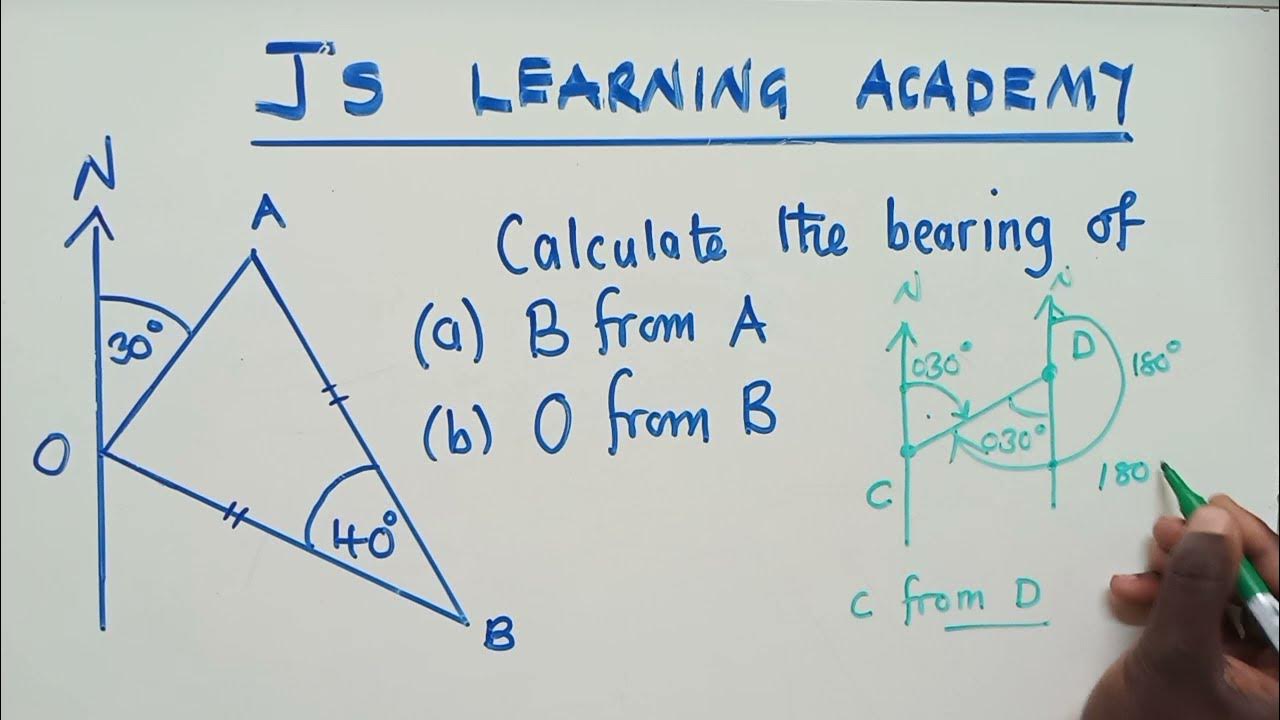
How To: Bearings Problem - VividMath.com
TLDRThe video script discusses the concept of finding the bearing from point A to point O, using the phrase 'you can't unscramble an egg' as a metaphor for the impossibility of reversing certain actions. However, the speaker challenges this notion by illustrating how one can indeed find the reverse bearing with the right approach. The video begins by drawing a diagram with north, south, east, and west marked to establish a reference point. Given a bearing from A to O of 130 degrees, the task is to find the reverse bearing. The speaker emphasizes the importance of starting with north and using geometry to determine the angles involved. By identifying corresponding angles formed by parallel lines, the video explains how to calculate the angle at the red dot, which is crucial for determining the reverse bearing. After calculating the angle to be 50 degrees, the final step is to subtract this from the full revolution of 360 degrees, resulting in a bearing of 310 degrees from O to A. The video concludes with a call to action to visit the website for additional resources and to subscribe for access to answers and offers.
Takeaways
- 🔍 The phrase 'you can’t unscramble an egg' is used metaphorically to discuss the concept of not being able to go backwards, which is the central theme of the problem-solving approach in the transcript.
- 📐 The problem involves finding the bearing of point O from point A, which means determining the direction from A to O.
- ➡️ Given the bearing from A to O is 130 degrees, the task is to find the reverse bearing from O to A.
- 🧭 Bearings are measured clockwise from North, and it's crucial to start with North when calculating bearings.
- 📈 A well-drawn diagram is essential for solving the problem, emphasizing the importance of visual representation in understanding and solving mathematical problems.
- 📏 The use of a ruler to draw crosses for North, East, South, and West on the diagram helps to establish a clear reference for the bearing calculation.
- 🔢 The angle between the bearing line and a parallel line is identified as a key to finding the reverse bearing, highlighting the role of geometry in bearing problems.
- 🤔 The concept of alternate angles is introduced as a method to find the unknown angle in the diagram, which is necessary for calculating the reverse bearing.
- 📐 By knowing that straight lines form angles of 180 degrees, the script guides through a process of subtraction to find the alternate angle.
- 🕵️♂️ The angle at the red dot is determined to be 50 degrees using the properties of alternate angles and the given bearing.
- 🔄 The final bearing from O to A is found by subtracting the identified angle (50 degrees) from the full revolution (360 degrees), resulting in a bearing of 310 degrees.
- 📚 The transcript encourages viewers to visit the website for additional resources, emphasizing the availability of further learning materials beyond the video content.
- 📧 Lastly, the transcript reminds viewers to subscribe for access to ready answers and special offers, indicating the value of ongoing engagement with the educational platform.
Q & A
What is the phrase 'You can’t unscramble an egg' often used to illustrate?
-The phrase is often used to illustrate the concept of irreversibility, meaning that certain actions or processes cannot be undone.
What is the task given in the transcript?
-The task is to find the bearing of point O from point A, which involves determining the direction from A to O.
What is the bearing given from point A to point O?
-The bearing from point A to point O is given as 130 degrees.
Why is it important to draw a diagram when solving bearing problems?
-Drawing a diagram is important because it helps visualize the problem, making it easier to understand the spatial relationships and solve the problem.
What does the speaker suggest drawing on the diagram?
-The speaker suggests drawing a cross to represent the cardinal directions: north, east, south, and west.
What is the significance of the angle marked with a dot in the transcript?
-The angle marked with a dot is significant because it is used to calculate the unknown bearing by subtracting it from the total angle of revolution (360 degrees).
What is the total angle of revolution mentioned in the transcript?
-The total angle of revolution is 360 degrees.
How can geometry be used to solve bearing problems?
-Geometry can be used to solve bearing problems by identifying and calculating angles formed by parallel lines, such as corresponding angles, alternate angles, and co-interior angles.
What property of parallel lines is used to find the equal angles in the bearing problem?
-The property of alternate angles is used to find the equal angles in the bearing problem, as they are equal when two lines are parallel.
What is the final calculated bearing of point O from point A?
-The final calculated bearing of point O from point A is 310 degrees.
What additional resources are mentioned in the transcript for further learning?
-The transcript mentions a website, http://www.vividmaths.com, which offers additional resources, cheat sheets, transcripts, and other math videos not available on YouTube.
What is encouraged for those interested in getting access to ready answers for math questions?
-The speaker encourages the audience to subscribe to gain access to all the ready answers for their math questions, as well as other special offers.
Outlines
📐 Understanding Bearings and Geometry
This paragraph introduces the concept of bearings in navigation, using the phrase 'you can't unscramble an egg' as an analogy to explain that while one cannot physically reverse an action like scrambling an egg, one can figuratively reverse directions in terms of bearings. The focus is on finding the bearing of point O from point A, given that the bearing from A to O is 130 degrees. The explanation involves drawing a diagram with north, south, east, and west, emphasizing the importance of starting with north when calculating bearings. It also touches on the use of geometry to solve the problem, specifically mentioning the application of alternate angles when dealing with parallel lines. The key step is to identify an angle that, when subtracted from the total 360-degree revolution, will yield the desired bearing. The process involves finding an angle formed by the intersection of the bearing line and the north-south axis, using the fact that the sum of angles around a point is 360 degrees and that alternate angles are equal.
🧮 Calculating the Reverse Bearing
The second paragraph continues the explanation of calculating the reverse bearing from point A to point O. It begins by identifying the angle that needs to be calculated, which is marked with a dot on the diagram. The process involves understanding that the total angle around a point is 360 degrees and that by subtracting the given bearing (130 degrees) from 180 degrees (the angle formed by a straight line), one can find the angle in question. This angle is found to be 50 degrees. The paragraph then explains that due to the parallel nature of the north-south lines, the alternate angles formed are equal, which means the angle in question is also 50 degrees on the opposite side. Finally, the bearing from O to A is calculated by subtracting this angle from the full revolution of 360 degrees, resulting in a bearing of 310 degrees. The paragraph concludes with a call to action to visit the website for additional resources and to subscribe for access to answers and special offers.
Mindmap
Keywords
💡Unscramble an egg
💡Bearing
💡North, East, South, West
💡Diagram
💡Clockwise
💡Geometry
💡Parallel Lines
💡Alternate Angles
💡Supplementary Angles
💡Revolution
💡VividMaths
Highlights
The phrase 'you can't unscramble an egg' is used to introduce the concept of going backwards in a problem, specifically finding the bearing of point O from point A.
The given information is the bearing from A to O, which is 130 degrees. The task is to find the bearing from O to A by going backwards.
Drawing a diagram is crucial, as a well-drawn problem is half-solved. A cross is drawn at point A to represent north, east, south, and west.
Bearings are important as they start at north and are measured clockwise. The bearing of 130 degrees from A to O is drawn on the diagram.
To find the bearing from O to A, the angle between the north-south line and the line from O to A needs to be determined.
Geometry concepts like corresponding angles, alternate angles, and parallel lines can be applied to solve the problem.
The angle between the north-south line and the line from O to A is marked with a dot on the diagram.
The angle of revolution, which is 360 degrees, is subtracted by the given bearing of 130 degrees to find the angle at the red dot.
The angle at the red dot is calculated to be 50 degrees using the formula 180 - 130 = 50.
Since the lines are parallel, the alternate angles are equal, so the angle at the red dot is also 50 degrees on the other side.
The final step is to subtract the angle at the red dot (50 degrees) from the angle of revolution (360 degrees) to find the bearing from O to A.
The bearing from O to A is calculated to be 310 degrees by subtracting 50 from 360.
The bearing of 310 degrees represents the direction from O to A in a clockwise direction from north.
The website http://www.vividmaths.com offers additional resources, cheat sheets, transcripts, and math videos not available on YouTube.
Subscribing to the website provides access to ready answers for math questions and other special offers.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: