Maths Help: Finding Bearings - VividMath.com
TLDRThe video script introduces a fundamental concept in bearings, emphasizing the importance of always starting from the north and moving clockwise. It demonstrates how to calculate bearings using three different angles: 30 degrees from the east, 180 degrees plus 19 degrees from the south, and 360 degrees minus 32 degrees from the north. The first bearing from O to A is calculated as 60 degrees, the second from O to B as 199 degrees, and the third from O to C as 328 degrees. The video also encourages viewers to visit the website www.vividmaths.com for additional resources and to subscribe for access to answers to all math questions and special offers.
Takeaways
- 🧭 Always begin with North: The concept of bearings always starts from the North and proceeds clockwise.
- 🔢 Calculate the first bearing: Subtract the given angle from 90 degrees to find the bearing from North to the first point (A).
- 🔄 Understand supplementary angles: When moving from North to South, you cover 180 degrees, which is a straight line.
- 📏 Add the remaining angle: To find the second bearing (B), add the specific angle to 180 degrees.
- 🔁 Complete the circle: For the third bearing (C), start from North and move 360 degrees minus the given angle.
- 🤔 Recognize complementary angles: The bearing from North to the first point is found by subtracting the given angle from 90 degrees, which are complementary.
- 📐 Use a calculator: When adding or subtracting angles, especially for larger bearings, use a calculator for precision.
- 📈 Sequential process: Calculate each bearing step by step, ensuring accuracy in each step before moving to the next.
- 🌐 Visit the website for more resources: For additional learning materials, visit http://www.vividmaths.com.
- 📚 Access additional content: The website offers resources, cheat sheets, transcripts, and exclusive video content not available on YouTube.
- 🔔 Subscribe for updates: Don't forget to subscribe to the channel for access to answers to all math questions and special offers.
Q & A
What is the primary concept for determining bearings as described in the transcript?
-The primary concept for determining bearings is to always begin at north and proceed in a clockwise direction.
What direction is considered as the starting point for bearing calculations?
-North is considered as the starting point for bearing calculations.
If a random angle is 30 degrees from the east, what is the bearing from north to that point?
-The bearing from north to a point 30 degrees from the east is 60 degrees, calculated by subtracting 30 degrees from 90 degrees.
What is the bearing from north if you go straight down to the south?
-The bearing from north to the south is 180 degrees, as it forms a straight line supplementary to the north.
How do you calculate the bearing from north to a point that is 19 degrees sweeping across from the south?
-You calculate it by adding the 19 degrees to the 180 degrees from north to south, resulting in a bearing of 199 degrees.
What is the bearing from north if you go all the way around, which is 360 degrees, and then subtract 32 degrees?
-The bearing from north after a full revolution of 360 degrees and then subtracting 32 degrees is 328 degrees.
What is the significance of always starting with north in bearing calculations?
-Starting with north establishes a consistent reference point, which is essential for accurately determining bearings in a clockwise direction.
How does the concept of complementary angles apply in finding bearings?
-Complementary angles are used to find the remaining angle needed to reach a specific bearing from north by subtracting the known angle from 90 degrees.
What additional resources can be found on the website mentioned in the transcript?
-The website http://www.vividmaths.com offers additional resources, cheat sheets, transcripts, and other math videos not available on YouTube.
What is the importance of subscribing on the website for access to math answers and special offers?
-Subscribing provides access to ready answers for all math questions and other exclusive offers, enhancing the learning experience and providing extra support.
Why is it necessary to understand the concept of a full revolution when calculating bearings?
-Understanding a full revolution (360 degrees) is necessary to correctly calculate bearings that involve going all the way around and then adjusting for a specific angle, as in the case of subtracting 32 degrees.
How can one ensure they are calculating bearings correctly?
-One can ensure they are calculating bearings correctly by always starting from north, proceeding in a clockwise direction, and using the principles of complementary and supplementary angles where applicable.
Outlines
🧭 Understanding Bearings: The North-Centric Approach
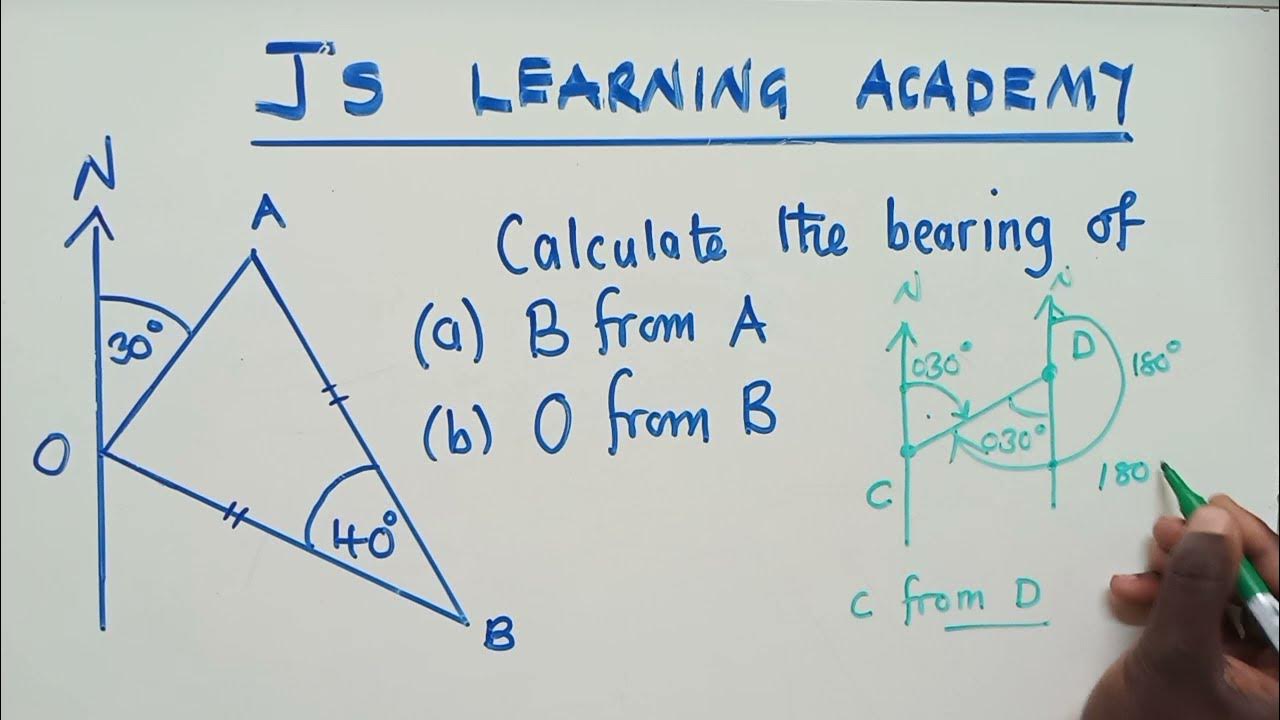
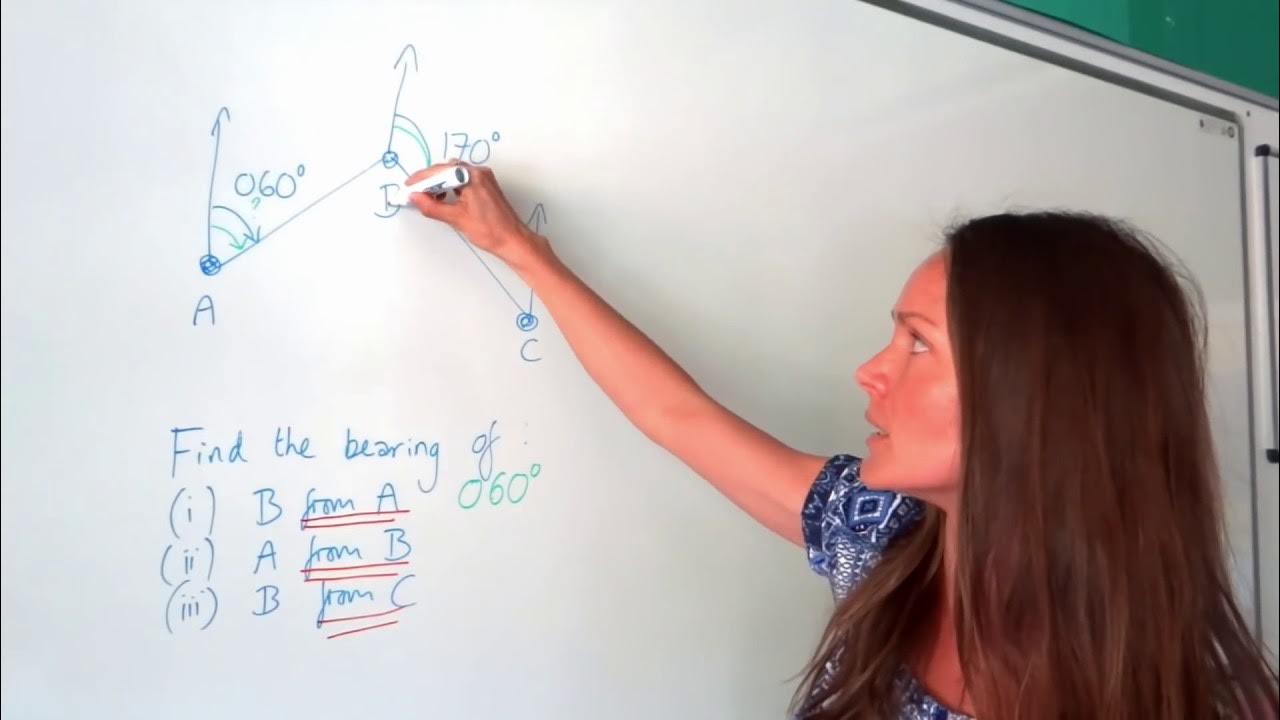
The first paragraph introduces the concept of bearings, emphasizing the importance of always starting from the north and moving clockwise. The speaker uses a diagram to illustrate different angles and how to convert them into bearings. The process involves calculating the bearing from a starting point 'O' to different points 'A', 'B', and 'C' by subtracting given angles from 90, 180, and 360 degrees respectively. The key takeaway is that bearings are determined by starting at north and sweeping clockwise, with the final bearings calculated as 60, 199, and 328 degrees.
📚 Additional Resources and Subscription Offer
The second paragraph is a call to action, directing viewers to visit the website http://www.vividmaths.com for additional resources such as cheat sheets, transcripts, and exclusive video content not available on YouTube. It also encourages viewers to subscribe to gain access to answers for all math questions and to receive other special offers.
Mindmap
Keywords
💡bearings
💡north
💡clockwise
💡random angle
💡complementary
💡supplementary
💡calculator
💡revolution
💡vividmaths.com
💡subscription
💡cardinal directions
💡degrees
Highlights
The concept of bearings is introduced, which is crucial for understanding navigation and direction.
Bearings always begin at north and proceed in a clockwise direction, which is a fundamental principle.
The first example involves finding the bearing from a random angle of 30 degrees from the east.
The second example shows how to calculate the bearing when there is a 180-degree line from north to south, adding an additional 19 degrees.
The third example demonstrates calculating the bearing when starting from north and moving almost a full 360-degree revolution, minus a 32-degree gap.
A key takeaway is that no bearing can happen without starting from north, emphasizing the importance of the north as a reference point.
The process of calculating bearings is made visual through diagrams, aiding in the understanding of the concept.
Complementary angles are used in the calculation of bearings, as shown in the first example where 90 degrees minus 30 degrees equals 60 degrees.
For the second bearing, the concept of supplementary angles is introduced, where 180 degrees plus an additional angle gives the total bearing.
The final bearing example involves a full 360-degree revolution minus a specific angle to find the clockwise bearing from north.
The transcript provides a step-by-step guide to calculating bearings, making the concept more accessible to learners.
The importance of understanding angles and their relationships is highlighted as a prerequisite for grasping the concept of bearings.
The use of a calculator is mentioned for adding angles together, showing the practical aspect of bearing calculations.
The transcript ends with a call to action, encouraging viewers to visit the website for additional resources and to subscribe for more math help.
VividMaths.com is promoted as a resource for further learning, including cheat sheets, transcripts, and videos not available on YouTube.
Subscription is positioned as a way to get access to answers for all math questions and other special offers.
The transcript is designed to comfort and assure learners that understanding bearings will lead to confidence in navigation and direction.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: