Sine & Cosine Rules applied to Bearings : ExamSolutions Maths Revision
TLDRThe video script presents a detailed explanation of solving a navigation problem involving bearings using trigonometric rules, specifically the Sine and Cosine rules. The scenario involves a ship traveling from point A to B on a bearing of 40 degrees for 3 kilometers, then altering course to point C on a bearing of 160 degrees for 5 kilometers. The challenge is to find the distance AC and the bearing of A from C. The solution process involves drawing a diagram, applying the Cosine rule to find AC, and then using the Sine rule to determine the angle theta, which is crucial for calculating the bearing from C to A. The presenter emphasizes the importance of extending lines for clarity and uses a step-by-step approach to guide viewers through the calculations, ultimately finding AC to be approximately 4.4 kilometers and the bearing from C to A to be 303 degrees.
Takeaways
- 📐 **Bearing Calculation**: The script discusses the calculation of bearings using trigonometric rules, specifically the sine and cosine rules.
- 🚢 **Ship's Journey**: The example involves a ship that sails from point A on a bearing of 040 degrees for 3 km to point B, then changes course to a bearing of 160 degrees for 5 km to point C.
- 🧭 **Bearing Definition**: Bearings are measured clockwise from the north direction, which is crucial for understanding the ship's direction changes.
- 📏 **North-South Line Extension**: Extending the north-south line is recommended for clarity when working with bearings, as it helps in using alternate angles and the concept of 180 degrees.
- 🔢 **Cosine Law Application**: The cosine law is used to find the distance AC by knowing two sides and the included angle (60 degrees) between them.
- 🔑 **Angle Calculation**: The angle θ is calculated using the sine rule, which relates the ratio of the length of a side of a triangle to the sine of the angle opposite that side.
- 🔍 **Trigonometric Functions**: The sine of 60 degrees and its relationship with the sides of the triangle are used to find angle θ.
- 📐 **Inverse Sine Function**: The inverse sine function is applied to find the measure of angle θ from its sine value.
- 🔢 **Bearing Calculation Method**: The bearing of A from C is determined by adding the known angles and subtracting from 360 degrees.
- 📐 **Significance of Extending Lines**: The script emphasizes the importance of extending lines from the north through the point to the south for better angle and bearing calculations.
- 📝 **Accuracy in Calculations**: The script advises to use unrounded values for trigonometric calculations to maintain precision, rounding only at the end for the final answer.
- 📊 **Use of Calculator**: A calculator in degree mode is essential for accurate trigonometric calculations and finding the inverse sine of a value.
Q & A
What is the initial bearing of the ship from point A?
-The initial bearing of the ship from point A is 040 degrees.
How far does the ship travel from point A to point B?
-The ship travels 3 kilometers from point A to point B.
What is the bearing of the ship from point B to point C?
-The bearing of the ship from point B to point C is 160 degrees.
How far does the ship travel from point B to point C?
-The ship travels 5 kilometers from point B to point C.
Why is it important to extend the North-South line when drawing the diagram?
-Extending the North-South line helps in using alternate angles and the concept of 180 degrees, which are crucial for solving the problem.
What trigonometric rule is used to find the distance AC?
-The cosine rule is used to find the distance AC.
What is the value of angle ABC?
-Angle ABC is 20 degrees, which is the remainder of 180 degrees minus 160 degrees.
How is the cosine rule applied to find AC?
-The cosine rule is applied by squaring side AC, and equating it to the sum of the squares of the other two sides (3 and 5), minus twice the product of those two sides multiplied by the cosine of the angle between them (60 degrees).
What is the approximate distance AC in kilometers?
-The approximate distance AC is 4.4 kilometers when rounded to two significant figures.
Which trigonometric rule is chosen to find angle theta?
-The sine rule is chosen to find angle theta.
What is the approximate value of angle theta in degrees?
-The approximate value of angle theta is 36.586 degrees.
How is the bearing of A from C calculated?
-The bearing of A from C is calculated by adding the 20 degrees to angle theta (36.586 degrees) and subtracting the sum from 360 degrees, then rounding to the nearest degree to get a bearing of 303 degrees.
Outlines
🚢 Working with Bearings: Sine and Cosine Rule Introduction
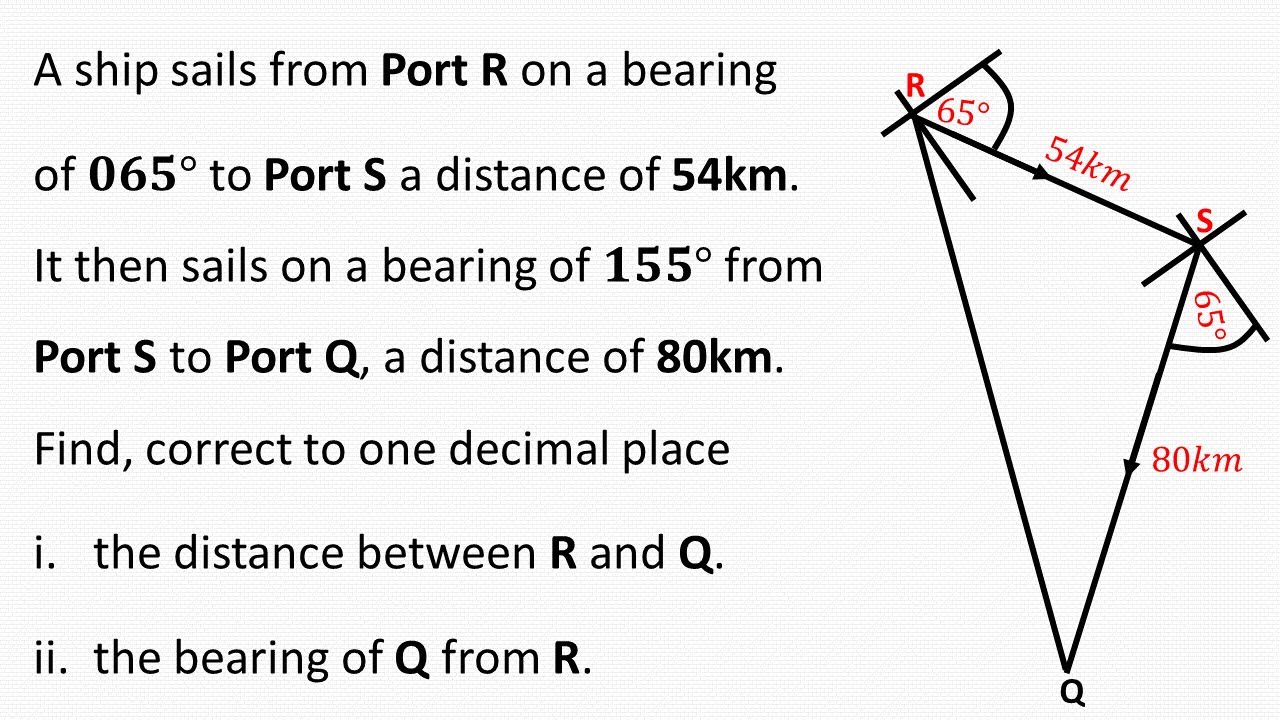
This paragraph introduces the problem of working with bearings using the sine and cosine rules. It begins with a scenario where a ship sails from point A on a bearing of 040 degrees for 3 kilometers to point B. The speaker advises on drawing a diagram, marking points, and extending lines for clarity. The ship then alters its course to a bearing of 160 degrees for 5 kilometers to reach point C. The challenge is to find the distance AC and the bearing of A from C. The cosine law is mentioned as a method to find the distance AC, given the two legs of the journey and the angle between them.
📐 Applying Cosine and Sine Rules to Find Distance and Bearing
The speaker provides a step-by-step guide to solving the problem. Using the cosine rule, the distance AC is calculated by squaring the unknown side, adding the squares of the other two known sides, and subtracting twice the product of those sides multiplied by the cosine of the angle between them. The angle is found to be 60 degrees, and after calculation, AC is found to be approximately 4.4 kilometers, rounded to two significant figures. To find the bearing of A from C, the speaker introduces an angle theta, which is required to determine the final bearing. Two methods are proposed: cosine rule and sine rule. The sine rule is chosen for its simplicity in this context, and the angle theta is calculated using the ratio of the sine of the angle to the opposite side. After finding theta, the bearing of A from C is determined by adding the known angle of 20 degrees to theta and subtracting from 360 degrees, resulting in a bearing of approximately 303 degrees.
📝 Conclusion and Encouragement
The final paragraph serves as a conclusion to the video script, offering encouragement to the viewer. It acknowledges that the problem might be challenging but commends those who were able to solve it correctly. The speaker expresses hope that the explanation provided is useful and offers assistance in case of any difficulties encountered by the viewer.
Mindmap
Keywords
💡Bearing
💡Sine Rule
💡Cosine Rule
💡North-South Line
💡Alternate Angles
💡Trigonometry
💡Calculator
💡Significant Figures
💡Diagram
💡Distance Calculation
💡Angle Calculation
Highlights
The transcript provides a step-by-step example of working with bearings using the sine rule and cosine rule.
The example involves a ship sailing from point A to B to C on specific bearings and distances.
Drawing a diagram is crucial for visualizing the problem and applying the rules effectively.
Extending lines from the north through the points to the south helps in using alternate angles and the 180-degree concept.
The ship sails 3 km from A to B on a bearing of 40 degrees, then 5 km from B to C on a bearing of 160 degrees.
To find the distance AC, the cosine law is used with the known sides of 3 km and 5 km and the angle between them.
The cosine law calculation results in AC being approximately 4.4 km when rounded to two significant figures.
Finding the bearing of A from C requires calculating the angle theta, which can be done using either the cosine rule or sine rule.
The sine rule is chosen to find theta by comparing the ratios of the sine of angle theta to side 3 and sine of 60 degrees to side AC.
Calculating theta using the sine rule results in an angle of approximately 36.59 degrees.
The bearing of A from C is found by subtracting theta from 360 degrees and adding 20 degrees, resulting in a bearing of approximately 303 degrees.
The transcript emphasizes the importance of extending lines and using alternate angles when working with bearings and trigonometric rules.
Using a north-south line is useful for visualizing angles and applying trigonometric concepts in bearings problems.
The sine and cosine rules are powerful tools for solving bearings problems involving unknown distances and angles.
The transcript provides a clear, step-by-step solution to the example problem, making it easy to follow along.
Practicing with different examples and applying the rules methodically can help in solving complex bearings problems.
The transcript assumes familiarity with the sine and cosine rules but encourages checking related videos for a deeper understanding.
Using a calculator in degree mode is important for accurate calculations of trigonometric functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: