Volume with Washers
TLDRThis video tutorial delves into the concept of calculating the volume of solids using the washer method, applicable to hollow or non-uniformly solid shapes. The presenter guides viewers through the process of finding volumes by rotating regions around different axes, using the area of annuli to determine the volume of 'washers' formed during rotation. The video covers multiple examples, illustrating the setup of integrals for volume calculation without necessarily evaluating them, and highlights various scenarios including rotation around non-horizontal axes, providing a comprehensive understanding of the washer method for volume calculation.
Takeaways
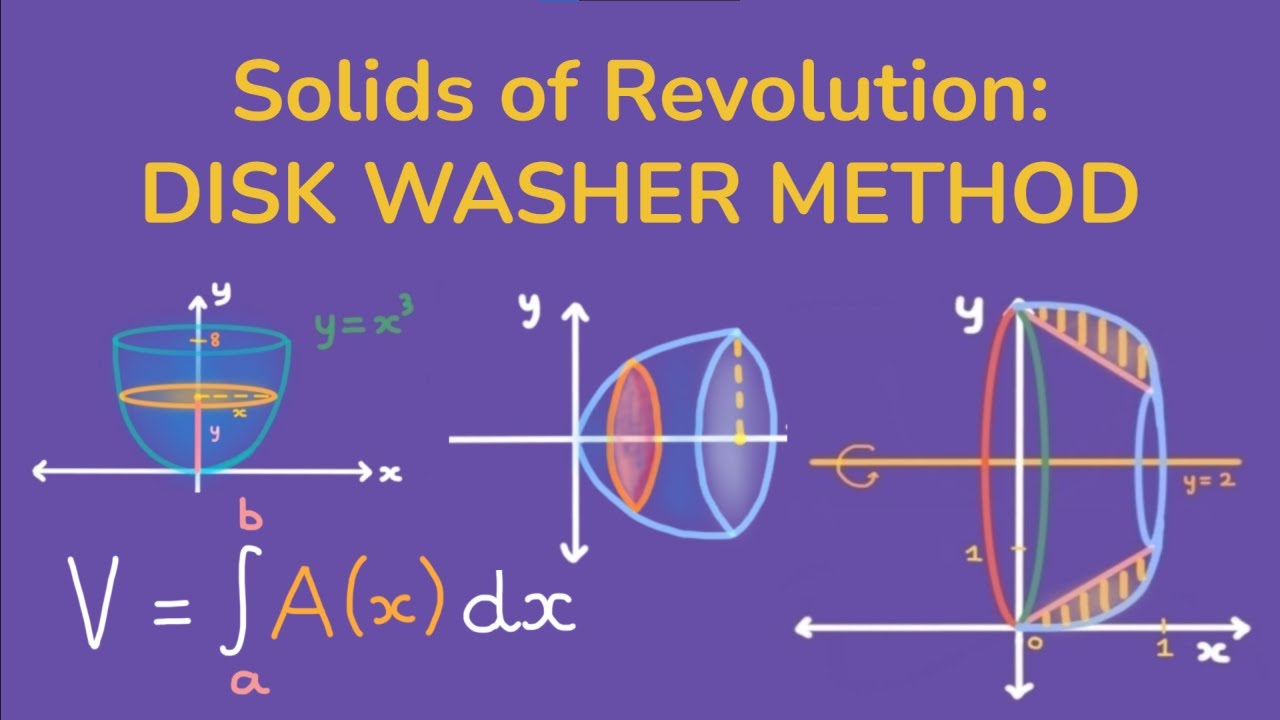
- 📚 The video discusses the concept of finding the volume of solids using the washer method, which involves rotating a region around an axis to create a hollow shape.
- 🔄 The first example involves rotating the region between y = x^2 and y = √x around the x-axis, resulting in a bowl-like shape with a convex interior.
- 📏 The area of an annulus, or washer, is calculated by subtracting the area of a smaller circle from a larger one, using the formula π(R^2 - r^2).
- 📐 The radii for the washer method are determined by the difference between the outer and inner functions of the region being rotated, considering 'top minus bottom' or 'right minus left'.
- ⭕ The intersection point of the functions y = x^2 and y = √x is at x = 1, which is important for understanding the limits of integration.
- 📊 The volume calculation involves summing the volumes of infinitesimally thin washers, which is represented by an integral of the form π∫(R^2 - r^2)dx.
- 🔢 The integration process simplifies to finding antiderivatives of the functions representing the difference in radii squared, and then evaluating between the limits of integration.
- 📉 The video also covers rotating regions around lines other than the x-axis, such as y = -2, which requires adjusting the radii calculations to account for the new axis of rotation.
- 📈 The volume of solids formed by rotating regions around vertical lines is found by integrating with respect to y, using the formula π∫(R^2 - r^2)dy.
- 🔧 The washer method is not always necessary; for rotation around certain axes, a disc method might be more appropriate, as demonstrated by the rotation around the line x = 2.
- 📝 The video emphasizes the importance of practice in both integration and algebra to master the technique of finding volumes using the washer method.
Q & A
What is the main topic of the video?
-The main topic of the video is integrating to find volume using the washer method for solids that are hollow or not completely solid throughout.
What is the first solid discussed in the video script?
-The first solid discussed is created by rotating the region between y = x^2 and y = √x around the x-axis, which resembles a bowl with a convex inside.
What is a washer in the context of this video?
-In this context, a washer refers to the cross-sectional shape formed when a region is rotated around an axis, which is an annulus or a ring shape with an area between two circles.
How is the area of an annulus calculated?
-The area of an annulus is calculated by taking the area of the larger circle (πR^2) and subtracting the area of the smaller circle (πr^2), where R and r are the radii of the larger and smaller circles, respectively.
What is the significance of the term 'top minus bottom' when determining the radii for the washer method?
-The term 'top minus bottom' is significant because it represents the distance from the axis of rotation to the edge of the solid being generated, which is crucial for determining the radii of the washer.
What is the intersection point of the functions y = x^2 and y = √x in the video script?
-The intersection point of the functions y = x^2 and y = √x is at x = 1, where both functions have the same y-value.
What is the strategy for setting up the integral to find the volume of a solid generated by rotating a region around an axis?
-The strategy involves setting up the integral of π times the difference of the squares of the large and small radii (R^2 - r^2) with respect to the variable of integration (usually x or y), over the range of the region.
How does rotating a region around a line other than the x-axis affect the calculation of the volume?
-Rotating a region around a line other than the x-axis requires considering the distance from the axis of rotation to the edge of the region (top minus bottom) for both the large and small radii, which may change the setup of the integral.
What is the difference between a washer method and a disc method for finding volume?
-The washer method involves finding the volume of a solid with a hollow center by subtracting the volume of a smaller solid from a larger one, while the disc method involves finding the volume of a solid without a hollow center by integrating the area of circular discs formed by rotating a region around an axis.
How does the video script illustrate the process of integrating to find volume using the washer method?
-The video script illustrates the process by providing step-by-step examples, including drawing the radii, setting up the integral with the washer formula, and explaining the significance of each step in the calculation.
Outlines
📚 Introduction to Volume Calculation Using Washers
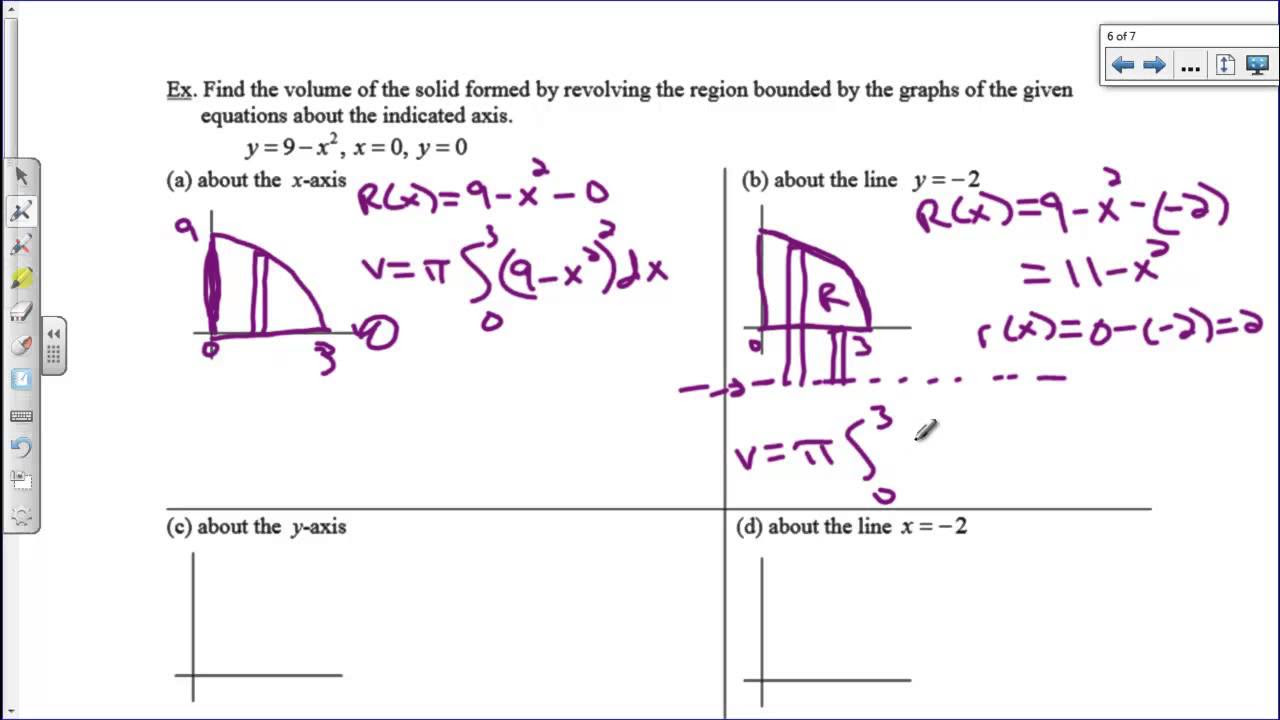
This paragraph introduces the concept of calculating the volume of solids with a hollow or non-uniform cross-section by using the washer method. The example involves rotating the region between the functions y=x^2 and y=√x around the x-axis to form a bowl-shaped solid. The process includes drawing representative rectangles and cross-sections, identifying the large and small radii for the washers, and setting up the integral to calculate the volume by subtracting the area of the smaller circle from the larger one, factoring out π, and integrating from 0 to 1 with respect to x.
🔄 Rotating Around Non-x Axis and Setting Up the Integral
The second paragraph discusses the process of rotating a region around the line y=-2, which is not the x-axis. The strategy involves identifying the large and small radii based on the axis of rotation and the region's edge. The volume calculation is set up using the integral of π times the difference of the squares of the large and small radii with respect to x, ranging from 1 to 6. The paragraph also mentions that typically on exams, the integral is set up but not evaluated, and it provides an example from the 2010 AB exam question 4.
🌋 Exploring Volumes with Complex Geometries and Axes
This paragraph explores the concept of rotating regions around different axes, such as y=7, and describes the resulting solid's geometry, like a cone with a hole. It discusses the process of setting up the integral for volume calculation with the large and small radii, considering the top and bottom functions, and the range of x from 0 to 9. The paragraph also touches on the strategy for integrating with respect to y and the importance of using the correct variable for integration.
📐 Advanced Techniques for Rotating Around Vertical Axes
The fourth paragraph delves into more complex scenarios of rotating regions around vertical axes, specifically x=5 and y-axis, and calculating the resulting volumes. It explains how to determine the large and small radii for these rotations, set up the integrals accordingly, and factor out π for the volume calculation. The paragraph also provides an example of rotating around the y-axis and simplifies the integral by considering only one radius, as there is no small radius in this case.
🔄 Final Thoughts on Washer Method and Disk Method
The final paragraph wraps up the discussion on the washer method by providing a brief overview of a disk problem, where the region is rotated around the line x=2, and only one radius is needed for the calculation. It emphasizes that not all volume problems require the washer method and that the disk method can be simpler in some cases. The paragraph concludes by summarizing the various cases covered in the video and encourages practice for better understanding and visualization of these concepts.
Mindmap
Keywords
💡Volume
💡Washers
💡Integration
💡Annulus
💡Cross Sections
💡Solids of Revolution
💡Radius
💡Disc Method
💡Axis of Rotation
💡Integration Limits
💡Power Rule
Highlights
Introduction to the concept of integrating to find volume using washers for hollow or partially solid objects.
Explanation of the first example involving rotation of the region between y=x^2 and y=√x around the x-axis to form a bowl-shaped solid.
Illustration of representative rectangles and washer cross-sections in the volume calculation process.
Formula for the area of an annulus, which is crucial for understanding the volume of solids formed by rotation.
Description of how to determine the large and small radii for the washer method, emphasizing the importance of 'top minus bottom'.
Integration setup for finding the volume of the solid formed by rotating the given region, factoring out constants for simplification.
Transition to a more complex example involving rotation around the line y=-2, requiring a different approach for radii calculation.
Clarification on how to handle the integration when the axis of rotation is not the x-axis, with an example involving rotation around y=-2.
Discussion on the significance of the intersection point x=1 in the context of the given functions.
Demonstration of setting up an integral for a volume problem without evaluating it, a common approach in exams.
Introduction of a 2010 AP exam question, highlighting the importance of setting up integrals for volume problems.
Explanation of how to adjust the washer method for solids that are below the axis of rotation, using a cone-shaped example.
Visual representation of the solid formed by rotation and its resemblance to a sideways volcano or an ice cream cone.
Calculation of the volume of a solid formed by rotating a region around the vertical line x=5, including the setup of the integral.
Conversion of the volume calculation to an integral with respect to y, showcasing the versatility of the washer method.
Final example demonstrating a disc problem, contrasting with the washer method and emphasizing the simplicity of the disc method.
Summary of the different cases for volume calculation using the washer technique, providing a comprehensive overview of the method.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: