Calculating volume by known cross sections
TLDRThe video script provides an in-depth exploration of calculating the volumes of solids formed by revolving known cross-sections around different axes. Mr. R explains the process of creating solids of revolution by revolving regions formed by the intersection of curves like y = x^2 and y = e^x around the x-axis, y-axis, or any arbitrary axis. The video introduces various methods, including using squares, semicircles, and equilateral triangles as cross-sections to build the solid. It covers the mathematical derivation for calculating the area of each cross-section and then integrating these areas to find the total volume. The script also uses GeoGebra to visually demonstrate the process and concludes with a reminder that any shape can theoretically be used for cross-sections, emphasizing the importance of understanding the area calculation and integration process for different shapes.
Takeaways
- 📐 **Cross-Sectional Volume Calculation**: The video discusses calculating the volume of solids formed by known cross-sections, such as squares, semicircles, and equilateral triangles, by integrating the area of these shapes along an axis.
- 🔄 **Solids of Revolution**: A common method to create a solid is by revolving a region formed by two curves around an axis, but the video introduces an alternative method of building solids by stacking shapes on top of cross-sections.
- 📈 **Graph Integration**: The process involves using the graph of functions like y = e^x and y = x^2 to determine the cross-sections and subsequently the volume of the solid formed by these sections.
- 🔢 **Integration for Volume**: The volume of the solid is found by integrating the area of the cross-sectional shapes (squares, semicircles, equilateral triangles) along the x-axis from specific bounds.
- 🟩 **Square Cross-Sections**: For squares perpendicular to the x-axis, the side length of the square is equal to the function value, and the area is the side length squared, which is integrated to find volume.
- 🟥 **Semicircle Cross-Sections**: When using semicircles, the radius is half the difference between two function values, and the area is calculated as (π/2) times the radius squared, then integrated.
- 🟫 **Equilateral Triangle Cross-Sections**: The base of an equilateral triangle is taken as the function value, and the area is derived using the formula (√3/4) times the base squared, which is then integrated.
- 📉 **Function Difference for Height**: The height or side length of the cross-sectional shape is determined by the difference in values of the two functions at each point along the axis of integration.
- 🧮 **Integration by Substitution**: The video demonstrates the use of substitution in integration, particularly when changing the bounds of integration after substituting a variable like U = 2x.
- 📋 **Memorising Formulas**: Memorising the area formulas for different shapes can speed up problem-solving, although the video also shows how to derive these formulas if they are not recalled.
- 📏 **Geometry and Calculus Connection**: The video highlights the connection between geometry (knowledge of triangle types and their properties) and calculus (integration) in solving these types of problems.
Q & A
What is the main topic of discussion in the provided transcript?
-The main topic of discussion is calculating volumes of solids formed by known cross-sections, specifically using different shapes like squares, semicircles, and equilateral triangles as cross-sectional areas to build up the volume through integration.
What is the first method described for creating a solid from a two-dimensional region?
-The first method described is revolving the region formed by two curves around an axis to create a solid of revolution.
How does the process of creating a solid by adding squares to each cross-section differ from revolving a region around an axis?
-Adding squares to each cross-section involves placing a square on top of each vertical slice of the region, with the side length of the square determined by the function's value at that point. This method builds the solid by stacking congruent squares along the axis, as opposed to revolving a region which creates a smooth solid by rotating the entire region around an axis.
What is the formula for the area of a square used as a cross-section?
-The area of a square is given by the square of its side length. In the context of the script, if the side length is determined by a function, say e^x, then the area of the square is e^(2x).
How is the volume of a solid created by stacking semicircles calculated?
-The volume is calculated by finding the area of each semicircle, which is π/2 times the square of the radius (the difference between the upper and lower function values), and then integrating this area along the x-axis within the bounds of the region.
What is the key formula used to calculate the area of an equilateral triangle?
-The key formula for the area of an equilateral triangle is (sqrt(3)/4) times the square of the side length, which is derived from the properties of a 30-60-90 right triangle formed by dropping an altitude from a vertex to the base of the equilateral triangle.
How does the shape of the solid formed by stacking equilateral triangles differ from the solid formed by stacking squares?
-The solid formed by stacking equilateral triangles has an angular, spiky appearance, resembling the back of a chameleon as described in the script. In contrast, the solid formed by stacking squares has a more uniform and boxy appearance due to the congruence of the squares.
What is the integral evaluated to calculate the volume of the solid formed by stacking squares on the curve y = e^x from x = 0 to x = 2?
-The integral is e^(2x) with respect to x, evaluated from 0 to 2. After substitution (u = 2x, du = 2dx), it simplifies to (1/2) * e^u du, which is then evaluated from 0 to 4, resulting in (e^4 - 1)/2.
What is the general approach to calculating the volume of a solid formed by any cross-sectional shape?
-The general approach involves determining the area of the cross-sectional shape at each point along the axis of integration, and then integrating this area with respect to the variable representing the axis, within the specified bounds.
Why is it important to remember the specific formula for the area of a semicircle when calculating the volume of a solid formed by stacking semicircles?
-It is important because the area of a semicircle is half the area of a full circle, and using the incorrect area (e.g., that of a full circle) would lead to an incorrect volume calculation. The formula for the area of a semicircle is π/2 times the square of the radius.
How does the script demonstrate the process of learning and applying mathematical concepts?
-The script demonstrates the process by first introducing the concept of creating solids through cross-sectional areas, then progressively building up to more complex shapes (squares, semicircles, equilateral triangles), and finally applying integration to calculate the volume of these solids. It emphasizes the importance of understanding the underlying geometry and algebra, and provides shortcuts like formulas to aid in calculations.
Outlines
📐 Introduction to Calculating Solid Volumes with Cross-Sections
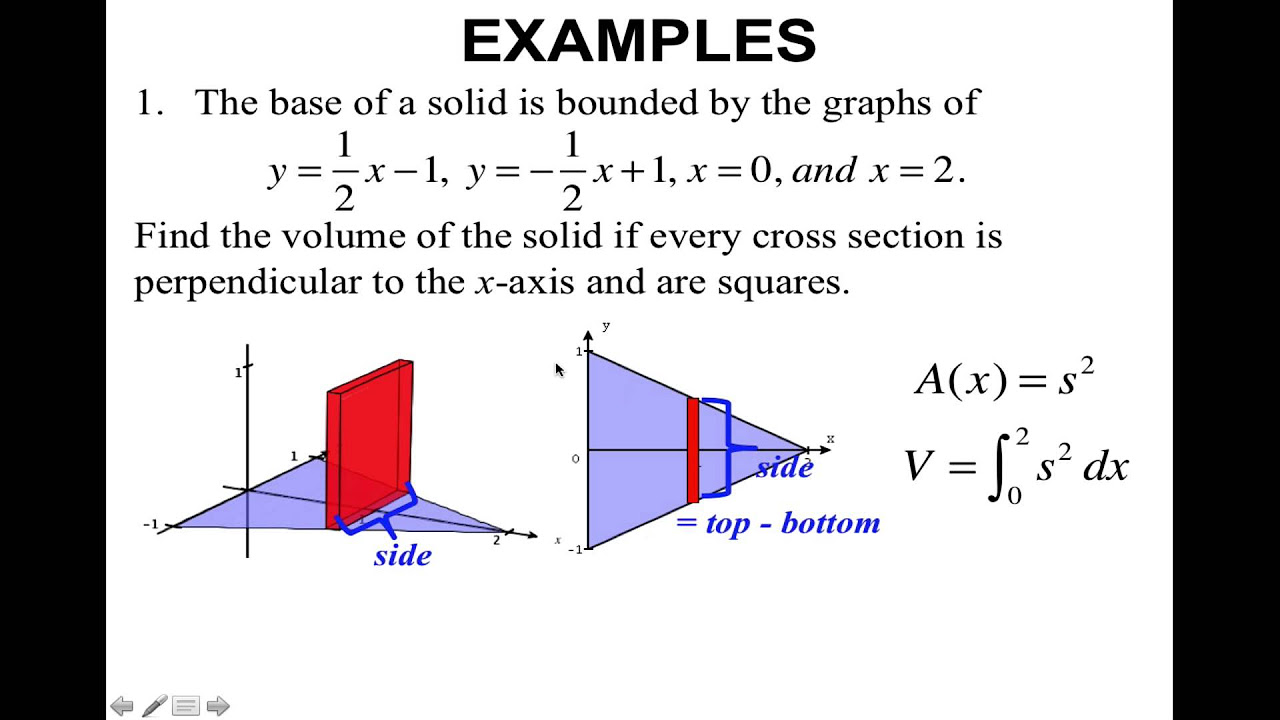
The video begins with Mr. R discussing the concept of calculating the volumes of solids formed by known cross-sections. He uses the graph of y = x^2 and y = x to illustrate how revolving these around the x-axis or y-axis can create a solid of revolution. He then introduces an alternative method, which involves building on top of the intersection of the curves using squares, creating a different solid. The video aims to explore this method and others using cross-sectional areas.
🛠️ Solid Volume Calculation Using Square Cross-Sections
Mr. R explains how to calculate the volume of a solid formed by stacking squares on top of cross-sections created by the graph of y = e^x and y = x^0 (y = 1) for x ranging from 0 to 2. He demonstrates that the side length of each square is e^x and thus the area of each square is e^(2x). The volume of the solid is found by integrating the area of these squares with respect to x from 0 to 2, resulting in a straightforward integral to solve.
📉 Volume Calculation with Semicircles and the Difference of Functions
The video moves on to using semicircles to build a solid when the cross-sections are perpendicular to the x-axis. Mr. R uses the functions y = 2x and y = x^2, finding the difference between them to establish the diameter of the semicircles. He simplifies the expression for the area of the semicircles and shows how to integrate this expression from 0 to 2 to find the volume of the solid formed by the semicircles.
🔺 Constructing Solids with Equilateral Triangle Cross-Sections
Mr. R explores the use of equilateral triangles to form a solid when the cross-sections are perpendicular to the x-axis. He uses the function y = e^x and y = x^0 (y = 1) for x ranging from 0 to 1. He explains how to find the area of an equilateral triangle using the side length e^x and the altitude derived from the Pythagorean theorem. The area of each triangle is then integrated from 0 to 1 to find the volume of the solid.
🧮 Final Thoughts on Cross-Sectional Volume Calculations
In the concluding part, Mr. R summarizes the process of calculating the volume of solids using different cross-sectional shapes like squares, semicircles, and equilateral triangles. He emphasizes that the key is to determine the area of one of these shapes based on the given functions and then integrate that area along the appropriate axis and within the correct bounds. He encourages viewers to practice these methods and offers help for any further questions.
Mindmap
Keywords
💡Solids of Revolution
💡Cross-Sectional Area
💡Integration
💡Exponential Function
💡Square Cross-Sections
💡Semicircles
💡Equilateral Triangles
💡Graphs
💡Volume Calculation
💡GeoGebra
💡Binomial Squaring
Highlights
Mr. R discusses calculating volumes of solids formed by known cross-sections, a common topic in calculus and AP exams.
Solids can be formed by revolving regions around the x-axis, y-axis, or any random axis, creating solids of revolution.
An alternative method to revolving is building on top of the region with shapes like squares, creating a different kind of solid.
Demonstrates using Geogebra to visually show how squares can be built on top of a cross-section to form a solid.
Introduces the concept of cross-sectional area with squares as the first example, perpendicular to the XY plane.
Explains how the size of the squares changes as the cross-section moves along the curve, affecting the volume of the solid.
Illustrates the process of adding more squares to approximate the solid's shape, resulting in an interesting crooked form.
Presents the integral calculation for the volume of the solid formed by squares using the function y = e^x from x=0 to x=2.
Shows how to use substitution in integration to simplify the calculation of the solid's volume.
Introduces the use of semicircles for cross-sections as an alternative to squares, with a focus on the difference in functions determining the diameter.
Demonstrates building a solid with semicircles using the functions y = 2x and y = x^2, and how their difference forms the semicircles' diameters.
Explains the integration process for the area of semicircles to find the volume of the solid, resulting in a volume of 2π/15.
Discusses the use of equilateral triangles for cross-sections, a less common but still valid method for calculating volumes.
Provides a geometry refresher on equilateral triangles, including the use of the Pythagorean theorem to find the height.
Derives the area formula for an equilateral triangle using the side length and the square root of 3 over 4.
Applies the area formula for equilateral triangles to the function y = e^x to find the volume of the solid formed.
Integrates the area of equilateral triangles from x=0 to x=1 to find the volume, resulting in a volume of √3/8 * (e^2 - 1).
Encourages memorization of the area formulas for efficiency, but also demonstrates how to derive them during the problem-solving process.
Stresses the flexibility in choosing cross-sectional shapes, such as rectangles, trapezoids, or right triangles, for volume calculations.
Concludes with encouragement and an offer to answer questions, highlighting the importance of understanding the process over memorization.
Transcripts
Browse More Related Video
Topic 43-Volumes of Solids with Known Cross Sections

Volume of Solids with Known Cross Sections

Volume Using Known Cross Sections (Slicing) | Calculus 2 Lesson 5 - JK Math

Calculus AB/BC – 8.7 Volumes with Cross Sections: Squares and Rectangles

Calculus Integrals for Volumes with Known Cross Sections

Finding the Volumes of Known Cross Sections ❖ AP Calculus AB
5.0 / 5 (0 votes)
Thanks for rating: