Calculus 1 Lecture 5.2: Volume of Solids By Disks and Washers Method
TLDRThe video script is an in-depth exploration of calculating the volume of various three-dimensional shapes using the method of discs and washers. The presenter begins by introducing the concept of slicing a solid figure into thin slabs to approximate its volume, drawing parallels with the area under a curve in calculus. The discussion then delves into the specifics of finding the volume of solids of revolution, where the cross-sectional area of a shape revolved around an axis forms a circle. The presenter explains that the volume can be found by integrating the cross-sectional area from one point to another along the axis of rotation. The method of discs is used for solids without a hole, while the method of washers is introduced for those with a hole in the middle. The script provides a step-by-step approach to setting up and solving integrals for both methods, emphasizing the importance of correctly identifying the functions and bounds for integration. The presenter also highlights the need to adapt the method when revolving around different axes, specifically the x-axis or y-axis, and provides examples to illustrate the process. The summary concludes with a more complex problem involving a solid contained between two functions revolved around a line that is not an axis, which requires a modification of the existing formula. The video is educational, providing clear explanations and examples to help viewers understand the application of calculus in calculating volumes of complex shapes.
Takeaways
- 📐 The concept of finding the volume of certain 3D figures using the method of discs and washers is introduced, which involves integrating the area of cross-sections.
- 🔄 The method is applicable to solids of revolution, where a 2D shape is rotated around an axis to form a 3D object.
- ⭕️ Cross-sections of the solid, when rotated around an axis, are typically in the shape of circles, and the radius of these circles corresponds to the height of the function at a given point.
- 📈 The volume is calculated by integrating the difference in the areas of the outer and inner circles (for washers) or just the area of the circles (for discs) from one limit to another.
- 🎢 For a solid generated by revolving a function around the x-axis, the bounds of integration are determined by the x-values where the function intersects with the axis or another function.
- 🔢 The actual calculation involves squaring the function values, as the area of a circle is π times the radius squared, and then integrating over the interval defined by the bounds.
- 🔽 When dealing with functions that have a hole in the middle (like a vase), the method of washers is used, which involves subtracting the area of the inner function from the outer function before integrating.
- 🤔 Determining which function is the outer and which is the inner one is crucial for setting up the integral correctly and ensuring the volume calculated is positive.
- 📉 The process requires algebraic manipulation and solving for the variable in terms of the axis around which the solid is being revolved.
- 🧮 The calculation involves careful consideration of the limits of integration and the correct setup of the integral, including distributing constants and combining like terms.
- 📝 It is emphasized that setting up the integral correctly is often more challenging than the integration itself, and students are encouraged to practice to become comfortable with the process.
Q & A
What is the method of discs and washers used for in calculus?
-The method of discs and washers is used in calculus to find the volume of a solid of revolution, which is created when a region between two curves on a plane is rotated around a given axis.
How does the method of slicing relate to finding the volume of a solid?
-The method of slicing involves dividing the solid into infinitesimally thin slices and finding the volume of each slice. The total volume is then obtained by integrating the sum of these slices, which is analogous to finding the area under a curve using definite integrals.
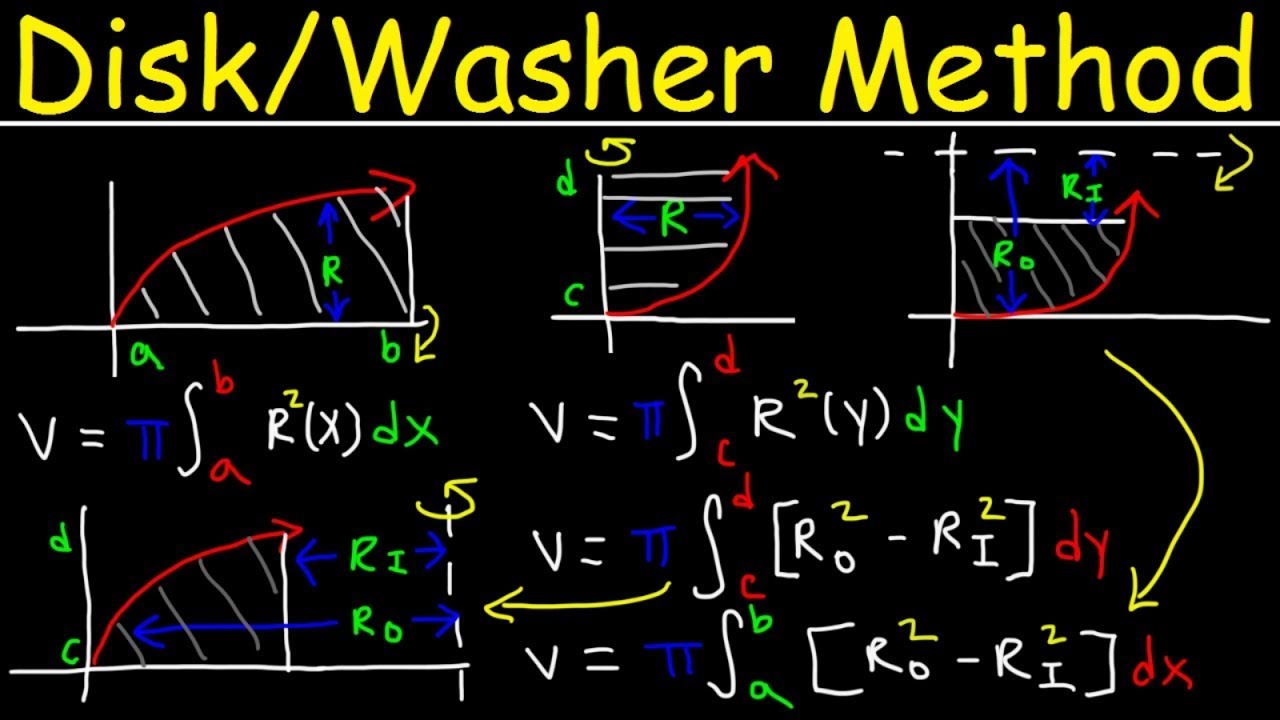
What is the general formula for finding the volume of a solid using the method of discs?
-The general formula for the volume using the method of discs is V = π * ∫[a, b] (R(x)^2 - r(x)^2) dx, where R(x) is the radius of the outer circle and r(x) is the radius of the inner circle at a given x value within the interval [a, b].
What is the difference between the method of discs and the method of washers?
-The method of discs is used when the solid has a uniform cross-sectional shape, like a cylinder, while the method of washers is used when the solid has a hole in the middle, creating an annular cross-section. The method of washers involves subtracting the area of the inner circle from the area of the outer circle to find the area of the washer.
How does the choice of the axis of rotation affect the volume calculation?
-The choice of the axis of rotation significantly affects the volume calculation. If the solid is rotated around an axis that is not perpendicular to the planes of the solid, the method of discs and washers may not be applicable. The axis must be chosen such that the cross-sections are circular and perpendicular to the axis of rotation.
What is the role of the arbitrary point in the method of discs and washers?
-The arbitrary point is used to find the cross-sectional area at a specific location within each subinterval of the solid. As the number of subintervals increases and their width approaches zero, the arbitrary point allows for the accurate approximation of the cross-sectional area, which is crucial for the integral calculation of the volume.
What is the significance of the radius in the context of the method of discs and washers?
-The radius is the distance from the axis of rotation to the curve defining the boundary of the solid. It is used to calculate the area of the cross-sectional circles (discs or washers) at each slice. The radius can vary along the axis of rotation, and its value at any point is given by the height of the function at that point.
How does the shape of the cross-section affect the volume calculation?
-The shape of the cross-section directly affects the volume calculation because the volume is found by integrating the surface area of the cross-sections. If the cross-section is circular, as in the method of discs and washers, the area is calculated using πr^2, where r is the radius. If the cross-section has a different shape, a different formula would be required to calculate the area.
What is the role of limits in the method of discs and washers?
-Limits are used to transition from an approximation of the volume, which involves a finite number of slices, to an exact volume. By taking the limit as the number of slices approaches infinity, the width of each slice approaches zero, which allows for the precise calculation of the volume through the definite integral.
Can the method of discs and washers be applied to any solid of revolution?
-The method of discs and washers can be applied to a wide variety of solids of revolution, but it is primarily used when the solid is generated by revolving a region around an axis that is perpendicular to the cross-sections. If the axis of rotation is not perpendicular to the cross-sections, or if the cross-sections are not circular, alternative methods may be needed.
What is the process for setting up an integral to find the volume of a solid of revolution using the method of discs and washers?
-To set up an integral for the volume of a solid of revolution using the method of discs and washers, one must first determine the interval of integration (a to b), identify the outer and inner radii functions (R(x) and r(x)), set up the integral using the formula V = π * ∫[a, b] (R(x)^2 - r(x)^2) dx, and finally evaluate the integral to find the volume.
Outlines
📚 Introduction to Volume Calculation with Discs and Washers
The paragraph introduces the concept of calculating the volume of certain geometric figures using the method of discs and washers. It draws an analogy with the area under a curve and emphasizes the importance of understanding the foundational idea rather than just memorizing formulas. The method involves slicing a solid figure into thin slabs and summing their volumes to approximate the total volume.
🏗️ Building Up the Concept of Volume Calculation
This section delves deeper into the process of finding the volume of a solid by slicing it into thin slabs. It explains that the volume of each slab can be approximated by multiplying its cross-sectional area by its width. The process is likened to finding the area of rectangles in a previous example, with the volume being the three-dimensional equivalent.
📏 Cross-Sectional Area and the Volume of a Rectangular Prism
The paragraph discusses how to calculate the volume of a basic shape like a rectangular prism and extends this concept to more complex shapes. It highlights that the volume is typically the product of the cross-sectional area and the length of the slab, emphasizing the need to find the area of the cross-section for irregular shapes.
🚀 Application of the Method to Solids with Slabs Perpendicular to the x-axis
The focus here is on applying the volume calculation method to solids where the sides are perpendicular to the x-axis. It is clarified that this method is not applicable to all solids and that certain conditions must be met, specifically that the planes of the solid are perpendicular to the x-axis.
🔍 Detailed Examination of the Slicing Process
This paragraph provides a detailed look at the slicing process, emphasizing the width of the slabs and how an arbitrary point within each slab is chosen to find the cross-sectional area. It also touches on the concept of limits as the number of slabs approaches infinity, leading to a more precise volume calculation.
🔢 Volume Calculation through Integration
The paragraph explains how to find the volume of a solid by integrating the cross-sectional area from a starting point A to an ending point B. It is clarified that the arbitrary point chosen within each slab allows for the calculation of the cross-sectional area, which is then multiplied by the width (Delta X) of the slab to approximate the volume.
🎨 Visualizing the Method of Discs and Washers
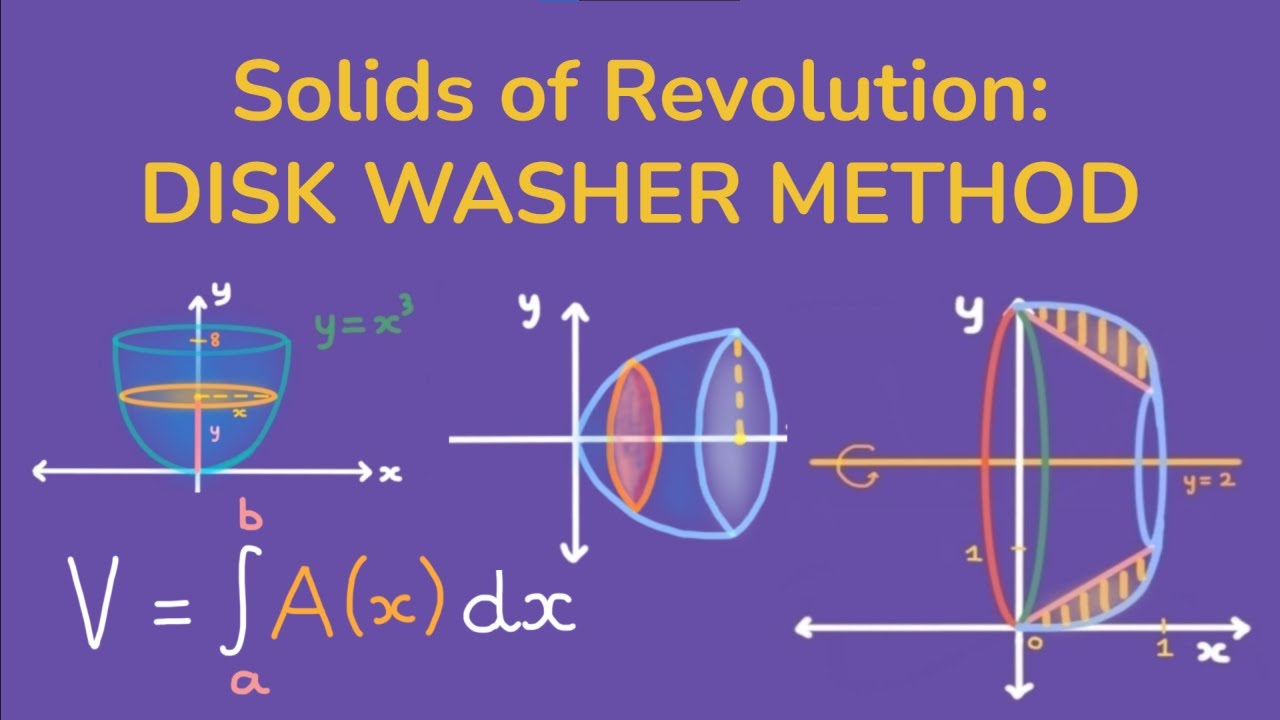
The discussion moves to the method of discs and washers, which is used when the solid is created by revolving a shape around an axis. The paragraph illustrates how the cross-sectional shape is always a circle when revolving around a perpendicular axis, and the radius of this circle corresponds to the height of the original function at a given point.
🌀 Revolution of Solids and the Resulting Volume
This section explores the concept of a solid of revolution, which is created by revolving a shape around an axis. Examples given include revolving a rectangle to form a cylinder, a circle to form a sphere, and a half-sphere to form a complete sphere. The paragraph emphasizes the importance of understanding the shape being revolved and the axis of revolution.
🧮 Setting Up the Integral for Volume Calculation
The paragraph provides a step-by-step guide on setting up the integral for calculating the volume of a solid of revolution. It emphasizes the need to identify the correct function, the interval over which to integrate, and how to express the volume as an integral involving pi and the squared function value.
📏 Cross-Sectional Area and the Method of Washers
The discussion focuses on the method of washers, which is used when there are two functions involved, creating a hole in the middle of the solid. The paragraph explains how to find the volume by subtracting the area of the inner function's cross-section from the outer function's cross-section and then integrating this difference over the interval.
📐 Determining the Functions and Intervals for Volume Calculation
This section emphasizes the importance of correctly identifying the top and bottom functions as well as the interval over which they are being integrated. It also touches on the concept of setting the functions equal to each other to find the points of intersection, which helps in determining the limits of integration.
🧷 Integration and Evaluation of the Volume
The paragraph concludes with the actual integration and evaluation of the volume. It provides a clear example of how to carry out the integration, emphasizing the importance of correctly applying the limits of integration and the need to be mindful of the order of operations and algebraic manipulations.
Mindmap
Keywords
💡Volume
💡Discs and Washers
💡Integration
💡Solid of Revolution
💡Cross-Sectional Area
💡Cylinder
💡Sphere
💡圆锥 (Cone)
💡Method of Slicing
💡Arbitrary Point
💡Definite Integral
Highlights
The concept of finding the volume of certain figures using the method of discs and washers is introduced.
The method of slicing a figure into thin slabs is analogous to finding areas under a curve, but extended to three dimensions for volume calculations.
The importance of the figure being a solid with no holes through the middle for the volume calculation method to apply is emphasized.
The volume of a slice is found by multiplying the cross-sectional area by its width, which parallels the area under a curve concept.
The cross-sectional area times the width (or length) of the slab gives a good approximation of the volume, which becomes exact as the width approaches zero.
The method is applicable for solids bounded by planes perpendicular to the x-axis, allowing for the calculation of volume through integration.
An arbitrary point within each interval is chosen to find the cross-sectional area for the volume approximation.
The process of taking the limit as the number of slabs approaches infinity transforms the approximation into an exact volume calculation.
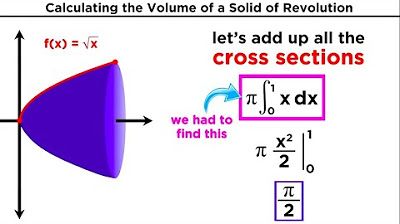
The volume of a solid of revolution can be found by integrating the cross-sectional area from a starting point A to an ending point B.
The method of discs is applicable when the cross-sectional shape is a circle, which is always the case when revolving around the x-axis.
The radius of the cross-section in a solid of revolution equals the function's height at any given point x, making the function equal to the radius.
The method of washers is introduced for calculating the volume of a solid with a hole in the middle, such as when revolving an area between two functions around an axis.
The volume by washers formula involves subtracting the area of a smaller circle (made by the lower function) from the area of a larger circle (made by the upper function).
The process of setting up and evaluating the integral for the volume of a solid of revolution, including handling the pi constant, is demonstrated with examples.
The importance of determining which function is on top and on the bottom for the interval of integration is stressed to avoid incorrect volume calculations.
The method of cylindrical shells, an alternative to discs and washers, is mentioned as a different approach to finding volumes, which will be discussed in the next section.
A comprehensive example of finding the volume of a solid created by revolving a specific function around the x-axis is provided, including the setup, evaluation, and interpretation of the result.
The difference in volume calculation when revolving the same shape around different axes (x-axis vs. y-axis) is explored, highlighting the need to adjust the setup accordingly.
The necessity to express functions in terms of the axis around which the solid is being revolved (x for x-axis, y for y-axis) is clarified for both the method of discs and washers and the upcoming cylindrical shells method.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: