Calculus AB Homework 7.5 Shell Method

Michelle Krummel

20 Mar 201815:05

EducationalLearning

32 Likes 10 Comments

TLDRThis instructional video guides viewers through solving problems 42 to 46 from a calculus unit, focusing on finding the volume of solids of revolution using the shell method. The script covers various regions, including those bounded by functions like y=1-x, y=√x, and y=x^2, and demonstrates the process of rotating these regions around different axes. Each problem is methodically worked through, integrating the appropriate expressions to calculate the volume of the resulting cylindrical shells, leading to final answers such as π/3 and 16π/3.

Takeaways

📚 The video is a tutorial on solving calculus problems involving the volume of solids of revolution using the shell method.
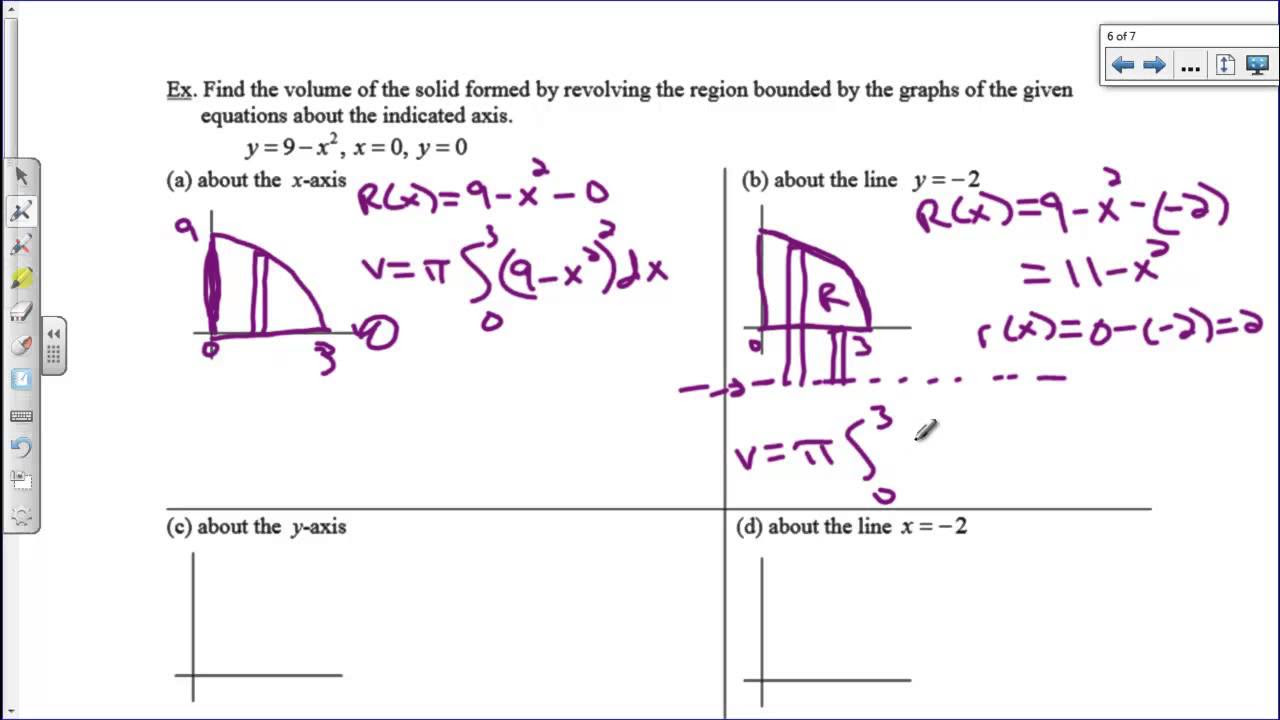
📐 Problem 42 involves a region bounded by the curves y=1-x, y=0, and x=0, rotated around the y-axis to form cylindrical shells.
🔍 The radius of the cylindrical shell in Problem 42 is determined by the horizontal distance x, and the height is given by the vertical distance y=1-x.
🧮 The integral for Problem 42 is set up as 2π times the integral from 0 to 1 of x(1-x) dx, resulting in a volume of π/3.
🌐 Problem 43 rotates the region bounded by y=√x, y=0, and x=4 around the y-axis, with the radius of the shell being x and the height √x.
📉 The integral for Problem 43 is 2π times the integral from 0 to 4 of x^(3/2) dx, leading to a volume of 128π/5.
🔄 Problem 44 rotates the region bounded by y=x^2, y=0, and x=2 around the y-axis, with the radius being x and the height x^2.
📈 The integral for Problem 44 is 2π times the integral from 0 to 2 of x^3 dx, yielding a volume of 8π.
🔄 Problem 45 involves a more complex region bounded by two parabolas, rotated around the line x=2, with the radius being 2-x and the height given by the difference of the two parabolas.
📘 The integral for Problem 45 is 2π times the integral from 0 to 2 of (4x - x^2)(2-x) dx, resulting in a volume of 16π/3.
📘 Problem 46 rotates the region bounded by y=1/x between y=1 and y=2 around the x-axis, with the radius being y and the height being 1/y.
📊 The integral for Problem 46 is 2π times the integral from 1 to 2 of 1 dy, giving a final volume of 2π.

Q & A

What is the main topic of the video?
-The video is about solving unit 7 homework problems 42 through 46, which involve finding the volume of a solid of revolution using the shell method.
What is the first region described in the video and around which axis is it rotated?
-The first region is formed by the equations y = 1 - x, y = 0, and x = 0, and it is rotated around the y-axis.
Why is the first problem considered a DX problem?
-The first problem is a DX problem because the reference rectangle is vertical and parallel to the y-axis, which is the axis of rotation.
How is the radius of the cylindrical shell determined in the first problem?
-The radius of the cylindrical shell in the first problem is determined by the horizontal distance, which is simply x, from the y-axis to the curve y = 1 - x.
What is the integral set up for the volume of the solid in the first problem?
-The integral set up for the volume of the solid in the first problem is 2π times the integral from 0 to 1 of x(1 - x) dx.
What is the final answer for the volume of the solid in the first problem?
-The final answer for the volume of the solid in the first problem is π/3.
What are the equations defining the region for problem 43, and around which axis is it rotated?
-The region for problem 43 is defined by y = √x, y = 0, and x = 4, and it is rotated around the y-axis.
How is the height of the cylindrical shell determined in problem 43?
-The height of the cylindrical shell in problem 43 is determined by the vertical distance, which is √x, from the bottom of the rectangle (y = 0) to the top (y = √x).
What is the integral set up for the volume of the solid in problem 43?
-The integral set up for the volume of the solid in problem 43 is 2π times the integral from 0 to 4 of x * (√x) dy.
What is the final answer for the volume of the solid in problem 43?
-The final answer for the volume of the solid in problem 43 is 128π/5.
What is the difference between a DX problem and a DY problem in the context of the shell method?
-In a DX problem, the reference rectangle is vertical and parallel to the axis of rotation, and the integration is with respect to x. In a DY problem, the reference rectangle is horizontal and the integration is with respect to y.
For problem 46, what is the region being rotated around the x-axis, and what are the equations defining it?
-In problem 46, the region being rotated around the x-axis is enclosed by y = 1/x and y = 2, with x = 0 as the lower limit.
How is the radius of the cylindrical shell determined in problem 46?
-The radius of the cylindrical shell in problem 46 is determined by the vertical distance, which is y, from the x-axis to the curve y = 1/x.
What is the integral set up for the volume of the solid in problem 46?
-The integral set up for the volume of the solid in problem 46 is 2π times the integral from 1 to 2 of y * (1/y) dy.
What is the final answer for the volume of the solid in problem 46?
-The final answer for the volume of the solid in problem 46 is 2π.

Outlines

00:00

📚 Volume of Solids via Shell Method: Homework Problems 42-46

This paragraph introduces a series of calculus homework problems focusing on finding the volume of solids of revolution using the shell method. The problems involve rotating regions bounded by specific equations around the y-axis. The first problem, number 42, revolves around the region formed by y=1-x, y=0, and x=0. The process involves setting up a reference rectangle parallel to the axis of rotation, identifying the points of intersection, and integrating the product of the radius and height of the resulting cylindrical shell from 0 to 1. The final result for this problem is π/3. The explanation also outlines the process for problem 43, which involves rotating around the y-axis a region bounded by y=√x, y=0, and x=4, and provides a step-by-step integration approach to find the volume.

05:00

📐 Rotating Regions Around the Y-Axis for Volume Calculation

The second paragraph continues the discussion on calculating volumes of solids of revolution using the shell method, focusing on problems involving rotation around the y-axis. It details the process for finding the volume of a solid formed by rotating the region bounded by y=x^2, y=0, and x=2. The explanation involves drawing a vertical rectangle as the reference for the shell, calculating the radius and height of the cylindrical shell, and integrating the expression X^3 from 0 to 2. The result for this problem is 8π. The paragraph also begins to address problem 45, which involves a more complex region bounded by two parabolas and a vertical line, x=2, requiring the identification of points of intersection and a careful setup for the integral.

10:02

🔍 Advanced Shell Method Application: Rotating Complex Regions

The third paragraph delves into the complexities of the shell method when rotating regions defined by multiple equations around an axis. It discusses problem 45, which involves rotating the region between two parabolas and a vertical line, x=2, around the same line. The explanation includes finding the points of intersection between the equations y=4x-x^2 and y=x^2, setting up the integral with respect to x, and integrating the expression 4x-2x^2 from 0 to 2. The result for this problem is 16π/3. The paragraph also introduces problem 46, which requires rotating a region bounded by y=1/x between y=1 and y=2 around the x-axis, marking a shift from dy to dx in the integration process, and concludes with the setup for the integral of 1 with respect to y from 1 to 2, yielding a final volume of 2π.

Mindmap

Keywords

💡Solid of Revolution

A solid of revolution is a three-dimensional object created by rotating a two-dimensional shape, called a 'profile', around a line called the 'axis of rotation'. In the video, the theme revolves around finding the volume of various solids of revolution using the shell method, which is a mathematical technique for calculating the volume of such solids.

💡Shell Method

The shell method is a technique used to find the volume of a solid of revolution by considering cylindrical shells created by rotating an infinitesimally small 'slice' of the solid around the axis of rotation. The video script describes how to apply this method to different mathematical functions to calculate their volumes when rotated around the y-axis or x-axis.

💡Volume

Volume refers to the amount of space occupied by a solid object. In the context of the video, the volume is calculated for different solids of revolution, which involves integrating the area of the profile over the interval of rotation to find the total space enclosed by the solid.

💡Integration

Integration is a fundamental concept in calculus that represents the process of finding a function's integral to determine quantities such as area, volume, or accumulated values. In the video, integration is used to calculate the volume of the cylindrical shells that make up the solid of revolution.

💡Cylindrical Shell

A cylindrical shell is a geometric shape that results from rotating a rectangle around an axis perpendicular to one of its sides. In the video, the concept of cylindrical shells is central to the shell method, where the volume of each shell is calculated and then integrated over the interval of rotation.

💡Radius

In the context of the video, the radius of a cylindrical shell is the distance from the axis of rotation to the edge of the shell. The radius is a key component in calculating the volume of each shell, as it determines the size of the cylinder.

💡Height

The height of a cylindrical shell in the video refers to the vertical distance between the top and bottom of the shell, which is used to calculate the volume of the shell. It is the difference in the y-values of the function at the limits of integration.

💡DX Problem

A DX problem in the context of the video indicates that the integration is with respect to the x-variable, and the equations need to be solved for y in terms of x. This is important for setting up the integrals correctly when using the shell method to find volumes.

💡Points of Intersection

Points of intersection are the x-values where two functions or a function and the axis intersect within the region of interest. In the video, these points are crucial for determining the limits of integration when calculating the volume of the solid of revolution.

💡Antiderivative

An antiderivative is a function that represents the reverse process of differentiation. In the video, antiderivatives are found for the functions describing the profile of the solid of revolution to calculate the volume of the cylindrical shells.

💡Common Denominator

A common denominator is a single denominator that can be used for two or more fractions, allowing for their combination or comparison. In the video, finding a common denominator is part of the process of simplifying the expression obtained after integrating, to find the final volume of the solid.

Highlights

Introduction to solving unit 7 homework problems 42 through 46 using the shell method for solids of revolution.

Explanation of setting up a reference rectangle for the shell method parallel to the axis of rotation.

Clarification that the problems are DX problems, requiring integration with respect to X.

Description of the region formed by the equations y=1-x, y=0, and x=0, and its rotation around the y-axis.

Calculation of the volume of a cylindrical shell resulting from the rotation, with the radius being X and height being y=1-x.

Integration process from 0 to 1 to find the volume of the solid, resulting in the answer π/3.

Problem 43 involves a region formed by y=√x, y=0, and x=4, rotated around the y-axis.

Method for finding the radius and height of the cylindrical shell for problem 43, with the radius being X and height being √x.

Integration of X^(3/2) from 0 to 4 to calculate the volume, yielding a result of 128π/5.

Problem 44's region is defined by y=x^2, y=0, and x=2, with rotation around the y-axis.

Setup for the volume calculation in problem 44, with the radius as X and height as x^2.

Integration of X^3 from 0 to 2, resulting in a final volume of 8π.

Problem 45 involves finding the volume of a solid from the rotation of two parabolas around the line x=2.

Determination of the points of intersection for the parabolas in problem 45, which are x=0 and x=2.

Integration of the expression 4x - 2x^2 + 2x^3 from 0 to 2 for problem 45's volume calculation.

Final volume calculation for problem 45, resulting in 16π/3.

Problem 46 uses the shell method to find the volume of a solid from the rotation of y=1/x around the x-axis.

Transformation of the equation y=1/x to x=1/y for the shell method in problem 46.

Integration of 1 with respect to Y from 1 to 2 to find the volume, concluding with 2π as the final answer.

Transcripts

Browse More Related Video

Calculus AB Homework 7.4 Disk and Washer Method

Calculus 1: Shell Method Examples

Volume The Disc Method

Disc/Washer Method vs. Shell Method (rotated about different lines)

Calculating Volume by Cylindrical Shells

Solid of Revolution (part 5)

Calculus AB Homework 7.5 Shell Method

Takeaways

Q & A

What is the main topic of the video?

What is the first region described in the video and around which axis is it rotated?

Why is the first problem considered a DX problem?

How is the radius of the cylindrical shell determined in the first problem?

What is the integral set up for the volume of the solid in the first problem?

What is the final answer for the volume of the solid in the first problem?

What are the equations defining the region for problem 43, and around which axis is it rotated?

How is the height of the cylindrical shell determined in problem 43?

What is the integral set up for the volume of the solid in problem 43?

What is the final answer for the volume of the solid in problem 43?

What is the difference between a DX problem and a DY problem in the context of the shell method?

For problem 46, what is the region being rotated around the x-axis, and what are the equations defining it?

How is the radius of the cylindrical shell determined in problem 46?

What is the integral set up for the volume of the solid in problem 46?

What is the final answer for the volume of the solid in problem 46?