2021 Live Review 8 | AP Calculus AB | Reviewing Multiple-Choice & Free-Response Questions

The speaker, Mark, expresses enthusiasm for the final session of a course and welcomes everyone. He outlines the day's plan, which includes discussing the exam format, providing a mini mock exam, and addressing feedback from participants. The exam details are shared, including dates, format (paper and pencil or digital), and the structure of the test, which consists of multiple-choice and free-response questions. Mark also emphasizes the importance of practicing traditional exam formats and using the provided resources, such as a Dropbox link and QR code.

Mark presents a calculus warm-up problem involving the integration of continuous functions g and h. He guides the audience through solving the problem step by step, emphasizing the importance of understanding the bounds of integration and the concept of integrating a constant. The correct answer is identified as option B, and Mark cautions against common mistakes such as not accounting for the bounds correctly. He also touches on the difference between integrating sums/differences and products/quotients.

The session continues with a mini mock exam that is not in the full format but covers various topics. Mark encourages students to pause the video and work through the problems, which include a mix of odd and even numbered questions. He mentions that full annotated solutions will be available and discusses the importance of reviewing previous videos for a comprehensive understanding. The focus is on practicing and understanding calculus problems, with an emphasis on the learning journey rather than just the exam.

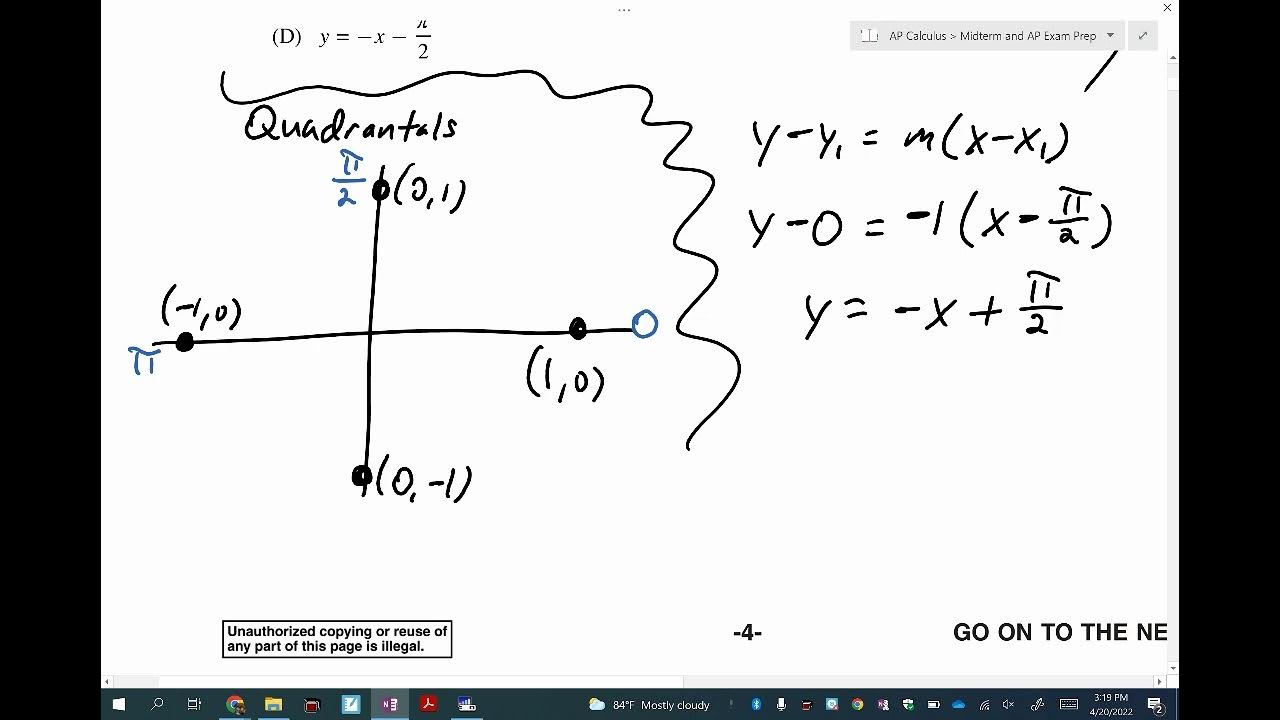
Mark works through a problem involving a piecewise function f, which is defined differently for x ≤ -1 and x > -1. He discusses the conditions for the function to be continuous and differentiable, which leads to solving for the parameters m and k. The problem involves finding the slope of the tangent line at a specific point, which requires taking the derivative of the function and applying the given conditions.

The paragraph deals with evaluating the behavior of a function h with given select values and critical points. Mark discusses the implications of critical points and inflection points on the function's graph. He eliminates certain answer choices based on the information provided and the properties of the function. The discussion involves understanding the relationship between the function's values, its critical points, and the overall trend of the function within a given interval.

Mark explores the concept of slope fields for differential equations. He examines a given differential equation and identifies the slope field that corresponds to it. The process involves analyzing the equation's zeros and the behavior of the slope function. Mark also discusses how to confirm the correct slope field by checking the behavior of the function, such as its increasing and decreasing intervals.

In this part, Mark is given the graph of the derivative of a function g and must determine which of the provided graphs could represent the function g itself. He analyzes the behavior of g' to infer the behavior of g, considering aspects such as increasing and decreasing intervals, as well as concavity. Mark uses the information to eliminate impossible options and identify the correct graph for g.

Mark introduces the concept of the 'yellow sheet,' a personalized formula sheet for studying. He emphasizes the importance of creating one's own sheet to review necessary formulas for the AP Calculus exam. Although the yellow sheet cannot be used during the exam, it serves as a valuable study tool. Mark also humorously mentions that the sheet could be used for constant review, even in unconventional places like the bathroom mirror.

Mark tackles a differential equation problem, providing a step-by-step solution. He starts by finding the equation of the tangent line to a function f at x = 2 and then uses it to approximate the value of f at x = 1.9. The process involves understanding the concept of derivatives as slopes and applying the tangent line equation. Mark also discusses the implications of the second derivative on the accuracy of the approximation.

The paragraph deals with the analysis of overestimates and underestimates in the context of calculus problems. Mark calculates the second derivative of a function and uses its sign to determine whether an approximation is an overestimate or an underestimate. He explains the concept of concavity and how it relates to the shape of the function's graph, providing a clear understanding of why the approximation is either too high or too low.

Mark completes the solution to the given differential equation, applying algebraic techniques to isolate y and express it as a function of x. He emphasizes the importance of simplifying the equation according to the problem's requirements. Mark also reflects on the progress students have made in their calculus journey, highlighting their improved algebraic skills and the challenges they've overcome. He encourages students to continue challenging themselves and helping others.

In the final paragraph, Mark and his co-host share words of encouragement and advice for students preparing for exams. They stress the importance of viewing tests as a measure of knowledge on a specific day, rather than a measure of self-worth. The hosts provide takeaways that emphasize the students' growth as mathematicians and the value of making mistakes as part of the learning process. They also mention the availability of answer keys and additional practice circuits for continued study and improvement.