AP Calculus: EVERYTHING YOU NEED TO KNOW
TLDRThis video script is a comprehensive study guide for the AP Calculus AB and BC exams, covering essential topics from algebra and precalculus foundations to advanced calculus concepts. The speaker emphasizes memorization of derivatives, integrals, and key calculus theorems, while also discussing problem-solving strategies for rates of change, optimization, and motion problems. Additionally, the script touches on series, convergence tests, and Taylor series, aiming to prepare students for both multiple-choice and free-response sections of the exam. The speaker concludes with encouragement, reminding students that their worth is not defined by their AP exam scores.
Takeaways
- 📚 The video is a comprehensive review for the AP Calculus AB and BC exams, aimed at helping students identify critical topics and areas for focused study.
- 🎓 The presenter emphasizes the importance of understanding algebra concepts, such as point-slope form and completing the square, as a foundation for calculus.
- 📈 The video covers a wide range of calculus topics, including limits, derivatives, integrals, and applications of derivatives, which are essential for the AP exam.
- 📉 The presenter introduces and explains various calculus rules and theorems, such as the chain rule, product rule, quotient rule, and l'Hôpital's rule, which are necessary for solving calculus problems.
- 📈 The importance of memorizing basic derivatives and integrals is highlighted, as these are frequently used throughout the AP exam.
- 📚 The video provides strategies for tackling different types of calculus problems, such as related rates, optimization, and motion problems, which are integral to the AP curriculum.
- 📝 The presenter suggests using resources like handouts and PowerPoint presentations to aid in studying and understanding complex calculus concepts.
- 🔍 The video touches on the use of calculators for solving systems of equations and emphasizes the importance of knowing when calculators are not necessary for certain problems.
- 📉 The presenter explains how to analyze the graph of a function using derivatives, including finding increasing/decreasing intervals, concavity, and critical and inflection points.
- 📝 The video concludes with encouragement for students, reminding them that their worth is not defined by their AP exam scores and to maintain a positive outlook on their abilities and future.
- 🔍 For AP Calculus BC students, additional topics such as integration by parts, improper integrals, series, and vector-valued functions are discussed, which are beyond the scope of AP Calculus AB.
Q & A
What is the main purpose of the video?
-The main purpose of the video is to provide a comprehensive review of AP Calculus AB and BC topics, focusing on the most critical information needed for the AP exam.
Who is the intended audience for this video?
-The intended audience for this video is students preparing for the AP Calculus AB and BC exams, who are looking for a quick and efficient way to review key concepts.
What is the significance of the handouts mentioned in the video?
-The handouts, titled 'AP Calculus Stuff You Must Know Cold,' are significant as they serve as cheat sheets containing all the major theorems and formulas needed for the AP exam, and the video creator used them to compile the review content.
What algebra skills are emphasized as essential for understanding calculus in the video?
-The video emphasizes the importance of knowing the point-slope form, completing the square, long division with rational expressions, and natural log properties as essential algebra skills for understanding calculus.
Why is it important to know the definition of the derivative for the AP exam?
-It is important to know the definition of the derivative because the College Board often asks questions that involve evaluating limits in the form of the definition of the derivative, allowing students to find the derivative at a point to determine the limit's value.
What is the guest method mentioned in the video for solving related rates problems?
-The guest method is a systematic approach to solving related rates problems that involves drawing a diagram, listing given information, identifying the unknown rate, setting up an equation relating all variables, differentiating with respect to time, substituting given values, and stating the answer.
What are the key concepts covered in the video for analyzing the graphs of functions?
-The key concepts covered for analyzing graphs include the increasing/decreasing test, concavity tests, finding critical points, inflection points, and using the first and second derivative tests.
What are some of the optional calculus topics mentioned in the video that might appear on the AP exam?
-Some optional calculus topics mentioned include trigonometric identities, certain derivatives that are not commonly tested, and methods for integration such as integration by parts and by partial fractions.
What is the significance of the fundamental theorem of calculus in the context of the video?
-The fundamental theorem of calculus is significant as it is used to evaluate definite integrals and, more importantly, it establishes that the derivative of an integral of a function is just the function itself, which is a key concept in calculus.
How does the video address the topic of series for AP Calculus BC students?
-For AP Calculus BC students, the video covers common series, convergence tests, Taylor and Maclaurin series, and error bounds, emphasizing the importance of understanding the convergence and manipulation of series.
Outlines
📚 AP Calculus Exam Preparation Overview
The speaker introduces a comprehensive study guide for the AP Calculus exams, highlighting the effort put into creating the video and PowerPoint to compile essential information. The video is aimed at helping students prepare for both AP Calculus AB and BC exams. The speaker thanks the viewers for their support and mentions Sean Byrd's contribution through his handouts titled 'AP Calculus Stuff You Must Know Cold,' which are recommended for additional study material. The speaker emphasizes the importance of the video and the supplementary materials for students who want to excel in calculus.
🔍 Reviewing Prerequisite Skills for AP Calculus
This paragraph delves into the necessary algebra and precalculus skills that students should master before tackling AP Calculus. It covers the point-slope form for linear equations, completing the square, long division, and natural logarithm properties. The speaker also touches on useful precalculus skills such as knowing the values of trigonometric functions for common angles and understanding trigonometric identities, which can simplify problem-solving on the AP exam.
📘 Derivatives and Graph Analysis in AP Calculus
The speaker focuses on the core concept of derivatives, emphasizing the need to understand the definition of a derivative and its application in evaluating limits. L'Hôpital's rule is introduced for indeterminate forms. Basic derivative formulas are listed as essential to memorize, along with derivative rules such as the chain rule, product rule, quotient rule, and the derivative of inverse functions. The paragraph also covers graph analysis, including the increasing/decreasing test, concavity tests, and identifying critical points and inflection points.
📐 Applications of Derivatives in AP Calculus
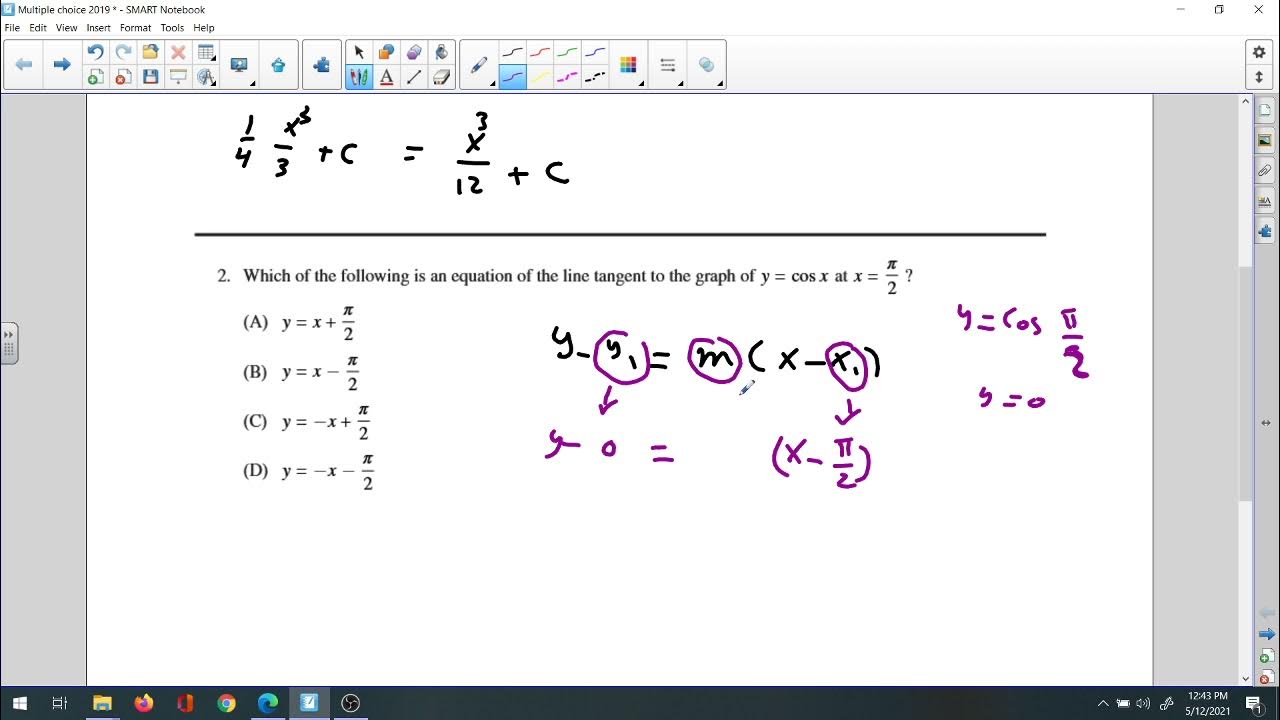
This section discusses various applications of derivatives, including related rates using the guest method, optimization problems, and finding equations of tangent lines. It also touches on linear approximations and the concept of motion, which involves understanding position, velocity, and acceleration. The speaker provides a brief overview of how to approach these problems and the importance of these topics in the AP Calculus exam.
📚 Fundamental Calculus Theorems and Integrals
The speaker explains several fundamental calculus theorems, including the Intermediate Value Theorem, the Mean Value Theorem, and its special case, Rolle's Theorem. The Fundamental Theorem of Calculus is discussed in two parts: evaluating definite integrals and the chain rule for derivatives. The paragraph also covers basic integral formulas and properties that students must memorize, as well as methods and types of integration, such as substitution, long division, completing the square, and using the integral calculus theorems.
📉 Calculus Applications: Area, Length, and Motion
This section covers applications of calculus in determining areas between curves, arc length, and volumes of solids of revolution. It explains the disk method, washer method, and the method for solids with known cross-sections. The paragraph also revisits motion problems, introducing the concepts of speed, distance traveled, and how to find position using both integrals and initial conditions.
🔢 Series and Convergence Tests in AP Calculus BC
The speaker introduces topics specific to AP Calculus BC, starting with series and convergence tests. It outlines common series, geometric series, and their convergence criteria. The paragraph discusses various convergence tests, such as the p-series test, comparison test, divergence test, alternating series test, and the integral test. The importance of the ratio test in determining the convergence of a series is emphasized.
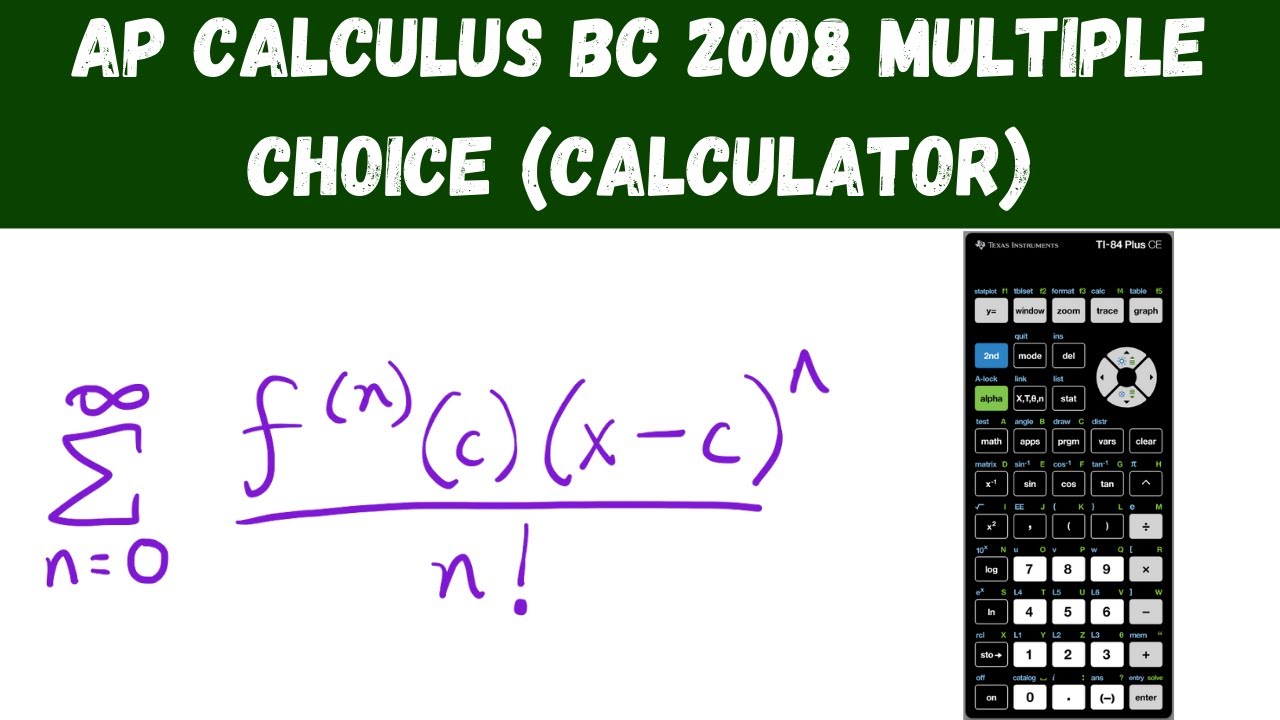
📈 Taylor and Maclaurin Series for Advanced Calculus
This paragraph delves into Taylor and Maclaurin series, explaining how to approximate functions using polynomials based on their derivatives at a given point. It provides the general formula for Taylor series and emphasizes the importance of memorizing and manipulating the first five Maclaurin series. The speaker also touches on the concept of remainder and error bounds when approximating series.
🎓 Final Encouragement and Conclusion for AP Calculus Students
In the concluding remarks, the speaker offers encouragement to students, reminding them not to define their worth by their AP exam scores. They highlight the importance of self-belief and the potential for future success, regardless of exam outcomes. The speaker thanks the viewers for their support and patience throughout the lengthy video, expressing gratitude for their engagement with the content.
Mindmap
Keywords
💡AP Calculus
💡Derivative
💡Integral
💡Limit
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Critical Points
💡Inflection Points
💡Related Rates
💡Optimization
💡Taylor Series
💡Convergence Tests
Highlights
Introduction to the AP Calculus review video, aimed at preparing students for the AP Calculus AB and BC exams.
Special thanks to the viewers for their support and commitment to the channel's educational content.
Acknowledgment of Sean Byrd for his contribution of 'AP Calculus Stuff You Must Know Cold' handouts, which are highly beneficial for exam preparation.
Emphasis on the importance of understanding algebra concepts such as point-slope form and completing the square for calculus success.
Review of precalculus skills including trigonometric functions and identities that are useful for simplifying calculus problems.
Explanation of the definition of the derivative and its significance in evaluating limits, a key concept for the AP exam.
Memorization of basic derivatives is crucial for the AP Calculus exam, with a quick overview provided.
Derivative rules, including the chain rule, product rule, quotient rule, and the rule for derivatives of inverse functions, are discussed.
Analysis of graphs using the first and second derivative tests to find critical points and inflection points.
Introduction to related rates problems and the use of the guest method for solving them efficiently.
Approach to optimization problems using calculus to find maximum and minimum values in applied settings.
Integration techniques overview, including basic integrals that students must memorize for the exam.
Fundamental calculus theorems such as the Intermediate Value Theorem, Mean Value Theorem, and the Fundamental Theorem of Calculus are explained.
Integration methods discussion, including substitution, long division, and completing the square, vital for solving integrals.
Applications of integrals in calculating area between curves, arc length, and volume of solids of revolution.
Motion problems in calculus, relating position, velocity, and acceleration through derivatives and integrals.
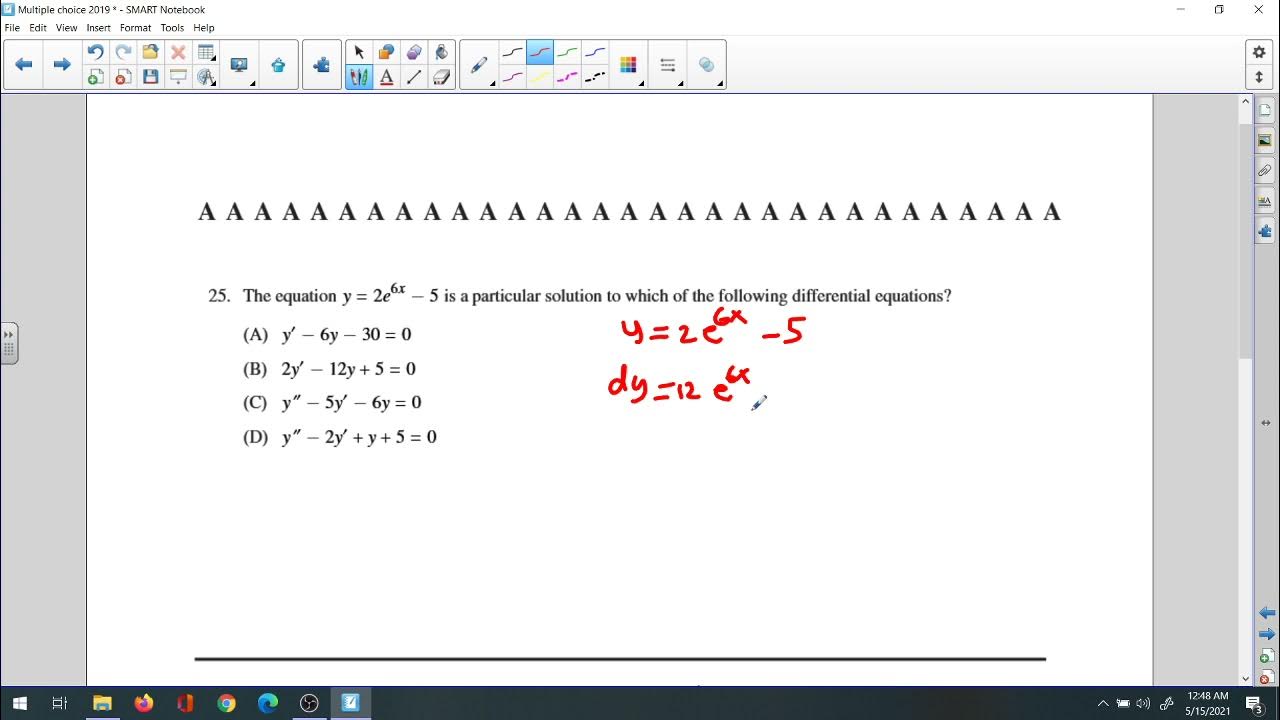
Differential equations and their solutions, including separation of variables and Euler's method.
Series and their convergence tests, an important topic for AP Calculus BC, including p-series and geometric series.
Taylor and Maclaurin series, their applications, and how to manipulate them for the AP exam.
Encouragement and motivation for students not to define themselves by their AP exam scores, emphasizing personal worth and potential.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: