AP Calculus Practice Exam Part 1 (MC #1-10)
TLDRIn this engaging AP calculus class video transcript, the instructor leads students through a practice exam, covering a range of problems from basic integrals to more complex concepts like implicit differentiation and concavity. The session includes humorous interactions and a step-by-step breakdown of each problem, with an emphasis on understanding the underlying calculus principles. The instructor also provides strategies for tackling various types of calculus questions and encourages students to apply these concepts to their exam preparation.
Takeaways
- 📚 The class is reviewing a practice exam for AP Calculus, starting with problem number one, which involves integrating a function.
- 🔍 The instructor demonstrates the process of integration by moving constants outside the integral and finding antiderivatives.
- 📈 In problem two, the class discusses finding the equation of a tangent line by taking the derivative of a function and evaluating it at a given point.
- 📉 The instructor emphasizes the importance of understanding the process behind solving calculus problems, not just memorizing formulas.
- 🤔 The class engages in active problem-solving, with students being called upon to recall and apply calculus concepts such as derivatives and integrals.
- 📝 The transcript includes a detailed walkthrough of a problem involving a chain rule and the derivative of a composite function.
- 🧩 The class uses U-substitution to simplify the integration of a complex function, demonstrating a strategic approach to problem-solving.
- 📉 The instructor explains how to determine the concavity of a function by finding and analyzing the second derivative.
- 🔢 The class practices implicit differentiation, a technique used when the function is not explicitly written in terms of x.
- 📊 The instructor guides the students through finding the area between two curves by setting up and solving an integral.
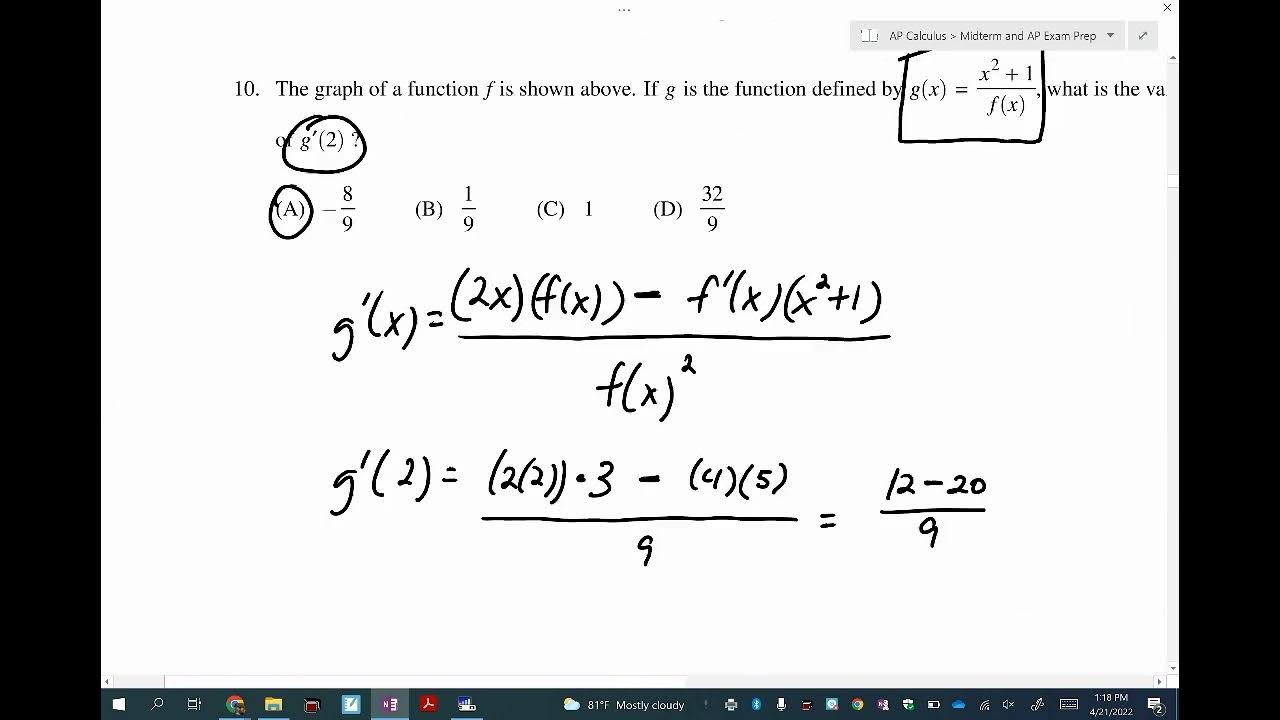
- 📐 The final problem involves using the quotient rule to find the derivative of a function composed of two other functions.
Q & A
What is the integral of x squared over four dx?
-The integral of x squared over four dx is approached by factoring out the constant (1/4) and then integrating x squared, which results in (1/4) * (1/3) * x cubed, plus the constant of integration (C). The final answer is (1/12)x^3 + C.
How do you find the equation of the tangent line to a function at a given point?
-To find the equation of the tangent line, first find the derivative of the function to determine the slope at the given point. Then plug the x-value of the point into the original function to find the corresponding y-value. Use the point-slope form of a line (y - y1 = m(x - x1)) with the slope (m) and the point (x1, y1) to derive the equation.
What is the derivative of cos(x)?
-The derivative of cos(x) with respect to x is -sin(x).
How do you determine the intervals where a function is concave up or concave down?
-To determine the concavity, find the second derivative of the function. Set the second derivative equal to zero and solve for x to find critical points. Then, test intervals created by these critical points by plugging in values into the second derivative. The sign of the result indicates whether the function is concave up (positive) or concave down (negative) in that interval.
What is the process of implicit differentiation?
-Implicit differentiation is used when the equation involves y in a way that is not explicitly in terms of x. It involves differentiating both sides of the equation with respect to x, treating y as a function of x, and then solving for dy/dx.
How do you evaluate dy/dx at a specific point in an implicit differentiation problem?
-After finding the expression for dy/dx through implicit differentiation, plug in the x and y values of the specific point into the expression to evaluate it.
What is the derivative of a^x with respect to x?
-The derivative of a^x with respect to x is a^x * ln(a), where ln(a) is the natural logarithm of the base a.
How do you find the area between two curves?
-To find the area between two curves, determine the points of intersection between the curves. Then, integrate the difference between the two functions over the interval defined by these points.
What is the quotient rule for derivatives?
-The quotient rule states that if you have a function g(x) = u(x) / v(x), then the derivative g'(x) is (v(x) * u'(x) - u(x) * v'(x)) / (v(x))^2.
How do you find the derivative of a function defined as a quotient of two other functions?
-Use the quotient rule to find the derivative of a function that is a quotient of two other functions. Plug in the derivatives of the numerator and denominator and the original functions into the quotient rule formula to find the derivative.
Outlines
📚 AP Calculus Practice Exam Review
The instructor begins an AP Calculus class session by reviewing a practice exam, starting with problem number one, which involves calculating the integral of x squared over four with respect to x. The approach is to factor out the constant, find the antiderivative of x squared, and then apply the constant multiplier. The correct answer is identified as option B, and the process is briefly paused for students to catch up. The instructor then moves on to problem number two, discussing the equation of the tangent line to a function at x equals pi over two, emphasizing the importance of finding the derivative and using the point-slope form of a line equation.
🔍 Derivative and Chain Rule Application
The script continues with an in-depth explanation of how to apply the chain rule to find the derivative of a composite function involving a power and a trigonometric function. The instructor demonstrates the process step by step, from identifying the correct derivative of the inner function to simplifying the expression by combining like terms. Emphasis is placed on the importance of understanding the chain rule for solving complex derivative problems.
🧩 U-Substitution Technique
The third paragraph delves into the concept of U-substitution, a technique used to simplify integrals. The instructor guides the students through the process of identifying the appropriate substitution, transforming the integral, and then finding the antiderivative. The summary includes a detailed walkthrough of the substitution process, the simplification of the integral, and the final evaluation of the integral using the original variable.
📉 Determining Concavity with Second Derivative
In this segment, the focus shifts to analyzing the concavity of a function by finding its second derivative. The instructor explains the steps to determine the intervals where the function is concave up or down, including setting the second derivative equal to zero, factoring, and testing intervals with sample points. The summary highlights the methodical approach to solving such problems and the rationale behind each step.
🔄 Implicit Differentiation Strategy
The instructor introduces implicit differentiation, a technique used when the function is not explicitly expressed in terms of x. The process involves differentiating both sides of the equation with respect to x, rearranging terms, and isolating the derivative of y with respect to x. The summary provides a clear explanation of the steps involved and the reasoning behind them.
📌 Evaluating Derivatives at Specific Points
This part of the script discusses the process of evaluating the derivative of a function at a specific point, which requires implicit differentiation. The instructor demonstrates how to isolate the derivative and then substitute the given point into the derivative to find its value. The summary captures the essence of this process and the importance of correctly applying the differentiation rules.
📚 Review of Derivative Concepts and Limit Evaluation
The script continues with a review of derivative concepts, including the derivative of a function with a base of five raised to the power of x. The instructor also touches on limit evaluation, emphasizing the importance of understanding how to approach limits as x approaches infinity. The summary provides an overview of these concepts and the strategies used to tackle them.
📉 Calculating the Area Between Two Curves
The instructor explains how to calculate the area between two curves, which involves setting the equations of the curves equal to each other to find the points of intersection and then using integral calculus to find the area. The summary outlines the steps taken to graph the curves, determine the intersection points, and calculate the area between them.
📈 Derivative of a Composite Function Using Quotient Rule
The final paragraph of the script focuses on finding the derivative of a composite function defined as the quotient of two functions. The instructor uses the quotient rule to find the derivative and then evaluates it at a specific point given on the graph. The summary encapsulates the method of applying the quotient rule and the process of evaluating the derivative at the given point.
Mindmap
Keywords
💡Integral
💡Antiderivative
💡Derivative
💡Tangent Line
💡Chain Rule
💡U-Substitution
💡Concave Up/Down
💡Implicit Differentiation
💡Quotient Rule
💡Limits
💡Area Between Curves
Highlights
Instructor introduces the practice exam review for AP Calculus class.
Explanation of how to find the integral of x squared over four, including moving constants outside the integral.
Step-by-step breakdown of finding the antiderivative of x squared and multiplying by constants.
Introduction to finding the equation of a tangent line at a given point.
Instructor reviews the derivative of cosine and evaluates it at x equals pi over two.
Explanation of point-slope form and its application to finding the equation of a tangent line.
Discussion of quadrants and radians, including a review of sine and cosine values at key angles.
Introduction to the chain rule for derivatives with a step-by-step example.
Instructor explains the U-substitution method for integrals, demonstrating how to find the antiderivative of a complex function.
Review of concavity and how to determine intervals of concave up and concave down using the second derivative.
Implicit differentiation explained with an example, including moving terms and factoring to isolate dy/dx.
Evaluation of dy/dx at a specific point using implicit differentiation and the steps to simplify the result.
Explanation of evaluating limits as x approaches infinity, focusing on the behavior of functions with exponential growth.
Instructor solves an integral calculus problem to find the area between two curves, demonstrating setting up and evaluating the integral.
Discussion of the quotient rule for derivatives with an example, including finding the derivative of a complex function and evaluating it at a specific point.
Transcripts
Browse More Related Video

AP Calculus Multiple Choice Practice Test (2020 AP CED Problems)

AP Calculus AB/BC Multiple Choice Practice Test (2012 AP CED Problems)

Most Difficult AP Calculus FRQ Parts (Everyone in AB & BC Should Know)

2021 Live Review 8 | AP Calculus AB | Reviewing Multiple-Choice & Free-Response Questions

AP Calc AB & BC Practice MC Review Problems #1
AP Calculus Practice Exam Part 2 (MC #11-20)
5.0 / 5 (0 votes)
Thanks for rating: