AP Calculus Differential Equations Review (All of Unit 7)

turksvids

6 Mar 202133:09

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers a comprehensive review of Unit 7 in AP Calculus, focusing on differential equations. The speaker outlines the importance of understanding differential equations as equations involving derivatives and emphasizes the need to recognize and solve them. The video covers key concepts such as modeling situations with differential equations, including linear and exponential growth. It also delves into verifying solutions, sketching slope fields, and using separation of variables to find general solutions. The speaker provides strategies for solving differential equations and highlights common mistakes to avoid. The script concludes with advice on mastering the topic, recommending the completion of all available practice questions and reviewing additional resources for a deeper understanding.

Takeaways

📚 Differential equations are equations involving derivatives, which can be of any order, and are central to Unit 7 of AP Calculus.
🔗 The course will focus on concepts rather than solving many problems, with links provided for additional examples and practice.
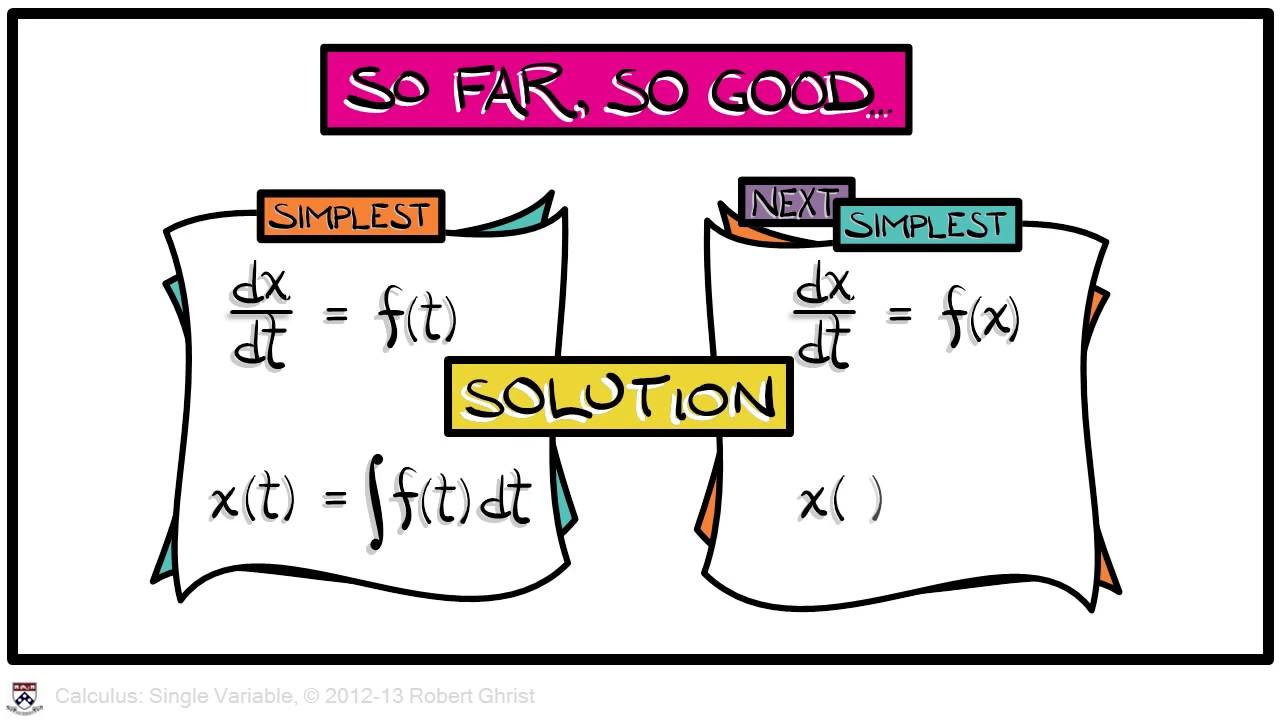
📈 Linear growth is represented by a differential equation where the rate of change of a quantity is constant, such as \( \frac{dp}{dt} = k \).
📊 Exponential growth is characterized by the rate of change of a quantity being proportional to its size, represented by \( \frac{dy}{dx} = k \cdot y \).
🧐 It's crucial to understand the difference between linear and exponential growth when modeling situations with differential equations.
🔍 Verifying solutions involves ensuring the solution is a continuous function that meets the initial conditions and domain of the differential equation.
🤔 For multiple-choice questions, checking the domain and range of the function can help eliminate incorrect options and verify solutions.
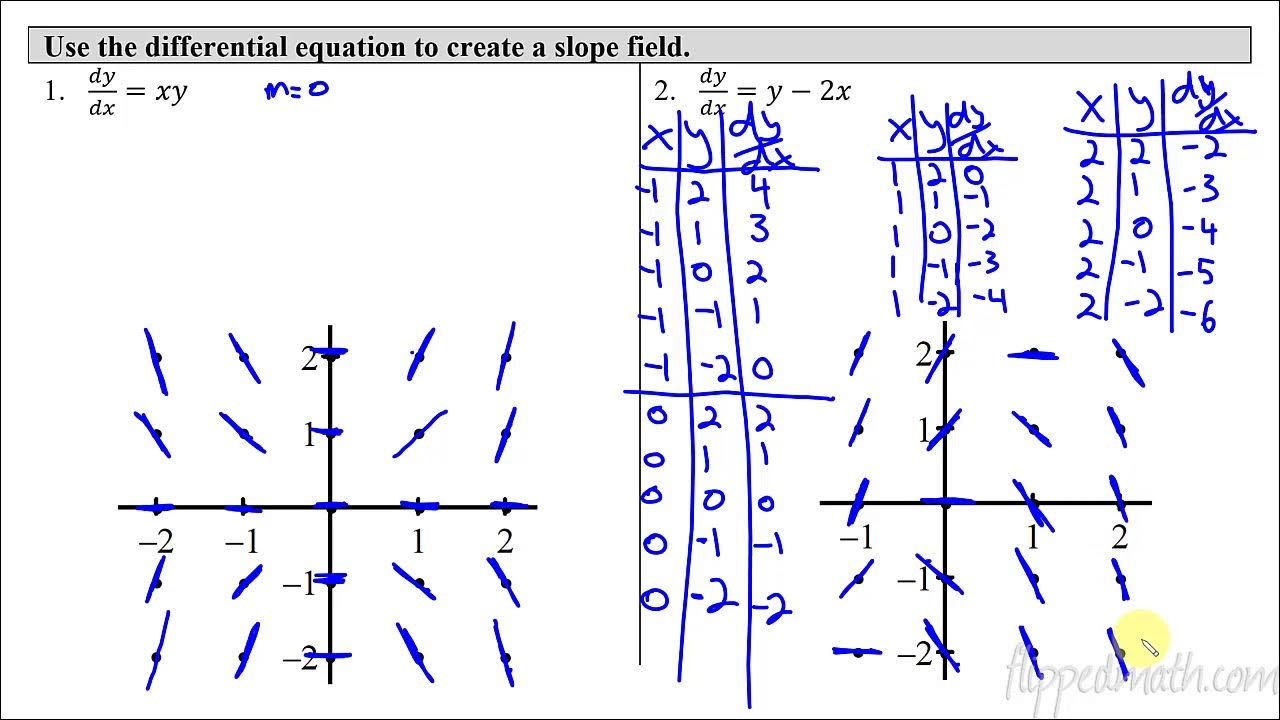
🌐 Slope fields are used to visualize the behavior of solutions to differential equations and can be matched to the equations for analysis.
🖌️ Sketching slope fields involves plotting tangent lines at given points according to the slope, which can be challenging but is an important skill.
✅ To find general solutions using separation of variables, the differential equation must be written as a product of functions of x and functions of y.
⏱️ When solving differential equations, remember to include the constant of integration (+C) and ensure the solution is expressed as an explicit function.
📉 For exponential models, the solution can often be memorized as \( y = y_0 \cdot e^{kx} \), where \( y_0 \) is the initial condition.

Q & A

What is the main focus of Unit 7 in AP Calculus?
-Unit 7 of AP Calculus primarily focuses on differential equations, which are equations that include a derivative.
What does the term 'separable differential equation' refer to?
-A separable differential equation is one that can be written as a product of two functions, one of x and one of y, like dy/dx = f(x)g(y).
How can you identify a differential equation representing linear growth?
-A differential equation represents linear growth when it is of the form dP/dt = k, where k is a constant, indicating the rate of change is constant.
What is the differential equation for exponential growth?
-The differential equation for exponential growth is dy/dx = k*y, where k is a constant and y is the quantity of interest.
What is the importance of verifying solutions for differential equations?
-Verifying solutions is important because it ensures that the proposed solution indeed satisfies the differential equation and the given initial conditions.
How does one find the general solution to a separable differential equation?
-To find the general solution, you separate the variables, integrate both sides, and include a constant of integration (usually denoted as 'C').
What is the role of the initial condition in finding a particular solution to a differential equation?
-The initial condition provides a specific point that the solution must pass through. It is used to solve for the constant of integration, thus determining the particular solution.
Why is it necessary to consider the domain and range when verifying a solution to a differential equation?
-The domain and range must be considered to ensure the solution is valid and continuous on an open interval containing the initial condition. The domain must include the x-value and the range must include the y-value of the initial condition.
What is the general approach to sketching a slope field for a given differential equation?
-The general approach involves plotting points on a grid and drawing tangent lines at those points with slopes corresponding to the differential equation's value at those points.
How can one use a slope field to reason about the behavior of solutions to a differential equation?
-By observing the slope field, one can determine whether solutions are increasing or decreasing, their concavity, and the presence of relative maxima or minima, asymptotes, and other characteristics.
What is the significance of the logistic differential equation in AP Calculus BC?
-The logistic differential equation is a more advanced model of growth that includes carrying capacity, making it a BC only topic. It is used to describe situations where growth is limited by available resources.
What is the advice given for students preparing for the AP Calculus exam?
-The advice includes thoroughly practicing both multiple-choice and free-response questions, understanding the concepts deeply rather than memorizing, and using resources like the instructor's website for additional notes and video explanations.

Outlines

00:00

📚 Introduction to Differential Equations in AP Calculus

The video begins with an introduction to Unit 7 of AP Calculus, focusing on differential equations. The speaker emphasizes that the video will not delve deeply into solving many problems but rather describe concepts and what to expect on the exam. The importance of recognizing differential equations, which include derivatives of any order, is highlighted. The video promises to follow the course description and cover only the AB topics, with a separate video for BC topics to follow. The speaker also mentions that they will provide links to further problems and examples.

05:02

🔗 Linking Concepts with Differential Equations

The speaker explains the process of modeling situations with differential equations, which involves translating verbal descriptions into mathematical equations. Two key types of growth described are linear and exponential growth, each represented by a specific differential equation. The video also discusses how to interpret and apply these equations in various contexts, such as population growth or volume change over time. Strategies for verifying solutions to differential equations are also provided, including checking the domain and range, and ensuring the solution meets the initial conditions.

10:02

🏗️ Constructing and Analyzing Slope Fields

The video moves on to discussing slope fields, which are graphical representations of the instantaneous rate of change of a function. The speaker admits that while computers are better at creating slope fields, understanding how to sketch them manually is important. The process involves plotting points and drawing tangent lines to represent the slope at those points. The video provides tips for sketching slope fields accurately, such as ensuring that the slope is zero where it should be and correctly representing the sign of the slope in different regions of the field.

15:03

🧭 Navigating Slope Fields and Differential Equations

The speaker discusses how to use slope fields to reason about the behavior of solutions to differential equations. This includes matching a given slope field to a differential equation and sketching particular solutions. The video suggests visualizing the slope field as flowing water and tracing the path a leaf would take as it moves through the field. The speaker also recommends watching additional videos on the topic for a deeper understanding of how to match slope fields to differential equations.

20:04

📈 Separation of Variables and General Solutions

The video introduces the method of separation of variables as a technique for solving certain types of differential equations. The speaker explains that a differential equation is separable if it can be written as a product of functions of x and functions of y. The process involves separating the variables, integrating both sides, and solving for the function y. The video also emphasizes the importance of including the constant of integration and ensuring the solution is a valid function that meets the criteria for a solution to a differential equation.

25:04

🎯 Finding Particular Solutions with Initial Conditions

The speaker explains how to find particular solutions to differential equations using initial conditions. This involves solving the general solution for the constant of integration using the given point. The video warns against common mistakes, such as incorrectly applying exponentiation or failing to account for the domain and range of the solution. The speaker also provides tips for solving differential equations, including multiplying by one to simplify equations and factoring out a negative to avoid mistakes in substitution.

30:06

📊 Exponential Models and Differential Equations

The video concludes with a discussion on exponential models in the context of differential equations. The speaker explains the exponential growth differential equation and its solution, emphasizing the importance of memorizing the standard form. The process involves separating variables, integrating, and applying initial conditions to find the constant. The video also mentions that while certain topics like Euler's method and logistic differential equations are BC only, there are resources available for those in the AP Calculus BC course.

Mindmap

Keywords

💡Differential Equation

A differential equation is a mathematical equation that involves a function and its derivatives. It is used to describe the behavior of changing quantities. In the context of the video, differential equations are central to the theme as they are the primary subject of the AP Calculus unit being reviewed. The video discusses various types of differential equations such as linear growth and exponential growth models, emphasizing their importance in mathematical modeling.

💡Separable Differential Equation

A separable differential equation is a type of ordinary differential equation that can be written in the form f(y)dy = g(x)dx, where f is a function of y and g is a function of x. This type of equation is solvable by separating the variables y and x to integrate each side. The video explains that separable differential equations are a key concept in AP Calculus, and it provides examples such as dy/dx = x^2 * y, which can be solved by separating variables and integrating.

💡Exponential Growth

Exponential growth refers to a process where the growth rate of a quantity is proportional to the current size of that quantity. It is often modeled by the differential equation dy/dx = k * y, where k is a constant. The video emphasizes exponential growth as a critical concept in differential equations, showing how it is represented mathematically and how to solve related problems.

💡Initial Condition

An initial condition is a specified value or set of values that determine the unique solution to a differential equation. It is used to find a particular solution that passes through a given point. The video explains that initial conditions are essential in solving differential equations, as they provide the necessary information to solve for the constant of integration.

💡Linear Growth

Linear growth is a type of growth where the rate of change of a quantity is constant. It is represented by the differential equation dp/dt = k, where k is a constant. In the video, linear growth is discussed as a simpler model compared to exponential growth, and the script provides the differential equation that represents this concept.

💡Slope Field

A slope field, also known as a direction field, is a graphical representation that shows the direction and steepness of the slope of a differential equation at various points in the plane. The video discusses slope fields in the context of sketching and analyzing the behavior of solutions to differential equations, noting that they are an important tool for visualizing the solutions.

💡Verification of Solutions

Verification of solutions in the context of differential equations involves checking whether a proposed solution indeed satisfies the differential equation. The video explains that this process is important for confirming the correctness of a solution, typically by substituting the solution back into the differential equation and ensuring the result is an identity.

💡Domain and Range

In the context of functions and differential equations, the domain refers to the set of all possible input values (usually the x-values) for which a function is defined, while the range is the set of all possible output values (usually the y-values). The video emphasizes the importance of considering the domain and range when verifying solutions to differential equations, as the solution must be continuous and defined for the given initial conditions.

💡Accumulation Function

An accumulation function is a way to represent the solution to a differential equation when an explicit antiderivative cannot be found. It involves integrating the rate function over an interval. The video mentions the use of accumulation functions as a valid method to solve certain differential equations, especially when the integral of the rate function does not have a simple closed-form solution.

💡Logistic Differential Equation

The logistic differential equation is a model used in mathematics and biology to describe growth that is limited by available resources. It is a type of differential equation that is BC topic in AP Calculus. The video briefly mentions this equation as part of the more advanced topics covered in AP Calculus BC, which includes modeling growth with limited resources.

💡Euler's Method

Euler's method is a numerical technique used to approximate the solution of a differential equation. It belongs to a class of methods known as iterative methods. The video script mentions Euler's method as a topic covered in AP Calculus BC but does not delve into detail, stating that it will be covered in a different video.

Highlights

The video covers the concepts of Unit 7 of AP Calculus, focusing on differential equations.

Differential equations are equations involving derivatives, which can represent various growth models.

Linear growth is represented by a differential equation where the rate of change is constant.

Exponential growth is characterized by a rate of change proportional to the size of the quantity, with the equation dy/dx = k*y.

Verification of solutions for differential equations is a key topic, requiring checking the domain and range of functions.

The solution to a differential equation must be a function that is continuous on an open interval containing the initial condition.

Sketching slope fields involves creating a visual representation of the slopes of a differential equation at various points.

Slope fields can help in reasoning about the behavior of solutions, such as concavity and extrema.

Separation of variables is a method to solve differential equations by rearranging terms to integrate.

General solutions can be found using separation of variables, and particular solutions can be determined using initial conditions.

When solving differential equations, it's important to consider the domain and range of the resulting function.

Exponential models are significant in differential equations, with a standard form dy/dx = k*y leading to an exponential solution.

Accumulation functions are used when an explicit antiderivative is not available, and they are acceptable solutions in AP Calculus.

The logistic differential equation, covered in AP Calculus BC, models growth with carrying capacity.

The video provides strategies for solving differential equations, including when to use accumulation functions and how to avoid common mistakes.

The presenter recommends watching additional videos and practicing with multiple-choice and free-response questions for thorough preparation.

The video concludes with encouragement and resources for students preparing for AP Calculus exams, emphasizing the importance of practice.

Transcripts

Browse More Related Video

AP Calculus AB/BC Unit 7 Practice Test

Calculus Chapter 3 Lecture 17 Indefinite Integrals

Business Calculus - Math 1329 - Section 5.1 - Indefinite Integration & Differential Equations

Calculus AB/BC – 7.3 Sketching Slope Fields

Lec 1 | MIT 18.03 Differential Equations, Spring 2006

Calculus AB Homework 7.2 Slope Fields

Related Tags

Differential Equations AP Calculus Linear Growth Exponential Growth Solution Verification Separation of Variables Slope Fields Accumulation Functions Educational Review Mathematical Analysis Exam Preparation