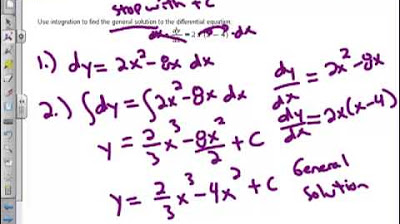Business Calculus - Math 1329 - Section 5.1 - Indefinite Integration & Differential Equations
TLDRThis educational video script delves into the concepts of indefinite integrals, integral equations, and differential equations. It begins by illustrating how different functions can share the same derivative, leading to the introduction of antiderivatives. The script explains the process of finding antiderivatives, or integrating, using various power, logarithmic, and exponential rules. It also covers how to find specific antiderivatives that pass through given points. The video further explores integration by solving for functions that satisfy differential equations, using methods like separation of variables. It discusses general and specific solutions to these equations, including handling initial value problems. Practical applications, such as modeling the sales of a new product or the spread of a disease through the community, are also examined. The script serves as a comprehensive guide for learners to understand the fundamentals of calculus, particularly in the context of integration and differential equations.
Takeaways
- 📈 The derivative of a function can be used to find the slope of the function at different points, which is the same for functions that have the same derivative.
- 🔁 The process of finding a function from its derivative is called antiderivation or integration, and it results in a family of functions called antiderivatives.
- ∞ Every function has infinitely many antiderivatives, which differ by a constant (commonly denoted as + C).
- 🔍 To find a specific antiderivative that passes through a given point, you can use the point's coordinates to solve for the constant in the antiderivative's formula.
- 🧮 Integration is the process of finding antiderivatives and is symbolized by an integral sign, with the integrand and the variable of integration indicated.
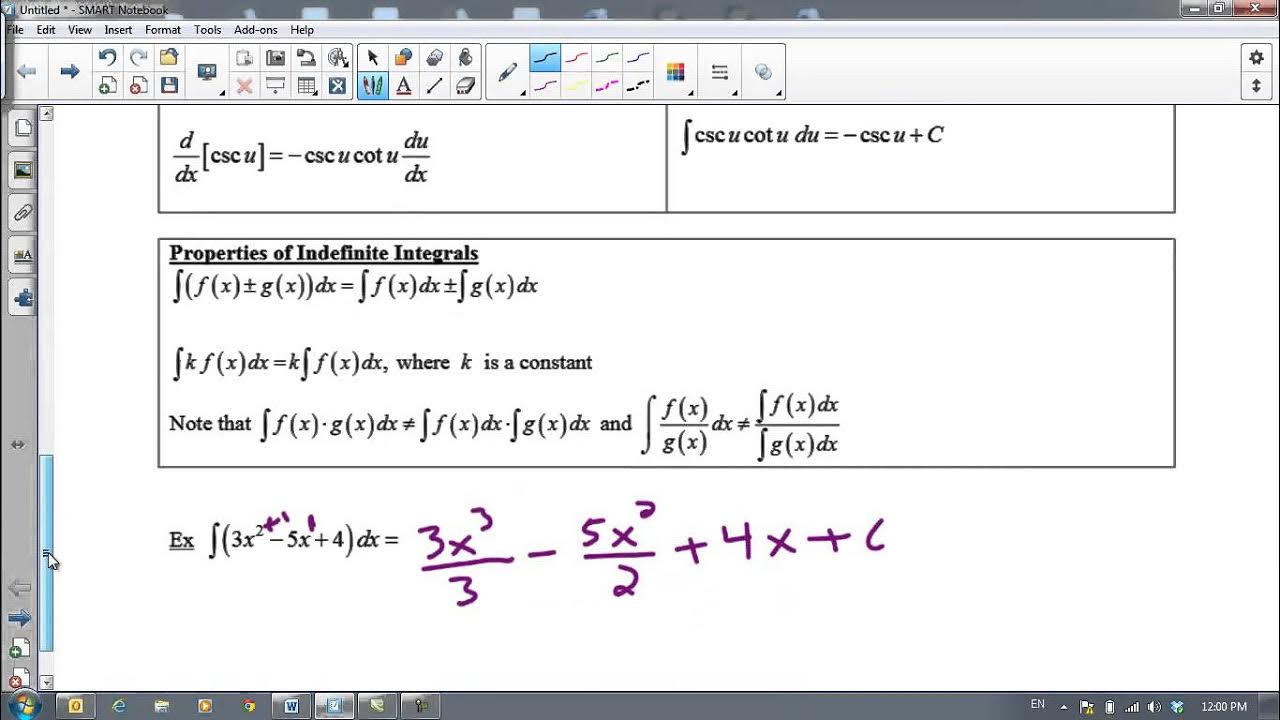
- 📚 Basic integration formulas include the power rule (∫x^n dx = x^(n+1)/(n+1) + C for n ≠ -1), the logarithmic rule (∫1/x dx = ln|x| + C), and the exponential rule (∫e^x dx = e^x + C).
- ✅ Integration can be used to verify an antiderivative by differentiating the result and checking if it matches the original integrand.
- 🛠️ When integrating more complex expressions, terms can be integrated separately, and constants can be factored out.
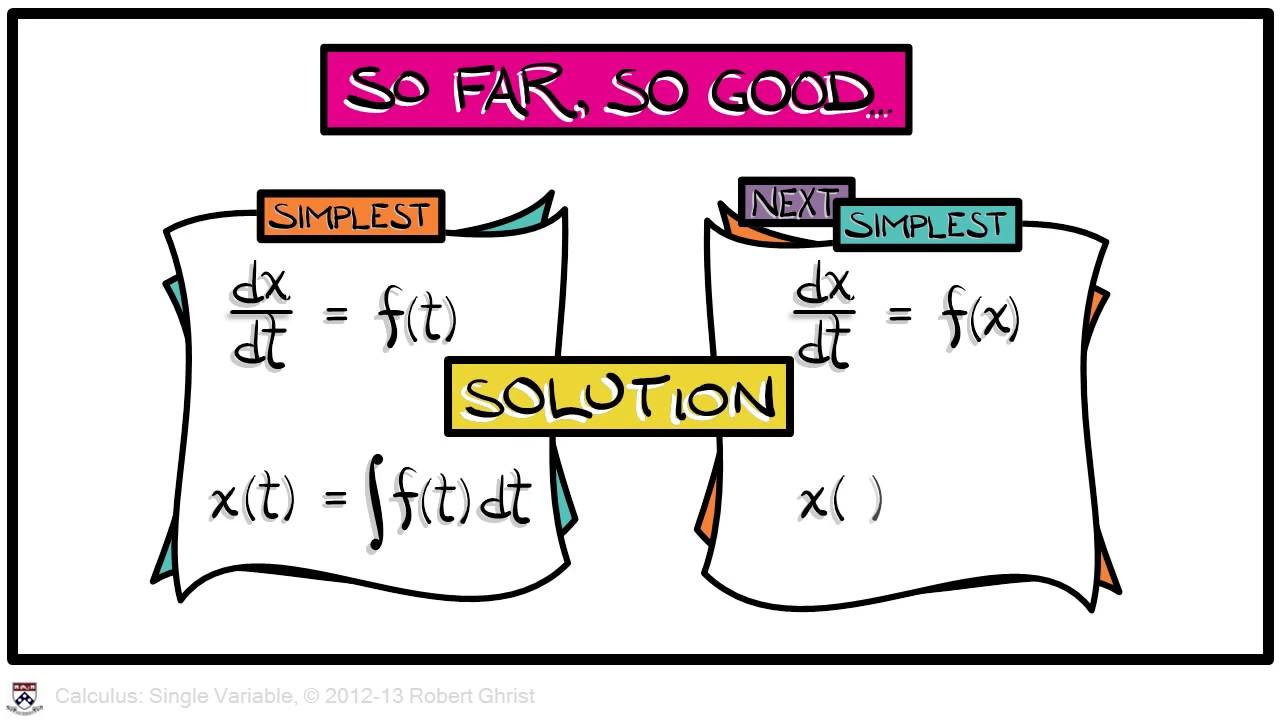
- 🧬 Differential equations involve derivatives and are solved by finding the original function from its rate of change.
- 📌 A specific solution to a differential equation is one that satisfies the equation, and a general solution includes a constant that accounts for all possible solutions.
- 🔑 Initial value problems in differential equations provide an extra condition, usually a point that the solution must pass through, to determine a unique solution.
- 📦 Separation of variables is a common method for solving differential equations, where you isolate variables on opposite sides of the equation before integrating.
Q & A
What is the derivative of the function f(x) = x^2 + 4?
-The derivative of f(x) = x^2 + 4 is f'(x) = 2x, as the derivative of x^2 is 2x and the derivative of a constant is 0.
What is an antiderivative?
-An antiderivative is a function whose derivative is the given function. It represents a family of functions that differ by a constant (indicated by + C).
How do you find the antiderivative of 3x^2 that passes through the point (2, -1)?
-You would use the general antiderivative of 3x^2, which is x^3 + C, and substitute the point (2, -1) into the antiderivative to solve for the constant C. The specific antiderivative that passes through (2, -1) is F(x) = x^3 - 9.
What is the integral sign in calculus and what does it represent?
-The integral sign is a stylized 'S' and it represents the process of integration, which is the act of finding an antiderivative or the area under a curve.
How is the integral of x^n (where n is not equal to -1) calculated?
-The integral of x^n is calculated using the power rule, which states that the integral of x^n dx is x^(n+1)/(n+1) + C.
What is the integral of 1/x dx?
-The integral of 1/x dx is the natural logarithm of the absolute value of x plus C, which is written as ln|x| + C.
What is the process called when you find the antiderivative of a given function?
-The process is called integration, which is the opposite of differentiation and is used to find the original function from its derivative.
What is a differential equation?
-A differential equation is an equation that involves derivatives or differentials and is used to find the original function when only the rate of change is known.
How do you solve a differential equation with an initial condition?
-You solve a differential equation with an initial condition by first finding the general solution of the differential equation and then using the initial condition to find the specific solution that satisfies the condition.
What is the method used to solve differential equations that can be separated into variables?
-The method used is called separation of variables, where you rearrange the equation so that all instances of one variable are on one side and the other variable on the opposite side, then integrate both sides.
How do you find the total number of units sold over time if the rate of change of monthly sales is given?
-You would integrate the rate of change function over the time period of interest to find the total number of units sold. The integral of the rate function gives you the total function, which represents the cumulative sales over time.
Outlines
📈 Introduction to Indefinite Integrals and Differential Equations
The video begins by introducing the concept of indefinite integrals and their relationship with derivatives. It explains that functions with the same derivative have the same slope and can be represented by the same antiderivative, which is a family of functions differing by a constant. The video also defines the antiderivative as a function whose derivative yields the original function and emphasizes that a function has infinitely many antiderivatives.
🧮 Antiderivatives and the Plus C Notation
The video explains the basics of antiderivatives and the common practice of using 'plus C' to represent the family of all antiderivatives for a given function. It demonstrates how to find a specific antiderivative that passes through a given point by solving for the constant. The process of finding antiderivatives is called integration, and the video provides an overview of the terminology and symbols associated with it.
🔢 Basic Integration Formulas and Examples
The video presents basic integration formulas, including the power rule, logarithmic rule, and the integral of the exponential function. It then works through several examples, showing how to integrate terms individually and combine results, including handling constants and the immediate addition of the plus C after integration steps.
🧲 Integration Techniques: Splitting Fractions and Handling Radicals
The video discusses techniques for integrating more complex functions, such as splitting fractions and handling radicals. It covers how to rewrite radicals in fractional exponent form and apply the appropriate integration rules. The video also demonstrates the process of integrating a function that is a product of different powers of x.
🔍 Differential Equations: Definition and Solving
The concept of differential equations is introduced, explaining that they involve derivatives and are used to find the original function when only the derivative is known. The video provides an example of a function that satisfies a differential equation and differentiates between specific and general solutions. It also touches on initial value problems, which are differential equations with an additional condition.
🌀 Separation of Variables and Solving Differential Equations
The video explains the method of separation of variables to solve differential equations. It demonstrates how to isolate variables on opposite sides and integrate both sides to find the general solution. The process is illustrated with an example involving an initial condition, leading to a specific solution for the given problem.
🛒 Application Problems: Sales and Disease Spread Models
The video concludes with application problems involving the use of differential equations to model real-world scenarios. It shows how to integrate the rate of change to find the original function, as in the case of a new toaster's monthly sales, and how to determine when a certain number of sales will be reached. Another example involves a disease spread model, where the video calculates the number of new infections after a certain number of days and the total number of people infected over time.
Mindmap
Keywords
💡Indefinite Integration
💡Derivative
💡Antiderivatives
💡Integration
💡Differential Equations
💡Separation of Variables
💡Initial Value Problem
💡Power Rule
💡Logarithmic Rule
💡Exponential Functions
💡Constants
Highlights
Exploration of indefinite integrals, integral equations, and differential equations in section 5.1.
Derivative analysis of given functions f(x), g(x), and h(x), all resulting in the same derivative 2x.
Introduction to the concept of antiderivatives and their definition in relation to derivatives.
Explanation that a function can have infinitely many antiderivatives, differing by a constant.
Visual representation of tangent lines for functions at x=1, demonstrating shared slope.
Integration process described, including the integral sign and its relation to summation.
Basic integration formulas presented, including power rule, logarithmic rule, and exponential rule.
Integration by term-by-term method demonstrated with the integral of 2x + 3.
Solution to find the antiderivative of 3x^2 that passes through a specific point (2, -1).
Integration of more complex functions like 4x^3 - e^x, showcasing integration techniques.
Handling of rational functions and their integration, as shown with 1/t - 1/t^2.
Integration of radical functions, such as the cube root of w, converted to fractional exponent form.
Solution of differential equations using separation of variables, as illustrated with dy/dx = -2x.
Concept of initial value problems in differential equations and finding specific solutions.
Application of differential equations to real-world scenarios, such as the rate of change of a new product's monthly sales.
Integration to find the original function from a given rate of change, as shown with a toasters sales problem.
Use of integration to model and solve a disease spread problem, calculating new infections and total infected over time.
Final summary recapping the key concepts and methods of integration and solving differential equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: